本文主要是介绍分布式与一致性协议之Paxos算法(三),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
Paxos算法
兰伯特关于Multi-Paxos的思考
领导者
我们可以通过引入领导者(Leader)节点来解决第一个问题。也就是说将领导者节点作为唯一提议者,如图所示。这样就不存在多个提议者同时提交提案的情况,也就不存在提案冲突的情况了。这里补充一点:在论文中,兰伯特没有说如何选举领导者,需要我们在实现Multi-Paxos算法的时候自己实现。比如Chubby中的主节点(也就是领导者节点)是通过执行Basic Paxos算法进行投票选举产生的,那么如何解决第二个问题,也就是如何优化Basic Paxos执行呢
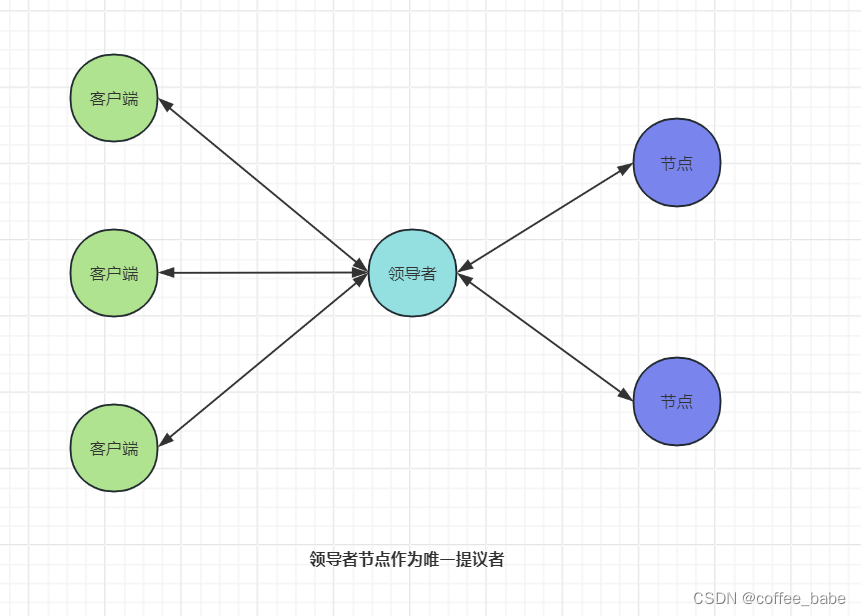
优化Basic Paxos执行过程
我们可以采用"当领导者处于稳定状态时,省掉准备阶段,直接进入接受阶段"这个优化机制,优化Basic Paxos执行过程。也就是说,领导者节点上的序列中的命令是最新的,不再需要通过准备请求来发现之前被大多数节点通过的提案,即领导者可以独立指定提案中的值。这时,领导者在提交命令时,可以省掉准备阶段,直接进入接受阶段,如图所示。
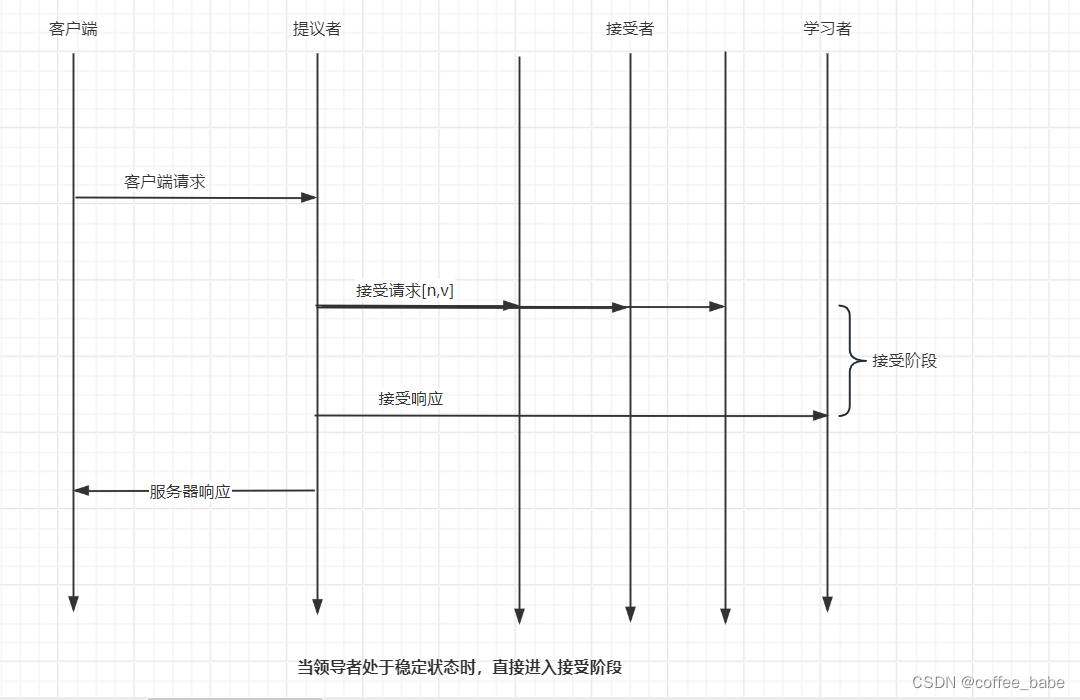
可以看到,与重复执行Basic Paxos相比,当Multi-Paxos引入领导者节点之后,因为只有领导者节点一个提议者,所以不存在提案冲突。另外,当主节点处于稳定状态时,省掉准备阶段,直接进入接受阶段,会在很大程度上减少了往返的消息数,提升了性能,降低了延迟。看到这里你可能会问:在实际系统中,该如何实现Multi-Paxos呢?接下来,接下来以Chubby的Multi-Paxos算法的。
Chubby是如何实现Multi-Paxos算法的
既然兰伯特只是大概地介绍了Multi-Paxos思想,那么Chubby是如何补充细节,实现Multi-Paxos算法的呢?
首先,它通过引入主节点,实现了兰伯特提到地领导者节点地特性。也就是说,主节点作为唯一提议者,这样就不存在多个提议者同时提交提案的情况,也就不存在提案冲突的情况。
另外,在Chubby中,主节点是通过执行Basic Paxos算法进行投票选举产生的,并且在运行过程中,主节点会通过不断续租的方式来延长租期(Lease)。比如在实际场景中,某节点在数天内都是同一个节点作为主节点。如果主节点故障了,那么其他节点会投票选出新的主节点,也就是说主节点一直存在,而且是唯一的。
其次,Chubby实现了兰伯特提到的,"当领导者处于稳定状态时,省掉准备阶段,直接进入接受阶段"这个优化机制。最后,Chubby实现了成员变更(Group Membership),以此来保证在节点变更时集群的平稳运行。
最后,补充一点:在Chubby中,为了实现强一致性,读操作也只能在主节点上执行。也就是说,只要数据写入成功,之后所有的客户端读到的数据将都是一致的。具体过程分析如下。
所有的度请求和写请求都由主节点来处理。当主节点从客户端接收到写请求后,作为提议者,它将执行Basic Paxos实例,将数据发送给所有节点,并在大多数的服务器接收到这个写请求之后,再将响应成功返回给客户端,如图所示。
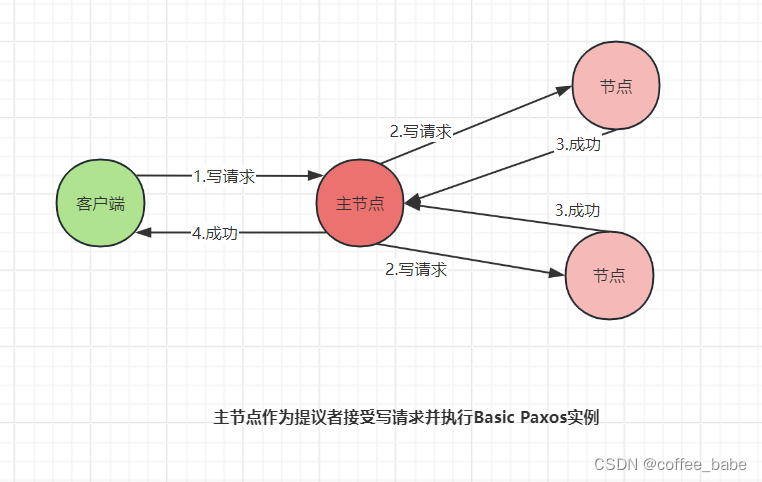
当主节点接收到读请求后,处理就比较简单了。此时,主节点只需要查询本地数据,然后将数据返回给客户端就可以了,
如图所示。
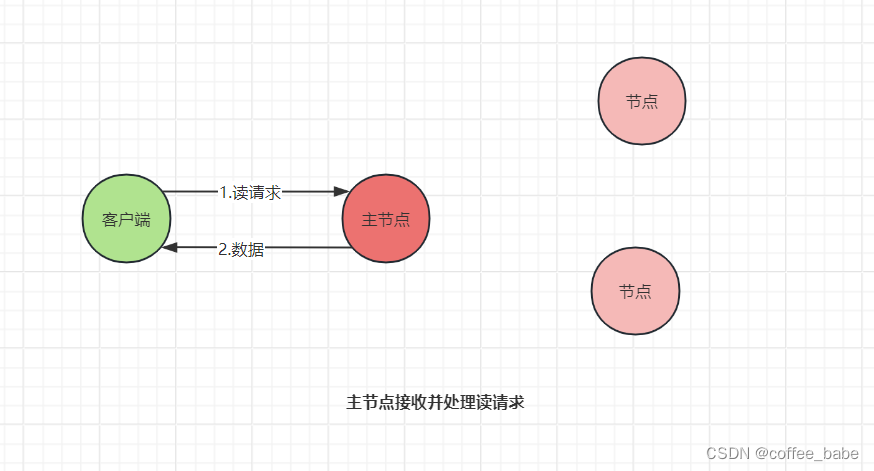
尽管Chubby的Multi-Paxos实现是一个闭源的实现,但这是Multi-Paxos思想在实际场景中的真正落地,Chubby团队不仅
通过编程实现了算法,还探索了如何补充算法论文缺失的必要实现细节。其中的思考和设计非常具有参考价值,不仅能帮助
我们理解Multi-Paxos思想,还能帮助我们理解其他的Multi-Paxos算法(比如Raft算法)
注意
Basic Paxos是经过证明的,而Multi-Paxos是一种思想,缺失实现算法的必须编程细节,这就导致Multi-Paxos的最终算法实现是建立在一个未经证明的基础之上,其正确性有待验证。换句话说,实现Multi-Paxos算法的最大挑战是如何证明它是正确的。
比如Chubby的作者做了大量的测试,运行一致性检测脚本,以验证和观察系统的健壮性。在实际使用时,不推荐设计和实现新的Multi-Paxos算法,而是建议优先考虑Raft算法,因为Raft的正确性是经过证明的。当Raft算法不能满足需求时,再考虑实现和优化Multi-Paxos算法
重点总结
- 1.除了共识,Basic Paxos还实现了容错,即在少于一半的节点出现故障时,集群也能工作。它不像分布式事务算法那样,必须要所有节点都同意后才能提交操作。因为"所有节点都同意"这个原则在出现节点故障的时候会导致整个集群不可用。也就是说,"大多数节点都同意"的原则赋予了
Basic Paxos容错的能力,让它能够容忍少于一半的节点的故障 - 2.Chubby实现了主节点(也就是兰伯特提到的领导者),也实现了兰伯特提到的"当领导者处于稳定状态时,省掉准备阶段,直接进入接受阶段"这个优化机制省掉Basic Paxos的准备阶段,提升了数据的提交效率,但是所有写请求都在主节点处理,限制了集群处理写请求的并发能力,此时其并发能力约等于单机的并发能力
- 3.因为Chubby的Multi-Paxos实现中也约定了"大多数原则",也就是说,只要大多数节点正常运行,集群就能正常工作,所以Chubby能容错(n-1)/2个节点的故障
这篇关于分布式与一致性协议之Paxos算法(三)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









