本文主要是介绍数据结构 - 队列 [动画+代码注释超详解],萌新轻松上手!!!,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一. 队列的概念
队列是一种特殊的线性表,用于存储元素,并且按照先进先出(First In First Out)的顺序进行管理,这意味着最先加入队列的元素将会是最先从队列中被移除的元素
队列的原型:只允许在一端进行插入数据的操作,在另一端进行删除数据的操作
队列的原则:队列中的元素遵循先进先出的原则
队列的两个经典操作:
入队列:队列的插入操作叫做入队列,进行操作的一端称为队尾
出队列:队列的删除操作叫做出队列,进行操作的一端称为队头
二. 队列的结构

现实中的队列
当我们去银行取款机排队取钱的过程就是队列,我们从队尾进入,依次取钱,取完钱之后从队头离开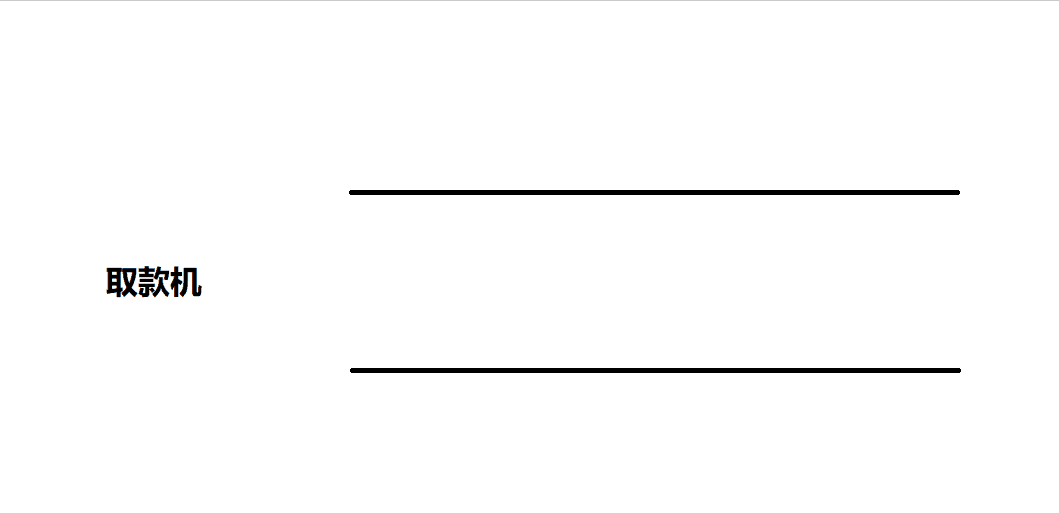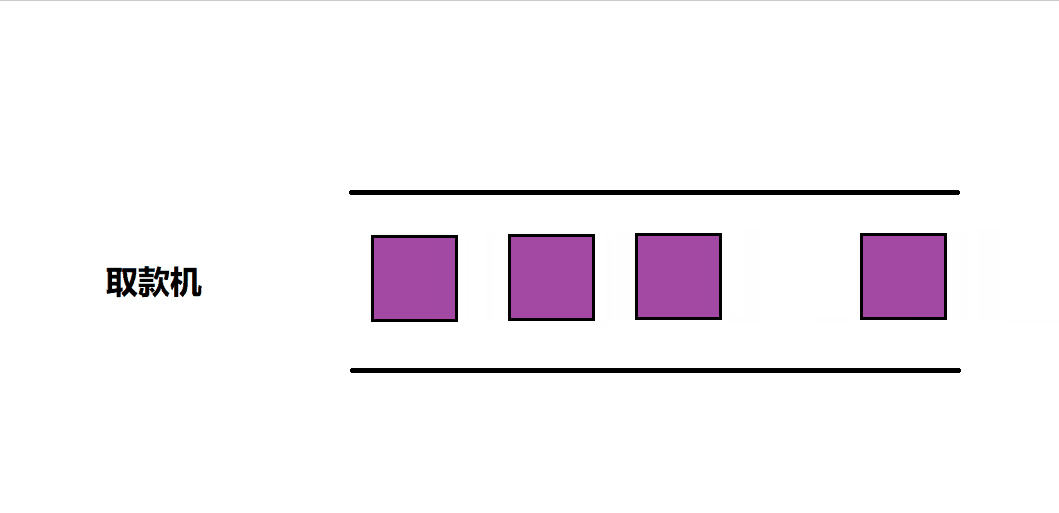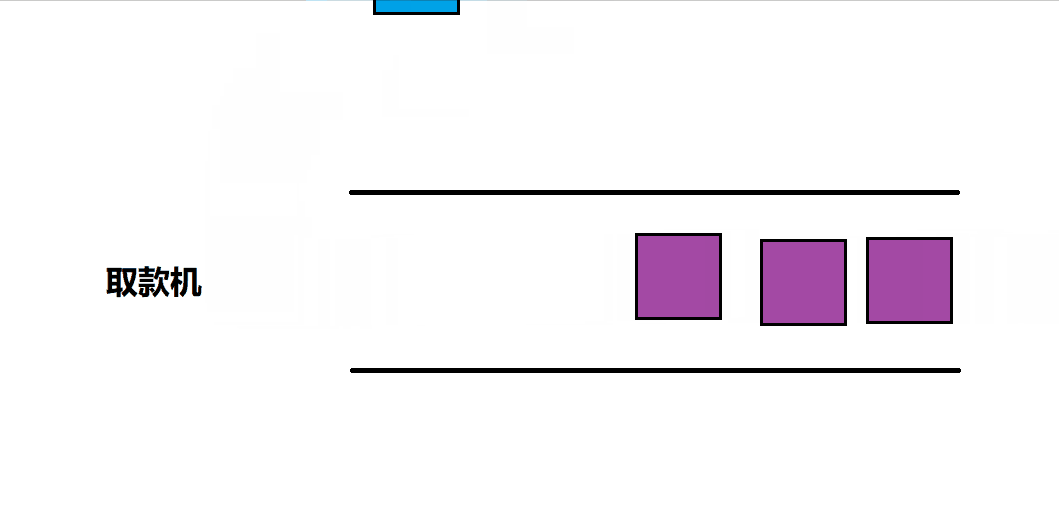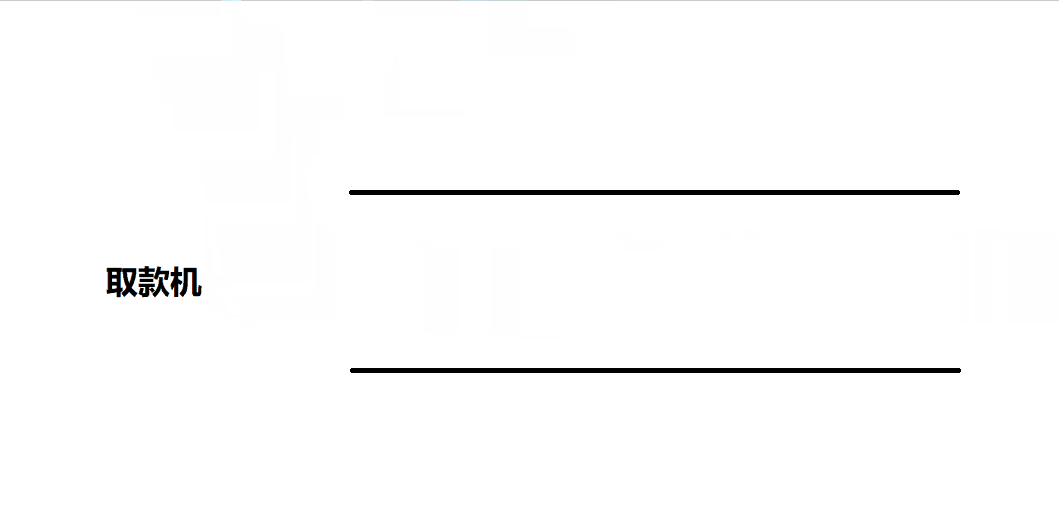
三. 队列的实现
队列的实现有两种方式
一. 用数组实现
优点
- 快速访问:数组允许随机访问,可以快速访问任何一个元素,特别是在入队和出队操作时,可以直接通过索引来访问队头和队尾。
- 内存连续:数组是连续内存的数据结构,这可能有助于提高缓存效率,因为连续的内存块更有可能一起被加载到CPU缓存中。
缺点
- 固定大小:数组的大小在初始化时固定,这意味着队列的容量有一个上限。如果队列满了,就需要执行昂贵的数组扩展操作,通常涉及分配一个更大的数组并复制现有元素。
- 空间浪费:在使用数组实现循环队列时,即使数组中还有空间,队列也可能报告已满,这是因为循环使用的逻辑问题导致的空间利用不充分。
二. 用链表实现
优点
- 动态大小:链表提供了动态大小的能力,队列可以根据需要增长和缩小,不存在固定的容量限制。
- 内存利用率高:链表只在需要时分配内存,且只为实际存储的元素分配,这减少了内存浪费。
缺点
- 内存分配开销:链表的每个新元素都可能需要内存分配(除非使用内存池技术),这可能比连续的内存分配(如数组)更昂贵。
- 访问速度慢:链表不支持随机访问,访问任何位置的元素都需要从头开始遍历,这使得某些操作比数组慢。
- 额外内存需求:每个链表节点需要额外的内存空间来存储指向下一个节点的指针,这增加了每个元素的内存开销。
总结:不过整体上使用链表的结构实现更优一些,因为如果使用数组的结构,出队列在数组头上出数据,效率会比较低。下面我将用链表的结构来实现队列
1. 初始化队列
1.1 链式结构表示队列
在使用链表实现队列的时候,定义一个节点结构QNode,为队列中的每个元素提供一个容器,使得元素能连接起来
typedef int QDataType;typedef struct QListNode //定义一个节点
{struct QListNode* pNext; //指针域QDataType data; //数据域
}QNode;1.2 队列的结构
普通链表通常只需要一个头指针来访问链表的起始位置,而队列为了支持高效的入队和出队操作,需要同时维护队头和队尾两个指针,我们通常会定义一个额外的结构体,这个结构体包括了指向队头的指针和指向队尾的指针。
typedef struct Queue
{QNode* front; // 队头指针QNode* rear; // 队尾指针
} Queue; // 队列结构体别名
1.3 队列的初始化
接下来就是创建一个初始化函数,对队列里的元素进行初始化
void QueueInit(Queue* q)
{assert(q); // 断言队列指针q不为NULL,确保不对NULL指针进行操作,提高程序的安全性。q->front = NULL; // 将队列的前端指针设置为NULL,表示队列为空,即队列中没有元素。q->rear = NULL; // 将队列的后端指针也设置为NULL,与队列为空的状态一致,因为没有元素可以指向。
}
2. 销毁队列
从对头开始,进行释放空间,最后让队头队尾指针置为NULL
void QueueDestory(Queue* q)
{assert(q); // 断言队列指针不为空QNode* cur = q->front; // 创建一个变量,从队头开始销毁队列节点while (cur){QNode* next = cur->next; // 保存当前节点的下一个节点free(cur); // 释放当前节点的内存cur = next; // 移动到下一个节点}q->front = NULL; // 将队列的头指针置为空,表示队列已被销毁q->rear = NULL; // 将队列的尾指针置为空,表示队列已被销毁
}
3. 入队列
申请一个新的节点链接到尾部,然后让尾指针,指向新节点 需要注意的是:若队列中无数据,我们需要让队头和队尾都指向这个新的节点
void QueuePush(Queue* q, QDataType x)
{assert(q); // 断言队列指针不为空QNode* newnode = (QNode*)malloc(sizeof(QNode)); // 分配新节点的内存空间if (newnode == NULL){printf("malloc fail\n"); // 如果内存分配失败,打印错误信息exit(-1); // 退出程序}newnode->data = x; // 将数据存储到新节点中newnode->next = NULL; // 新节点的下一个节点指针为空if (q->front == NULL) // 如果队列为空{q->front = newnode; // 将新节点设置为队列的头节点q->rear = newnode; // 将新节点设置为队列的尾节点}else{q->rear->next = newnode; // 将新节点链接到队列尾部q->rear = newnode; // 更新队列的尾节点为新节点}
}
4. 出队列
释放队头的节点,并将队头更新到下一个元素。需要注意的是,如果队列中只有一个数据,在释放了队头的节点之后,要让队尾和队头的指针置空
void QueuePop(Queue* q)
{assert(q); // 断言以确保队列指针 'q' 不是 NULL,保证这是一个有效的指针。assert(!QueueEmpty(q)); // 断言以确保队列不为空,仅当队列非空时才能进行出队操作。// 如果队列中只有一个节点,即队首和队尾是同一个节点if (q->front->next == NULL){q->front = NULL; // 将队首指针置为空q->rear = NULL; // 将队尾指针置为空,因为队列要变为空队列}else{// 如果队列中不止一个节点,则将队首节点出队QNode* head = q->front->next; // 临时保存新的队首节点free(q->front); // 释放当前的队首节点的内存q->front = head; // 更新队首指针为新的队首节点}
}
5. 获取队列的队头元素
返回队头指针指向的数据即可
QDataType QueueFront(Queue* q)
{assert(q);assert(!QueueEmpty(q));//检测队列是否为空return q->front->data;//返回队头指针指向的数据
}6.获取队列的队尾元素
返回队尾指针指向的数据即可
QDataType QueueBack(Queue* q)
{assert(q);assert(!QueueEmpty(q));//检测队列是否为空return q->rear->data;//返回队尾指针指向的数据
}7. 检测队列是否为空
判断队头的指针是否指向空
bool QueueEmpty(Queue* q)
{assert(q);return q->front == NULL;
}8. 获取队列中有效元素个数
队列中有效元素个数,即队列中的结点个数。我们只需遍历队列,统计队列中的节点数并返回即可
int QueueSize(Queue* q)
{assert(q); // 断言以确保队列指针 'q' 不是 NULL,保证这是一个有效的指针。QNode* cur = q->front; // 创建一个指针 'cur',用来遍历队列,从队首开始int count = 0; // 初始化计数器 'count',用于统计队列中的元素数量// 遍历队列,直到 'cur' 指针为空,即到达队列末尾while (cur){count++; // 对每个节点进行计数cur = cur->next; // 将 'cur' 指针移动到下一个节点}return count; // 返回队列中的元素总数
}
"Yesterday is history, tomorrow is a mystery, but today is a gift. That is why it is called the present."
昨日已成历史,明天充满未知,而今天是一份礼物,这就是为什么它被称为‘现在’。
这篇关于数据结构 - 队列 [动画+代码注释超详解],萌新轻松上手!!!的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





