本文主要是介绍科学高效备考AMC8和AMC10竞赛,吃透2000-2024年1850道真题和解析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
如何在校内学习之余科学、有效地备考AMC8、AMC10美国数学竞赛?多做真题,吃透真题是科学有效的方法之一,通过做真题,可以帮助孩子找到真实竞赛的感觉,而且更加贴近比赛的内容,可以通过真题查漏补缺,更有针对性的补齐知识的短板。
AMC8和AMC10美国数学竞赛的题目广度很广,深度相对一般,对孩子来说更容易建立信心,而且,这些题目吃透了,其背后的知识点、建立的解题思路和方法对校内小学到初中的数学学习也有直接的促进。

我整理了2000-2004年的全部AMC8真题(完整版共600道,且修正了官方发布的原试卷中的少量bug),以及2000-2023年的全部AMC10真题(完整版共1250道),并且全部独家制作成多种在线练习卷,每道题都有详细解析和配套文档、教材。便于孩子利用好碎片化时间,在AMC8竞赛和AMC10竞赛中取得好成绩。
今天我们来看3道AMC8的真题和2道AMC10的真题,并进行详细解析。完整学习资料和信息请查看文末。
2000-2024年AMC8真题和解析:2012年第6题

这道题的考点是代数,列一元一次方程解应用题。
假设最小的数为x,则最大的数为4x,根据题意可得(x+4x)/2=15,解得x=6,所以答案选C。
这道题的关键是理解数轴线上等距排列的含义。如果不理解也可以把各个选项依次代入验算,也可快速得出答案。
2000-2024年AMC8真题和解析:2005第9题
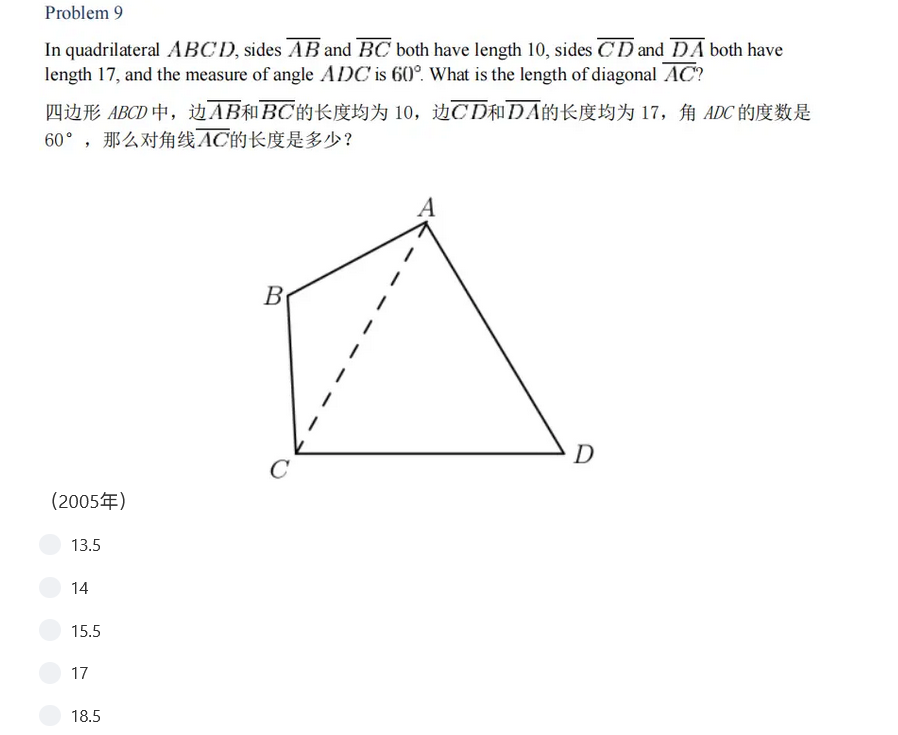
这道题的考点为平面几何,三角形的内角和。
在△ACD中,AD=CD,且∠ADC=60°,可以得出∠CAD=∠ACD=60,因此△ACD为等边三角形。所以AC=DA=17,答案选D。
2000-2024年AMC8真题和解析:2004年第20题

这道题的考点是比例。
首先我们计算椅子数,因为1/4的椅子空着,共6张,所以椅子总数为24张。坐了人的椅子数为3/4*24=18张,即18人坐了椅子,为2/3。所以可得总人数为18/(2/3)=27,答案选D。
2000-2023年AMC10真题和解析:2021年春第18题

这道题的考点是抽象函数。

2000-2023年AMC10真题和解析:2021年秋第8题

这道题的考点是不定方程,分类讨论。
假设这个两位数是AB,则10A+B=B^2+A,即B(B-1)=9A.下面对B的情况进行分类讨论:
1.若B=0,则A=0,不符题意。
1.若B=1,则A=0,不符题意。
2.若B=2,3,4,5,6,7,8时,则A不是整数。
3.若B=9,则A=8,这个两位数是89.
因此只有1个两位数是可爱的,它是89,答案B。
AMC8和AMC10的高质量、科学的备考资源,欢迎了解更多
上述六分成长独家制作的在线练习题,基于认知心理学和教育学原理设计,来源于完整的历年AMC8和AMC10(包括AB卷)真题,并且会持续更新。
这些真题的在线练习除了可以用于参加竞赛备考、反复练习,即使不参加竞赛也可促进小学、初中数学能力提升。还有配套的系统学习文档、视频资料赠送。欢迎联系我了解和获取。
这篇关于科学高效备考AMC8和AMC10竞赛,吃透2000-2024年1850道真题和解析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






