本文主要是介绍西瓜书学习——线性判别分析,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 定义
- LDA的具体步骤
- 1. 计算类内散布矩阵(Within-Class Scatter Matrix)
- 2. 计算类间散布矩阵(Between-Class Scatter Matrix)
- 3. 求解最佳投影向量
- 4. 数据投影
- 5. 分类
定义
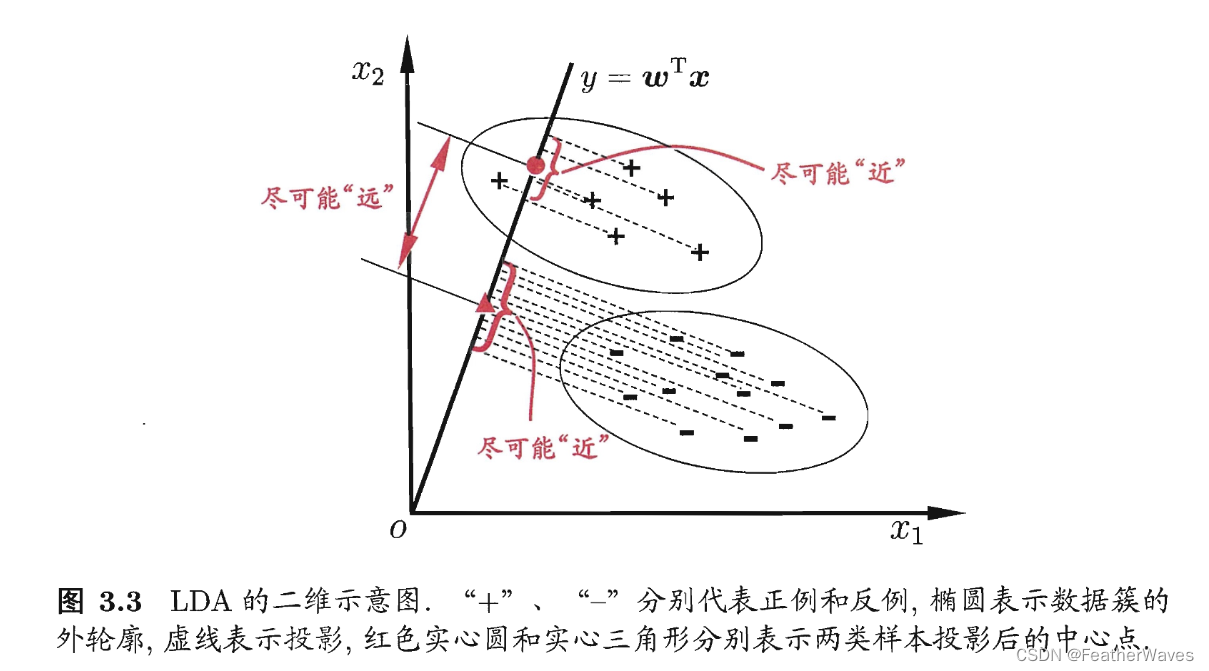
线性判别分析(Linear Discriminant Analysis,简称LDA)是一种常用的监督学习降维技术,主要应用于模式识别和机器学习领域。LDA的核心思想是将高维的数据投影到低维空间,使得投影后的数据在同一类内部尽可能紧凑,不同类之间尽可能分离,从而达到分类的目的。
LDA的具体步骤
1. 计算类内散布矩阵(Within-Class Scatter Matrix)
首先,对于每个类别,我们需要计算其均值和协方差矩阵。假设我们有 K K K 个类别,对于第 k k k 类,其均值向量表示为 μ k \mu_k μk,协方差矩阵表示为 Σ k \Sigma_k Σk。类内散布矩阵 S w S_w Sw可以通过以下公式计算:
S w = ∑ k = 1 K ∑ x ∈ X k ( x − μ k ) ( x − μ k ) T S_w = \sum_{k=1}^{K} \sum_{x \in X_k} (x - \mu_k)(x - \mu_k)^T Sw=k=1∑Kx∈Xk∑(x−μk)(x−μk)T
其中, X k X_k Xk 表示属于第 k k k 类的所有样本。类内散布矩阵反映了同类数据内部的离散程度。
2. 计算类间散布矩阵(Between-Class Scatter Matrix)
类间散布矩阵 S b S_b Sb 可以通过以下公式计算:
S b = ∑ k = 1 K N k ( μ k − μ ) ( μ k − μ ) T S_b = \sum_{k=1}^{K} N_k (\mu_k - \mu)(\mu_k - \mu)^T Sb=k=1∑KNk(μk−μ)(μk−μ)T
其中, N k N_k Nk 是第kk类的样本数量, μ \mu μ 是所有样本的总体均值。类间散布矩阵反映了不同类别数据之间的离散程度。
3. 求解最佳投影向量
LDA 的目标是找到一个投影向量 w w w,使得数据在该向量上的投影能够最大化类间散布与类内散布的比值。这个投影向量可以通过求解下面的最优化问题得到:
max w w T S b w w T S w w \max_w \frac{w^T S_b w}{w^T S_w w} wmaxwTSwwwTSbw
这个最优化问题等价于求解 S w − 1 S b S_w^{-1} S_b Sw−1Sb 的最大特征值对应的特征向量。因此,我们可以通过计算特征值和特征向量来找到最佳的投影向量 w w w。
4. 数据投影
找到最佳投影向量 w w w 后,我们可以将原始数据 x x x 投影到一维空间,得到其在 w w w 方向上的投影:
y = w T x y = w^Tx y=wTx
如果需要进一步降维到多维空间,我们可以找到多个最佳的投影向量,构成一个投影矩阵 W W W,然后通过 y = W T y = W^T y=WT 将数据投影到多维空间。
5. 分类
在降维后的空间中,我们可以使用简单的分类器(如最近邻分类器)进行分类。
这篇关于西瓜书学习——线性判别分析的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






