本文主要是介绍做好A/B测试，需要了解的6个统计学概念，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
做好A/B测试，需要了解的6个统计学概念
A/B测试是一项用来验证产品新功能效果的科学在线测试方法，它能够通过对实际实验数据进行统计分析从而帮助用户做出对产品的不同功能版本进行取舍的决策。为了使A/B测试得到的结论更严谨更科学，我们在AB测试中借助了强大的统计学做理论支持。
我们整理了以下几个基本概念，帮助大家更好地理解A/B测试中的统计学知识：
均值
平均数是反映数据集中趋势的一项指标，一般通过将一组数据集中所有数据之和除以这组数据集的数据个数得到。在A/B测试中，我们无法知道所有用户的行为（如点击率）的真正均值，而只能使用每个抽样样本集的均值。
方差
方差是衡量随机变量或一组数据的离散程度的度量。概率论中方差用来度量随机变量和其数学期望（即均值）之间的偏离程度。当方差越高时，我们预测的平均数偏离真正平均数的可能性就越大，我们采样得到的均值从而可能就越不准确。
抽样
由于我们不可能知道所研究事物总体分布的均值，所以我们不得不在总体分布中进行抽样，从而基于抽样数据进行统计分析。一般来说，我们抽样的样本数越多，方差也会逐渐变小，从而使抽样样本的均值和真正均值的误差降低。
正态分布
又称“高斯分布”，是一个在数学、物理、工程与社会学等领域都非常重要的概率分布，在统计学的许多方面有着重大的影响力。正态分布的概率密度函数曲线呈钟形（两头低，中间高，左右对称），因此又叫钟形曲线。
在进行A/B测试时，有些测试者会直接简单地通过对不同实验版本的指标均值进行比较，从而做出版本之间优劣差异的结果判断。这实际使用了点估计的方法。但是我们需要意识到：
由于样本毕竟有误差，因此点估计的误差也往往比较大。一种更严谨和精确的方法是假设检验的方法，因此专业的A/B测试基本都会选择假设检验来对实验进行判断。
假设检验
又叫显著性检验，是统计学中用来判断从样本得出的结论能否推论到总体的一种方法。一般实验者会提出提出两个假设：一个是“原假设”，另一个是“备择假设”（备选假设）。
其中，“原假设”代表两个样本没有本质区别，而“备择假设”代表两个样本有本质区别。这两个假设互相对立，并且只有一个真正成立。而通过假设检验的分析，我们就能判断出哪个假设有更大的概率成立。在假设检验中，实验者可能犯两类错误：一类错误是指当原假设为真时拒绝了原假设，其概率标记为α(alpha)；二类错误是指当原假设为假时没有拒绝原假设，其概率标记为β(Beta)。
通常来说，犯一类错误的影响会比犯二类错误的大。
置信区间
对于假设检验的结果表达来说，置信区间是一个非常重要的概念。置信区间是指由样本统计量所构造的总体参数的估计区间。在统计学中，一个概率样本的置信区间（Confidence interval）是对这个样本的某个总体参数的区间估计。
置信区间展现的是目标参数的真实值在一定置信水平下落在测量结果附近的范围大小。在A/B测试中，由于我们无法知道真实分布的均值，因此只能通过采样样本进行统计推理，而置信区间便是用来减轻采样误差的风险。置信区间的范围越小，我们的结果往往越精确。
公式如下：
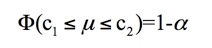
其中α为显著性水平（如0.05或0.1等），而 (1-α)指置信水平。在假设检验分析中，我们可以通过Z分布来计算出累计概率，即得出p-value，然后通过α与p-value的比较，我们可以进一步做出A/B两个版本是否有较大概率存在明显差异的结论。
以上，6个概念，你都了解了吗？
Testin A/B测试服务宣布永久免费，加入我们，一起开启科学增长之路吧：立马免费开始！
这篇关于做好A/B测试，需要了解的6个统计学概念的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
