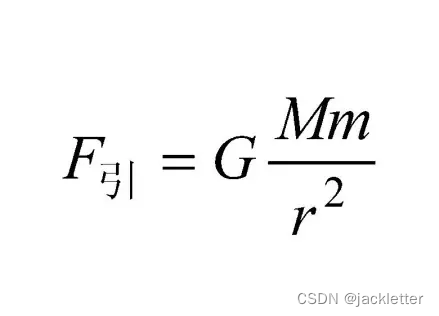融合算法：引力融合

2024-04-25 17:04

文章标签 算法融合引力

本文主要是介绍融合算法：引力融合，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

问题：

有一批数据，如：

[ 1, 2, 3, 45, 46, 55, 89, 101 ]

想把它分成3块，如：

[1, 2, 3]
[45, 46, 55]
[89, 101]

算法：
参考万有引力公式，想象坐标轴上这8个点的分布：
在这里插入图片描述
每一个点都会受到左右其他点的吸引, 引力的大小随着距离的增大而减少, 也随着每个点的质量(点位聚合后，点位质量会增加)而增大。

万有引力公式参考：

这里令G=1, Mm=点位1已聚合的数量*点位2已聚合的数量，r²=两个点位距离的平方，如下示例：
有点 [1, 2, 10, 12]
它们分布如下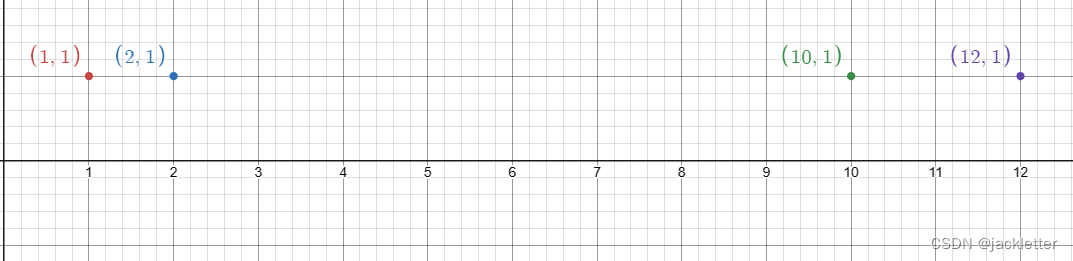：在这里插入图片描述
对于点10来说，它左右的引力为：

 //左
var  leftPower = 1*1/Math.Pow((10-1),2) + 1*1/Math.Pow((10-2),2) ;
//右
var  rightPower = 1*1/Math.Pow((12-10),2);

算出每个点的引力后，再左右引力相抵就知道每个点位被吸引移动的方向和速度了，这可能的结果是：

有的点不动（左右引力正好相抵）；
有的点左移，并计算出速度；
有的点右移，并计算出速度；

这样点位之间的缝隙可能是：

扩大；
缩小，并根据速度计算出缩小直至消失的时间；
不动；

因为是融合，我们关注缩小直至消失的缝隙。
我们从多个缩小的缝隙中找出缩小至不见用时最短的缝隙，然后，让每个点移动它的时间，移动后两个近似的点开始融合，融合后的点位质量+1，循环往复，可以最终得到一个点位，或者是指定融合到某一程度。

实例代码：

var vals = new List<double> { 1, 2, 3, 45, 46, 55, 89, 101 };
var numbers = vals.Select(i => (i, 1)).ToList();
//期望分成3块
while (numbers.Count > 3)
{//进行一次融合numbers = Attract(numbers);
}
//输出结果: numbers

结果如下：
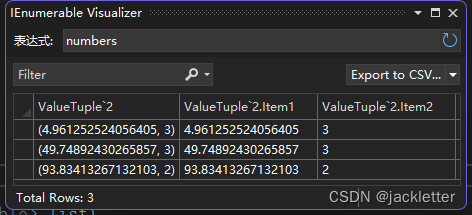
在这里插入图片描述
根据这个结果，不难得出这8个点是怎么分组的。

完整的算法代码：

List<(double value, int count)> Attract(List<(double value, int count)> numbers)
{//1. 先根据引力公式计算每个节点左右的牵引力var powers = new List<(int idx, double leftPower, double rightPower)>();for (int i = 0; i < numbers.Count; i++){//leftvar leftPower = 0d;for (int j = 0; j < i; j++){leftPower += numbers[i].count * numbers[j].count / Math.Pow(numbers[i].value - numbers[j].value, 2);}//rightvar rightPower = 0d;for (int j = i + 1; j < numbers.Count; j++){rightPower += numbers[i].count * numbers[j].count / Math.Pow(numbers[i].value - numbers[j].value, 2);}powers.Add((i, leftPower, rightPower));}//2. 计算每个节点左右移动的向量 value: +向右, -向左List<(int idx, double move)> moveVectors = powers.Select(i => (i.idx, i.rightPower - i.leftPower)).ToList();//3. 计算每个间隙消减的速度和距离 reduce: +减少, -扩大, length: 现有的距离List<(int idx, double reduce, double length)> gapReduce = moveVectors.SkipLast(1).Select((item, idx) => (idx, moveVectors[idx].move - moveVectors[idx + 1].move, numbers[idx + 1].value - numbers[idx].value)).ToList();//4. 计算每个间隙减少完毕需要的时间 得出消减最快的缝隙List<(int idx, double moveTime)> gapTime = gapReduce.Select(i => (i.idx, i.reduce <= 0 ? 0 : i.length / i.reduce)).ToList();var minTime = gapTime.Where(i => i.moveTime > 0).MinBy(i => i.moveTime);//5. 执行消减融合//5.1 先让每个点走相同的时间var newNumbers = moveVectors.Select(i =>{var value = numbers[i.idx].value + moveVectors[i.idx].move * minTime.moveTime;return (value, numbers[i.idx].count);}).ToList();//5.2 检查相近点融合 先得出相消的缝隙插值var tolenrance = Math.Abs(newNumbers[minTime.idx].value - newNumbers[minTime.idx + 1].value);for (int i = 0; i < newNumbers.Count - 1; i++){if (Math.Abs(newNumbers[i].value - newNumbers[i + 1].value) <= tolenrance){//合并/** 1 和 2 发生融合* 0-----------------1-------2-------------------------3* 先插入新的* 0-----------------1(new)-2-------3-------------------------4* 移除 2 和 3, 也就是移除原来的  1 和 2* 0-----------------1-------------------------2* 再从 1 点开始遍历*/var cur = newNumbers[i];var next = newNumbers[i + 1];newNumbers.Insert(i, ((cur.value + next.value) / 2, cur.count + next.count));newNumbers.RemoveAt(i + 2);newNumbers.RemoveAt(i + 1);i--;}}return newNumbers;
}