论文阅读 Graph-Based Global Reasoning Networks

本文主要是介绍论文阅读 Graph-Based Global Reasoning Networks，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

Graph-Based Global Reasoning Networks

论文题目：基于图结构的全局推理网络
会议：CVPR 2018
作者单位：脸书研究院新加坡国立大学
作者： Chen Yunpeng
代码：https://github.com/NUST-Machine-Intelligence-Laboratory/nsrom/tree/main/segmentation/libs

摘要：

区域之间的全局建模和关系推理在完成计算机视觉的任务上有很大的优势。因为卷积神经网络的基础操作Convolution在局部的关系建模较为可观，但是对于远距离的区域即全局关系的建模效率不高，需要通过多个卷积层堆叠来缓解这样的问题。本文提出一种全局推理方法，其中一组特征在坐标空间上全局聚合，然后投影到一个交互空间，并在那里进行有效的计算关系推理。推理过后的关系感知特征分布映射回原始空间坐标，并返回到下一阶段的任务中去。本文进一步提出了一个高效的实例化方法，并引入了全局推理单元。它通过加权全局池和加权广播实现坐标-交互空间映射，以及通过交互空间中小图上的图卷积进行关系推理。我们提出的全局推理单元非常的轻量，能够进行端对端的训练且即插即用。本文也通过大量的实验证明了模块的有效性，囊括了2D乃至3D的卷积任务，包括图像分类，语义分割和视频动作识别任务。

小结：
本文提出了一个GR模型或者叫 GloRe模型。
这个小模块能够对全局的信息进行处理，并且好用，效果也不错。

本文的核心思想：
针对在全输入空间上捕获任意区域之间的关系，本文提出了一种全局推理方法，将坐标空间中彩色区域的特征投影到交互空间中的节点中，形成一个全连通图。在对图进行推理后，节点特征被投影回坐标空间。如下图所示：
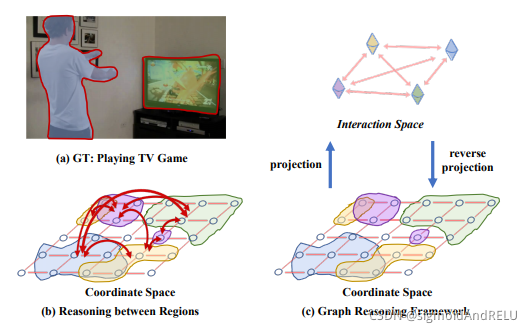
核心思想图

引言：

任意形状的远端区域之间的关系推理在计算机任务中应用广泛。这个问题是这一篇论文以及更多的前面和后续的论文所解决的痛点，总体来说，就是通过构建某个注意力模块来达到对全局信息的把握。我们现有的方法包括通道注意力、空间注意力、多尺度注意力等等，更先进的方法有transformer、LSTM及改进方法等。在这篇论文里，使用全局推理模块来达到类似的效果。
本文的贡献：
1、我们提出了一种新的全局推理方法，即将一组在坐标空间上全局聚合的特征投影到一个交互空间中，从而可以有效地计算关系推理。经过推理后，关系感知特征被分配回坐标空间，用于下游任务。
2、本文提出了全局推理单元(GloRe单元)的一个高效实例化，该方法通过加权全局池化和加权广播实现坐标-交互空间映射，并通过交互空间中的图卷积进行关系推理。
3、在许多数据集上进行了广泛的实验，并表明全局推理单元可以为图像分类、ResNet、ResNeXt、SE-Net和DPN，以及二维和三维CNNs、语义分割和视频动作识别任务。

小结：一个思想，一个思想的实现，可用即可。

方法：

推理单元图：
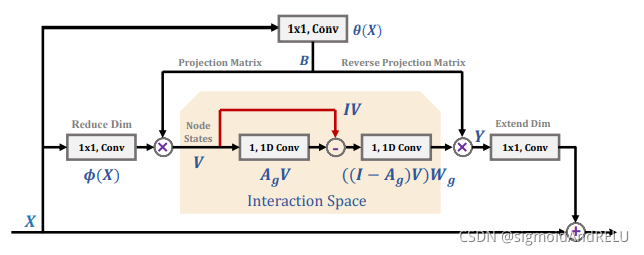
在这里插入图片描述

全局推理单元的体系结构。它包括五个卷积，两个降维和展开（最左边和右边）在输入特征X和输出Y，一个用于生成坐标和潜在交互空间之间的双投影B（顶部），两个基于交互空间的全局推理（中间的）。这里V将区域特征编码为图节点，Wg表示图卷积的参数。

所以这里涉及到几个知识，首先是卷积，这个不用多讲，不懂的同学请自行查阅，再一个是空间投影，最后是图卷积编码。

纵观整个结构，简要的来讲，所有的图形都是2D图像的输入张量，有一张图(V, E, A), 其中V为节点，边E和邻接矩阵A。

全局推理方法概述

本文提出的GloRe单元是用于克服卷积操作的全局建模问题。对于一个特定的输入X， $X∈R^{L×C}$ ，其中C是维度， $L = H \times W$ 。输入标准化使用的是1×1的卷积，可以得到标准化后的梯度矩阵， $Ω=\{1,……，H\}× \{1,……，W\}$ ，即H×W。卷积再有邻接矩阵 $a∈R^{L×L}$ 上进行，如果区域i 与 j 在空间上相邻则 $A_{ij} = 1$ ，否则 $A_{ij} = 0$ 。图的边存储空间相似度，而节点存储位置的特征，具体如图1.C所示。然后，卷积层的输出可以看作是 $Y = A X W$ ，其中W是卷积核的参数，输出 = 图关系 * 输出特征向量 * 参数。因为卷积层能够抓取局部关系，并且有着很好的表现。所以在A，即使用卷积能够很好的提取图A中的局部连接，但对于远距离的关系仍效率低下。
所以有了空间投影的概念。

空间投影：将坐标空间Ω中的特征X投影到隐藏的交互空间 H 中，并化为特征V，其中每一组不相交的区域可以用一个特征表示，而不是用不同位置的一组特征表示。在交互空间H中，我们可以构建一个新的全连通图A，其中每个节点都将新的特征存储为其状态。这样，关系推理简化为对较小图A上节点对之间的交互建模。
一旦我们得到了图A的每个节点的特征，我们就应用一般的图卷积来建立模型和推理每对节点之间的上下文关系。在此之后，我们执行一个反向投影，将得到的特征（用关系信息增强）转换回原始的坐标空间。

那空间映射如何进行?

从坐标空间到交互空间：
第一步，找到目标函数F(), 将原始特征映射到交互空间中，给定一个 $X∈R^{L×C}$ ，要学习这个方法，得到 $V = F(x) ∈ R^{N×C}$ ，N就是图节点的个数，所以有 $V_i = b_iX=\sum_{∀j}{b_{ij}x_j}$ , 学习到的权重 $B=[b_1,……,b_N]∈R^{N×L}, X_j∈R^{1×C}, v_i∈R^{1×C}$ 。
额外说明： $b_i$ 是通过外部数据集训练得到，在这个目标检测的盒子里，如果j在里面则 $b_{ij} = 1$ ，否则 $b_{ij} = 0$ 。本文中的这个 $B_{ij}$ 是用卷积自动生成，而不是是哟个一个额外的检测器。

还就是一遍映射，看了就懂！
使用图卷积进行信息推理
经过上一步的空间映射，远程关系推理也就变成了对应图中节点之间的关系推理。在这里，本文引入了图卷积来处理相应的计算复杂度问题。又是一对定义式：
$Z = GVW_g=((I-A_g)V)W_g$

图卷积的第一步使用拉普拉斯平滑并传播节点特征。在训练过程中，相邻的矩阵学习反映每个节点的底层全局集合特征之间的关系的边缘权值，信息扩散时，每个节点都接收到所有必要的信息，并通过线性变换更新其状态。理解如图所示：
图卷积的应用
信息融合+状态转移，可以说是本文设计的精髓。有兴趣的小伙伴可以仔细查阅代码并进行改造融合到自己的网络结构中去。