本文主要是介绍【题解】NowCoder DP4 最小花费爬楼梯,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
题目来源:牛客
DP4 最小花费爬楼梯
题目描述:
给定一个整数数组 cost , 其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用,下标从 0 开始。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
数据范围:数组长度满足 1 ≤ n ≤ 105 ,数组中的值满足 1 ≤ costi ≤ 104
输入描述:
第一行输入一个正整数 n ,表示数组 cost 的长度。
第二行输入 n 个正整数,表示数组 cost 的值。
输出描述:
输出最低花费。
示例1
输入:3
2 5 20
输出:5
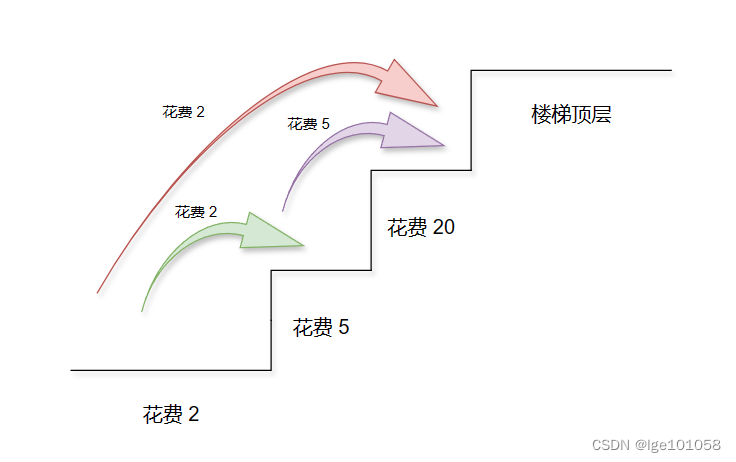
说明:你将从下标为1的台阶开始,支付5 ,向上爬两个台阶,到达楼梯顶部。总花费为5 。
示例2
输入:10
1 100 1 1 1 90 1 1 80 1
输出:6
说明:你将从下标为 0 的台阶开始。
1.支付 1 ,向上爬两个台阶,到达下标为 2 的台阶。
2.支付 1 ,向上爬两个台阶,到达下标为 4 的台阶。
3.支付 1 ,向上爬两个台阶,到达下标为 6 的台阶。
4.支付 1 ,向上爬一个台阶,到达下标为 7 的台阶。
5.支付 1 ,向上爬两个台阶,到达下标为 9 的台阶。
6.支付 1 ,向上爬一个台阶,到达楼梯顶部。
总花费为 6 。
解析
这题很明显的属于动态规划的问题,难度比较简单,只要系统学过动态规划的基本就可以轻松秒杀这题。这题告诉我们,台阶的花费是从该台阶向上爬时的花费,到达该台阶是不需要花费的。我们通过示例可以知道,最后一个台阶并不是楼梯顶部,最后一个台阶上面一层才是。
动态规划最重要的两点就是,①状态表示。②状态转移方程。
其中,状态表示在绝大多数情况下,使 dp表 的每一项数据表示当前情况的最终结果即可。比如说在这一题,我们的 dp[i] 就是到达 i 位置的最小花费,只要令 i 为结果那项的话,dp[i] 就是最终答案。
状态转移方程每一题都不同,需要分析。在这题里面,题目告诉我们,爬楼梯只能每次爬一个台阶或者两个台阶,因此,任意一层台阶只跟上一层和上一层的上一层有关。第 i 层只能通过第 i-1 层或者第 i-2 层到达,且走花费最小的那条路。所以我们能够推算出:dp[i] 就是 dp[i - 1] + cost[i - 1] (选择走上一台阶走一步到达)与 dp[i - 2] + cost[i - 2] (选择走上一个台阶的上一个台阶走两步到达)之间的最小值。
代码实现
#include<iostream>
using namespace std;const int N = 1e5 + 10;
int dp[N], cost[N];
int n;int main()
{cin >> n;for (int i = 0; i < n; ++i){cin >> cost[i];}// 由于向上爬楼梯才有花费,而我们可以直接选择从 0 或 1 开始dp[0] = 0;// 则到达第 0 层和第 1 层是不需要花费的dp[1] = 0;for (int i = 2; i <= n; ++i){// 上一层或上一层的上一层之间的最小值作为新的最小值dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}// 第 n - 1 层是最后一层台阶,n 则是楼梯顶部cout << dp[n];return 0;
}
这篇关于【题解】NowCoder DP4 最小花费爬楼梯的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



