本文主要是介绍面试经典算法系列之数组/字符串2 -- 多数元素,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
面试经典算法题34-多数元素
LeetCode.169
阿Q技术站
问题描述
给定一个大小为 n 的数组 nums ,返回其中的多数元素。多数元素是指在数组中出现次数 大于 ⌊ n/2 ⌋ 的元素。
你可以假设数组是非空的,并且给定的数组总是存在多数元素。
示例 1:
输入:nums = [3,2,3]
输出:3
示例 2:
输入:nums = [2,2,1,1,1,2,2]
输出:2
思路
- 初始化候选多数元素
candidate和其出现次数count。 - 遍历数组,对于每个元素:
- 如果
count为0,则将当前元素设为候选多数元素,并将count设为1。 - 否则,如果当前元素等于候选多数元素,则将
count加1,否则将count减1。
- 如果
- 返回候选多数元素
candidate。
图解
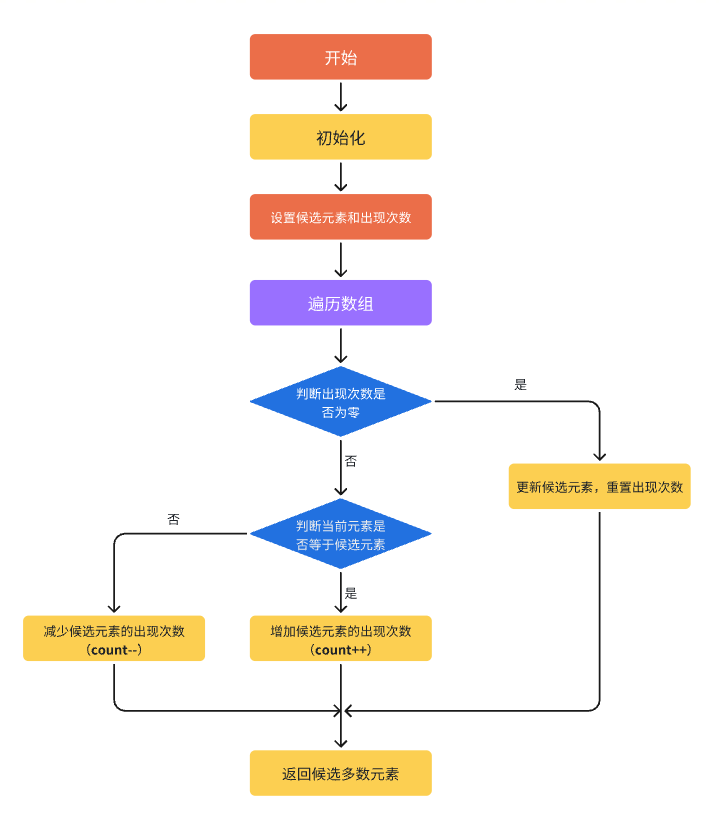
参考代码
C++
#include <iostream>
#include <vector>using namespace std;class Solution {
public:int majorityElement(vector<int>& nums) {int candidate = nums[0]; // 初始化候选多数元素为数组第一个元素int count = 1; // 初始化候选多数元素的出现次数为1// 遍历数组for (int i = 1; i < nums.size(); ++i) {if (count == 0) {candidate = nums[i]; // 更新候选多数元素count = 1; // 重置出现次数为1} else if (nums[i] == candidate) {count++; // 候选多数元素出现,增加出现次数} else {count--; // 候选多数元素未出现,减少出现次数}}return candidate; // 返回候选多数元素}
};int main() {vector<int> nums = {3, 2, 3}; // 输入数组Solution solution;int result = solution.majorityElement(nums); // 查找多数元素cout << "多数元素:" << result << endl; // 输出结果return 0;
}
Java
import java.util.*;class Solution {public int majorityElement(int[] nums) {int candidate = nums[0]; // 初始化候选多数元素为数组第一个元素int count = 1; // 初始化候选多数元素的出现次数为1// 遍历数组for (int i = 1; i < nums.length; ++i) {if (count == 0) {candidate = nums[i]; // 更新候选多数元素count = 1; // 重置出现次数为1} else if (nums[i] == candidate) {count++; // 候选多数元素出现,增加出现次数} else {count--; // 候选多数元素未出现,减少出现次数}}return candidate; // 返回候选多数元素}public static void main(String[] args) {int[] nums = {3, 2, 3}; // 输入数组Solution solution = new Solution();int result = solution.majorityElement(nums); // 查找多数元素System.out.println("多数元素:" + result); // 输出结果}
}
Python
from typing import Listclass Solution:def majorityElement(self, nums: List[int]) -> int:candidate = nums[0] # 初始化候选多数元素为数组第一个元素count = 1 # 初始化候选多数元素的出现次数为1# 遍历数组for i in range(1, len(nums)):if count == 0:candidate = nums[i] # 更新候选多数元素count = 1 # 重置出现次数为1elif nums[i] == candidate:count += 1 # 候选多数元素出现,增加出现次数else:count -= 1 # 候选多数元素未出现,减少出现次数return candidate # 返回候选多数元素# 测试
nums = [3, 2, 3] # 输入数组
solution = Solution()
result = solution.majorityElement(nums) # 查找多数元素
print("多数元素:", result) # 输出结果
这篇关于面试经典算法系列之数组/字符串2 -- 多数元素的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




