UCI手写数字的数据降维

本文主要是介绍UCI手写数字的数据降维，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. 引言

降维是一种常用的数据分析技术，它能够将高维数据转换为低维表示，以便更好地可视化和理解数据。这里我们使用了三种降维方法：主成分分析（PCA）、t-SNE和UMAP，对手写数字图像进行了降维分析。通过比较不同方法的结果，我们评估了它们在保留图像特征的同时减少数据维度方面的效果。

2. 降维算法

PCA：PCA是一种线性降维技术，通过寻找数据中最大方差的方向来进行降维。它通过计算数据的协方差矩阵的特征向量来确定主成分，并将数据投影到这些主成分上。PCA能够保留数据中的主要变化信息，并将其表示为一组新的低维特征。
t-SNE：t-SNE是一种非线性降维方法，它能够在保留样本之间的局部关系的同时，将高维数据映射到低维空间。t-SNE通过计算样本之间的相似度来构建一个高维空间和低维空间之间的映射，使得相似的样本在低维空间中距离更近。
UMAP：UMAP是一种新兴的非线性降维方法，它结合了t-SNE的优点，并通过近邻关系来更好地保留全局结构。UMAP使用了一种基于图的方法，通过构建样本之间的局部连接关系和全局拓扑结构，将高维数据映射到低维空间。

3. 数据降维

我们选择了一个手写数字图像数据集（UCI Optical Recognition of Handwritten Digits Data Set）作为实验数据集，其中包含大量的手写数字图像样本。每个样本都表示为一个高维特征向量。我们的目标是将这些样本映射到二维空间，并比较不同降维方法的效果。

或者使用sklearn的内置函数加载数据集：

from sklearn import datasetsdigits = datasets.load_digits()

步骤如下：

从手写数字图像数据集中选择数字为3（或者全部样本）的样本。
使用PCA、t-SNE和UMAP三种方法对选定的样本进行降维。
将降维后的数据可视化，并根据手写数字的标签进行着色。如果只针对数字3进行降维，则在降维空间中均匀采样25个点并可视化采样点对应的数字3的图像。
比较不同方法的降维结果，评估它们在保留图像特征和可视化效果方面的差异。

4. 降维结果

4.1 数字3的降维结果

图1呈现数字3的降维结果：

PCA：通过应用PCA降维，我们观察到手写数字3在二维空间中呈现出一定的聚类结构。相似的结构往往在降维后的空间中更接近，例如a图中靠降维空间左边区域的3的上半部分会向左倾斜，而越往空间右边的3则呈现向右倾斜的趋势。这说明PCA在保留手写数字图像的整体结构方面具有一定效果。然而，PCA是一种线性降维方法，可能无法捕捉到数据中的非线性关系。
t-SNE：对于t-SNE降维，可以看到3在二维空间中形成了更明显的聚类结构。b图的上半部分空间代表向右倾斜，而下半部分则向左倾斜，同时二者聚类层次比PCA更加明显。这是由于t-SNE能够更好地捕捉到手写数字图像的局部结构和相似性，但可能存在一些过拟合的风险。
UMAP：UMAP综合了t-SNE的优点，能够更好地保持全局结构，并且能够更好地处理数据中的噪声和异常点。相对于t-SNE，UMAP可能在保留整体数据结构方面更具优势。在c图中左侧部分区域为向左倾斜的聚类，右侧为向右倾斜，层次比PCA明显，但仅在数字3上无法体现UMAP和t-SNE之间的降维效果差异。

请添加图片描述

Fig. 1. 数字3的降维结果. a, PCA. b, t-SNE. c, UMAP. 左列为降维散点图, 右列为采样点的图像.

4.2 数字0-9的降维结果

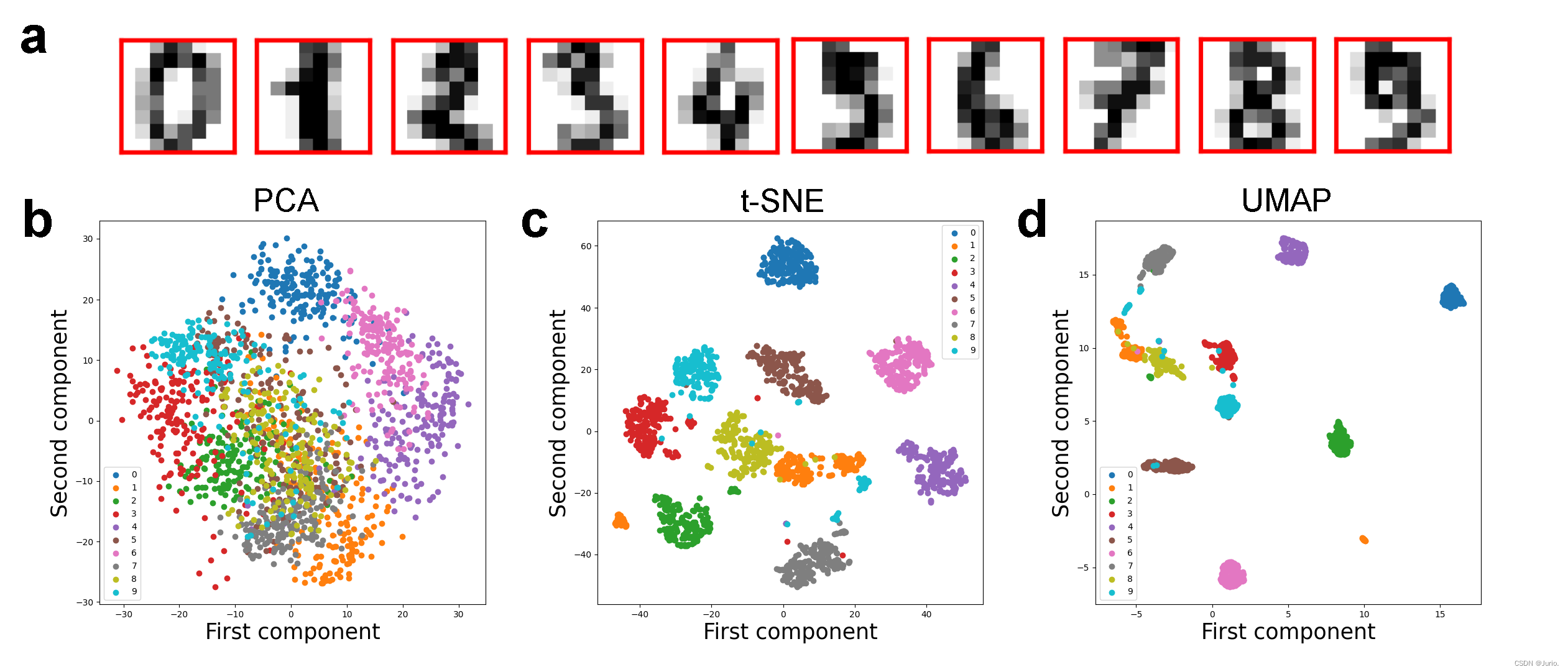
由于仅在数字3上进行降维实验无法观测到不同降维方法之间的显著差异，所以对全部数据0-9进行了降维可视化（图2），进一步突出非线性降维方法在整体数据结构上的优越性。

可以看到与上一节的分析基本一致：PCA作为一种线性降维方法，无法捕捉到数据中的非线性关系，所以在0-9的10类数字的聚类层面没有突出效果，更类似均匀分布。而t-SNE可以捕捉不同数字之间的局部结构差异和相似性，较为清晰地划分出10个类别，同时具有相似笔画结构的数字在降维空间中分布更加靠近，例如1和8（都存在类似从上到下的竖线笔画），还有2、3、5、8和9（都存在从上往下的弧线笔画）等。最后UMAP相较t-SNE的优势在全数字降维上得以体现，不同数字之间的距离进一步扩大，具有相似结构的数字集群之间的距离较小，但和结构差异大的集群之间距离极大，这进一步体现了手写数字的整体数据结构；同时异常点比t-SNE更少，说明UMAP降维效果更加鲁棒。

请添加图片描述

Fig. 2. 数字0-9的降维结果. a, 数字0-9. b, PCA. c, t-SNE. d, UMAP.

from sklearn.manifold import TSNE
from sklearn.decomposition import PCA
from umap.umap_ import UMAPmethod = ['pca', 'tsne', 'umap']
m = method[1]# 获取数字为3的图片索引
digit_3_indices = np.where(digits.target == 3)[0]# 提取数字为3的图片数据
digit_3_images = digits.data[digit_3_indices]if m == 'pca':# 对数字为3的图片进行PCA降维pca = PCA(n_components=2)result = pca.fit_transform(digit_3_images)# 寻找二维平面上分布呈5x5矩阵样子的25个点min_x, max_x = -15, 20min_y, max_y = -15, 20elif m == 'tsne':# 使用 t-SNE 进行降维和可视化tsne = TSNE(n_components=2, random_state=42)result = tsne.fit_transform(digit_3_images)min_x, max_x = -5, 5min_y, max_y = -10, 10else:# 使用 UMAP 进行降维和可视化result = UMAP(n_neighbors=20, n_components=2, random_state=42).fit_transform(digit_3_images)min_x, max_x = -1, 5min_y, max_y = 13, 15x_coords = np.linspace(min_x, max_x, num=5)
y_coords = np.linspace(min_y, max_y, num=5)selected_indices = []
for y in y_coords:for x in x_coords:dist = np.linalg.norm(result - np.array([x, y]), axis=1)closest_idx = np.argmin(dist)selected_indices.append(closest_idx)selected_indices = np.array(selected_indices)# 绘制左子图，所有3可视化为绿色点
fig1 = plt.figure(figsize=(8, 8))
plt.scatter(result[:, 0], result[:, 1], c='green')
plt.scatter(result[selected_indices, 0], result[selected_indices, 1], color='red', marker='o', facecolors='none', linewidth=3, s=200)
plt.xlabel('First component', fontsize=25)
plt.ylabel('Second component', fontsize=25)
plt.savefig(f'./hw2/{m}.png')# 绘制右子图，挑选出来的25个点对应的3的图片按照空间位置绘制成5*5的图片矩阵
fig2 = plt.figure(figsize=(8, 8))
for i, idx in enumerate(selected_indices):ax = plt.subplot(5, 5, i+1)ax.imshow(digits.images[digit_3_indices[idx]], cmap=plt.cm.gray_r, interpolation='nearest')# 设置边框的样式和宽度for spine in ax.spines.values():spine.set_linewidth(3)spine.set_color('red')# 调整子图布局
plt.tight_layout()plt.savefig(f'./hw2/{m}_selected_images.png')# 显示图形
plt.show()