算法刷题day46

本文主要是介绍算法刷题day46，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

引言

今天复习了一下高精度的所有模板，包括加法、减法、乘法、除法，因为自己当时在蓝桥杯的时候没有看出来那个题使用高精度，因为对于一个数的大小和一个数的长度，自己有时候搞不清楚概念，所以当时没看出来，一个数就算是 $long\ long$ 也只有 $18 、 19$ 那么长，所以得记住这个概念。然后就是树形 $D P$ 和状压 $D P$ 了，做了已经很多遍了，已经慢慢的理解了其深层含义，所以还是要先多做题然后才能明白其内涵，以后打算把基础课的题全部刷一遍，好好巩固基础，加油！

一、树的重心

标签：dfs、树形DP

思路：思路就是求每一个结点去除后的最大值，然后在这些最大值里取最小值，如下图所示。这里的 $df s (u)$ 求得是 $u$ 结点的向下的结点个数，我们可以先找到其每个分支的数量，因为删去该结点后，每个分支就是一个连通块，然后向上的一块，也是一个连通块，所以思路就是先对每一个向下的分支的连通块找最小值，然后同时求和，然后用总的结点数一减就是向上的连通块中的结点数，然后再对其求最小值，又因为这是一个递归过程，整个过程是从下往上解决的。然后为什么要建双向边，是因为不知道谁是谁的父节点，也不知道谁是根结点，同时判重，这样就可以只按照一个方向去递归了。

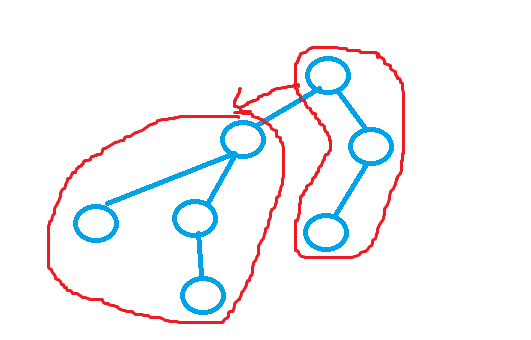
在这里插入图片描述

题目描述：

给定一颗树，树中包含 n 个结点（编号 1∼n）和 n−1 条无向边。请你找到树的重心，并输出将重心删除后，剩余各个连通块中点数的最大值。重心定义：重心是指树中的一个结点，如果将这个点删除后，剩余各个连通块中点数的最大值最小，那么这个节点被称为树的重心。输入格式
第一行包含整数 n，表示树的结点数。接下来 n−1 行，每行包含两个整数 a 和 b，表示点 a 和点 b 之间存在一条边。输出格式
输出一个整数 m，表示将重心删除后，剩余各个连通块中点数的最大值。数据范围
1≤n≤105
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例：
4

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10, M = N * 2, INF = 0x3f3f3f3f;int n, m;
int h[N], e[M], ne[M], idx;
bool st[N];
int ans = 2e9;void add(int a, int b)
{e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}int dfs(int u)  // 找到包括u在内的分支数的和
{st[u] = true;  // 防止往回递归int sum = 1, size = 0;for(int i = h[u]; i != -1; i = ne[i]){int j = e[i];if(st[j]) continue;int t = dfs(j);sum += t;size = max(size, t);}size = max(size, n - sum);ans = min(ans, size);return sum;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);memset(h, -1, sizeof h);cin >> n;for(int i = 0; i < n - 1; ++i){int a, b; cin >> a >> b;add(a,b), add(b,a);  // 因为不知道谁是谁的父节点，也不知道谁是根}dfs(1);cout << ans << endl;return 0;
}

二、毕业旅行问题

标签：状态压缩DP

思路：就是定义一个状态 $f [i] [j]$ 代表从已经走过 $i$ 个城市，走过的城市编号为其二进制的 $1$ 的位数，我们从 $0$ 开始，最终到达 $j$ 号城市的一个集合，那么状态转移方程为先经过 $k$ 号城市，然后再到达 $j$ 号城市，直接按顺序枚举即可。然后初始状态就是只经过 $0$ 号城市，并且最终在该城市，花费为 $0$ ，即 $f [1] [0] = 0$ ，然后只需要判断是否经过 $j, k$ 等城市即可。

题目描述：

小明目前在做一份毕业旅行的规划。打算从北京出发，分别去若干个城市，然后再回到北京，每个城市之间均乘坐高铁，且每个城市只去一次。由于经费有限，小明希望能够通过合理的路线安排尽可能的省些路上的花销。给定一组城市和每对城市之间的火车票的价钱，找到每个城市只访问一次并返回起点的最小车费花销。注意：北京为 1 号城市。输入格式
第一行包含一个正整数 n，表示城市个数。接下来输入一个 n 行 n 列的矩阵，表示城市间的车票价钱。输出格式
输出一个整数，表示最小车费花销。数据范围
1<n≤20,包括北京车票价格均不超过 1000 元。输入样例：
4
0 2 6 5
2 0 4 4
6 4 0 2
5 4 2 0
输出样例：
13
说明
共 4 个城市，城市 1 和城市 1 的车费为 0，城市 1 和城市 2 之间的车费为 2，城市 1 和城市 3 之间的车费为 6，城市 1和城市 4 之间的车费为 5，以此类推。假设任意两个城市之间均有单程票可买，且价格均在 1000 元以内，无需考虑极端情况。

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 20, M = 1 << N;int n, m;
int w[N][N];
int f[M][N];int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);cin >> n;for(int i = 0; i < n; ++i){for(int j = 0; j < n; ++j){cin >> w[i][j];}}memset(f, 0x3f, sizeof f);f[1][0] = 0;for(int i = 1; i < M; i += 2){for(int j = 0; j < n; ++j){if(i >> j & 1){for(int k = 0; k < n; ++k){if(i >> k & 1){f[i][j] = min(f[i][j], f[i-(1<<j)][k] + w[k][j]);}}}}}int res = 2e9;for(int i = 0; i < n; ++i){res = min(res, f[(1<<n)-1][i] + w[i][0]);}cout << res << endl;return 0;
}

三、高精度乘法

标签：高精度、模板题

思路：模板题没什么说的，值得注意的是，这个加法和乘法都涉及到进位，所以这个 $A$ 遍历完了，有时最后刚好进位了，所以也要等 $t$ 为 $0$ 了才行，得判断一下。

题目描述：

给定两个非负整数（不含前导 0） A 和 B，请你计算 A×B 的值。输入格式
共两行，第一行包含整数 A，第二行包含整数 B。输出格式
共一行，包含 A×B 的值。数据范围
1≤A的长度≤100000,0≤B≤10000
输入样例：
2
3
输出样例：
6

示例代码：

#include <bits/stdc++.h>using namespace std;typedef long long LL;
typedef pair<int,int> PII;
#define x first
#define y secondconst int N = 1e5+10;int n, m;vector<int> mul(vector<int>& a, int b)
{vector<int> res;int t = 0;for(int i = 0; i < a.size() || t; ++i){if(i < a.size()) t += b * a[i];res.push_back(t % 10);t /= 10;}while(res.size() > 1 && res.back() == 0) res.pop_back();return res;
}int main()
{ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);string a; int b;cin >> a >> b;vector<int> A;for(int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');auto res = mul(A,b);for(int i = res.size() - 1; i >= 0; --i) cout << res[i];cout << endl;return 0;
}