新国九条下，低波动因子重要性提升！

本文主要是介绍新国九条下，低波动因子重要性提升！，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

之前我们有一期文章介绍了低换手率因子。它的背后的原理是，要买在无人问津处，藏器待时，最终卖在人声鼎沸时。这是一种博弈逻辑。

今天介绍的低波动因子，同样强调无人问津处的价值。由于它的低波动特性，在实操上，不受短线资金青睐；在学术上，它与CAPM、EMH等流行的理论相悖，因而甫一提出，就被华尔街和学术界视为异类。直到2008年，MSCI才开始涉及这一因子，编制了MSCI全球低波动率指数。

大量的实证研究表明， 在长达数十年的投资史中，低波动率因子都具有明显的优势：人迹罕至的道路，有时提供更好的旅程。

新国九条之后，红利股在投资中的重要性将大大加强，而低波动因子在发现红利股、白马股方面有优秀的选择能力。这是我们介绍低波动因子的时间背景。

低波动因子的数据表现

从CAPM模型发表以来，华尔街和学术界坚信风险与回报是紧密相连的：市场是有效的，投资者要获得较高的收益，就必须承担更多的风险。

然而，Robert Haugen和他的老师 James Heins 教授在60~70年代就发现，与流行的理论相反，低风险股票实际上能产生更高的回报。

Haugen认为，有关投资和公司金融的重要教科书“大错特错，需要重写”。由于Haugen对低波动因子的大力推崇，从而获得了“低波动性投资之父”的非正式称号。

根据S&P Global的Tim Edwards博士等人的研究，低波动性指数的风险调整回报在多个国家的表现都超过了母指数，在日本甚至超出近一倍。这个对比图我们不放了，放一个累积收益对比图。

数据来源于S&P Dow Jones Indices, 1990~2018

这个图是低波动因子标的池与市场（标普500）历史累积回报相对比的一个图。从图中可以看出，几乎在任何一个时期，低波动因子的总体收益（而不仅仅是风险调整收益）都超过了市场表现。

他们的构建方法是，从标普500中，挑出波动率最低的20%，并按与波动率成反比的方式进行加权，并且每季度进行一次调仓。

这份研究报告是教育性质的，在jieyu.ai 上提供了免费下载。

MSCI在去年三季度的一篇文章中，披露了他们构建的低波动性指数的表现情况：

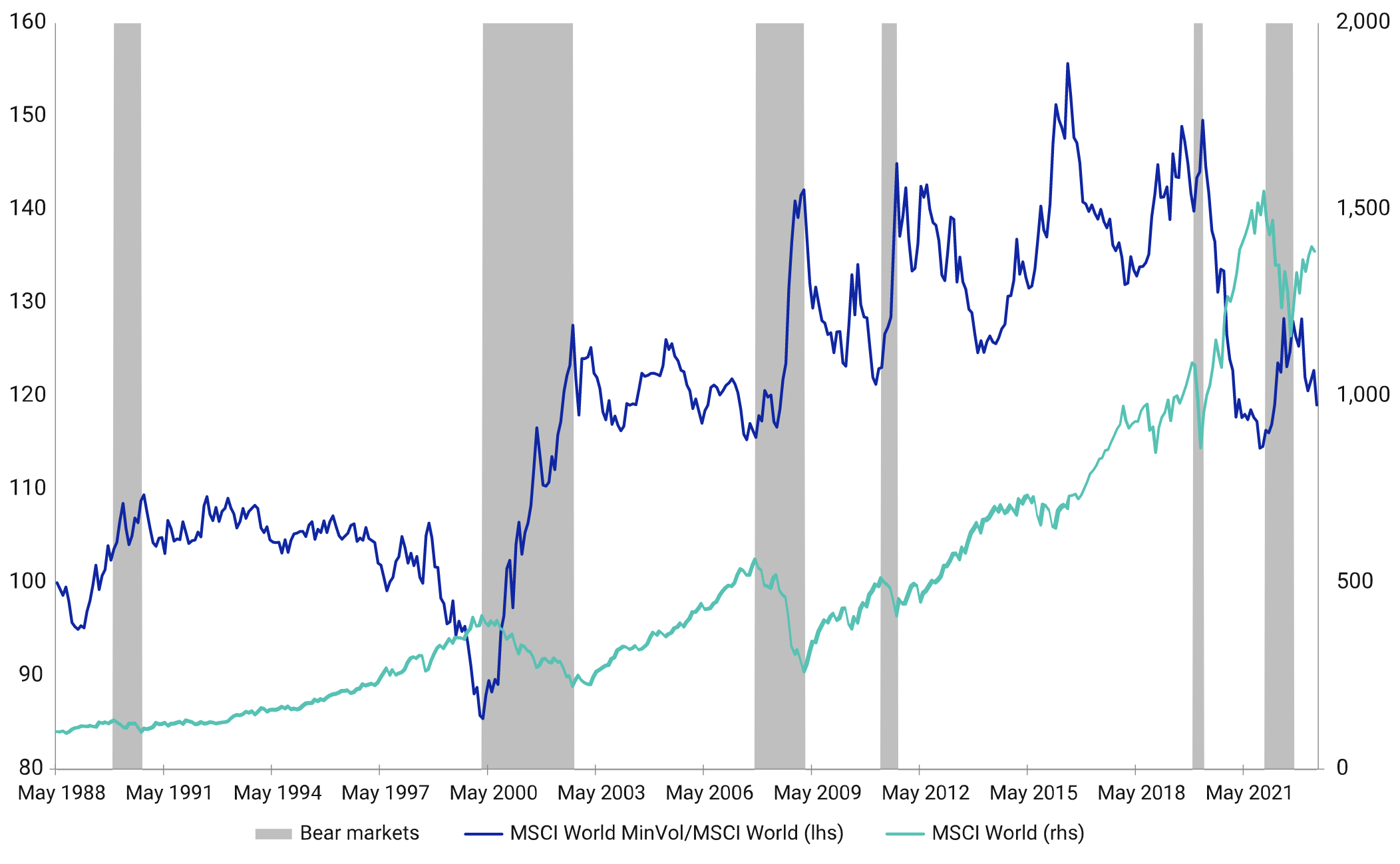
图表来源：MSCI网站

上图显示出，低波动因子在市场衰退期反而能逆市上涨，其它多数时间也跑赢指数。

低波动因子的有效性解释

关于低波动性因子有效的原因，学界也是用了很多数学和数据来解释。但实际上，回到问题的本原上来，低波动性是如何造成的？是由于它的投资者长期看好公司，并且以持有吃分红为主，很少交易造成的。

投资者为什么会长期看好一支股票呢？是因为这些公司的业务逻辑很简单（能看懂，所以投资者不会反反复复）、护城河深（竞争格局很难改变）、盈利足够好（核心还是要能赚钱），是那些世界无法改变的公司（摘自但斌近期路演）。

这就有点价值投资的味道了。实际上，学界有人做了很多研究，最后发现，低波动因子与价值因子有较强的关联性：低波动性的股票、往往也是低市净率的股票。因此，白马股、长期红利股，也往往是低波动率的个股。

一个有趣的事实是，夏普率与波动率的关系。夏普率是一种风险调整收益率，它的分母–资产收益的标准差，正是波动率的线性函数。

夏普率的提出者，正是CAPM理论的创始人威廉.夏普。而低波动率投资方法的支持者们，正是用低波动率作为武器，举起了反抗以CAPM为代表的现代金融理论的旗帜。如此说来，夏普在发表CAPM模型时，也为这一理论安排了自己的掘墓人。这很辩证法。

波动率的计算

根据investopedia，波动率的公式是:

$$vol=\sqrt{var(R)}/T$$

这里的T是产生回报率R的周期数。但也有不除以T的做法。

在金融领域，波动率常以年化方式进行呈现和比较。这可以用pandas来计算:

bars = ...
close = bars["close"]close.pct_change().rolling(window_size).std() * (252**0.5)

在进行单因子检验时，我们需要求得每一天的标的的波动率，因此会需要这里的rolling版本。

或者，更简单地，使用quantpian的开源库empyrical:

from empyrical import annual_volatilitydaily_returns = close.pct_change()
annual_volatility

低波动率策略

一般而言，我们无须自行检验低波动率因子的有效性，可以直接使用它来进行选股。

要注意的是，如果我们以短期的波动率进行选股，非常有可能选中下跌状态中的个股。下图显示了相同的波动率，可以出现完全不同的股价走势：

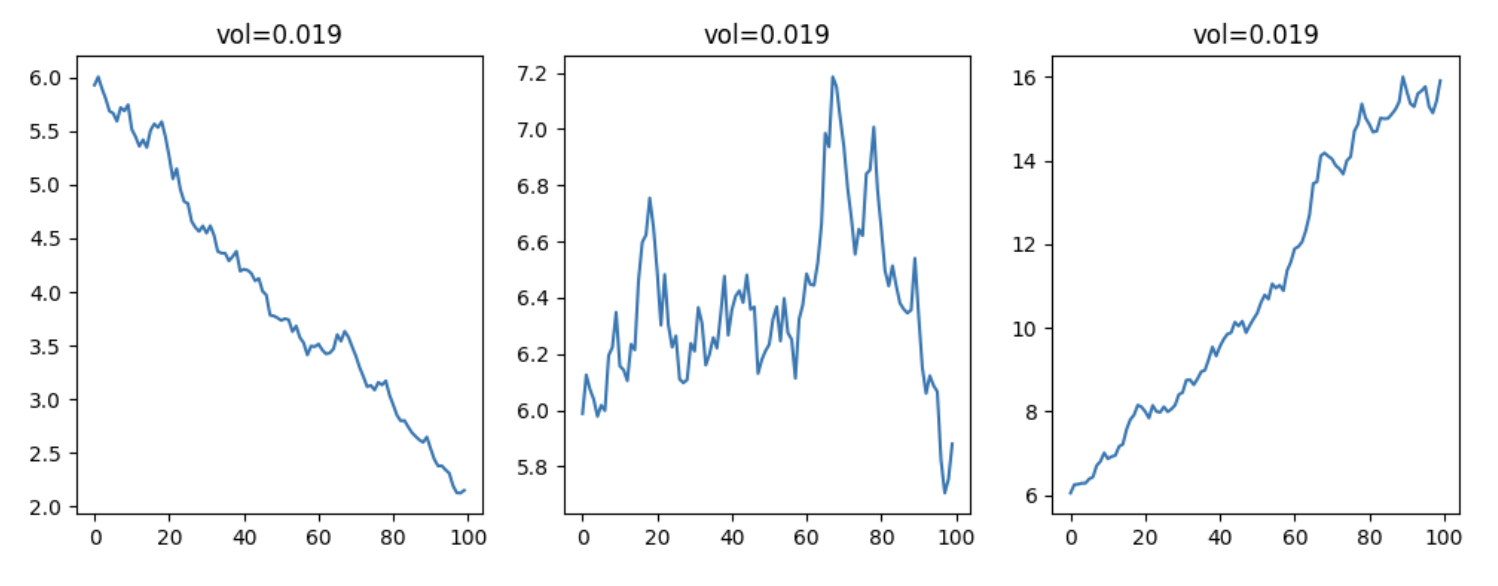
在低波动率条件下，判断股价走势非常容易，我们对价格进行回归，如果得到的直线斜率大于0，则走势是向上的。

这里的关键点是，我们首先要使用月线，至少24个周期以上。在较短的周期上，低波动率的背后没有经济学上的意义支撑。主要代码如下：

for symbol, name, _ in get_secs():bars = get_bars(symbol, 24, ...)if len(bars) < 24:continueclose = bars["close"][-24:]returns = close[1:]/close[:-1] - 1# 计算波动率vol = np.std(returns)# 计算斜率a, b = np.polyfit(np.arange(24), close/close[0], degree=1)result.append((name, symbol, vol, a))df = pd.DataFrame(result, columns=["name", "symbol", "vol", "slope"])df[df.slope>0].nsmallest(10, "vol")

这样我们就选出了趋势向上，波动率最小的10支。当slope接近0时，实际上还不能认为趋势向上，所以，我们可以通过分位数来进行筛选：

quant_25 = df[df.slope>0].slope.quantile(0.25)df[df.slope > quant_25].nsmallest(10, "vol")

结束语

人迹罕至的道路，有时提供更好的旅程。新国九条之后，红利股在投资中的重要性将大大加强，而低波动因子在发现红利股、白马股方面有优秀的选择能力。如果一个市场里的财务数据不那么可靠，那么我们就应该使用低波动因子来代替价值因子。量价数据永远不说谎。如果一家过去看起来很好的公司，最近出了问题，看财报的人永远是最后一个知道的。但股价会提前反映。

这篇关于新国九条下，低波动因子重要性提升！的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---