本文主要是介绍渐进时间复杂度O(n),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
基本操作数
算法的运行速度受计算机性能的影响,所以通常考虑算法效率的不是算法运行的实际用时,而是算法运行所需要进行的基本操作的数量。
像加减乘除、访问变量、给变量赋值等都可以看作基本操作。对基本操作的计数或是估测可以作为评判算法用时的指标。
时间复杂度
在算法竞赛中,我们衡量一个算法的效率时,最重要的不是看它在某个数据规模下的用时,而是看它的用时随数据规模而增长的趋势,即 时间复杂度。
时间复杂度是指算法运行时间与问题规模之间的关系,通常用大 O 表示法来表示。
常见的时间复杂度有O(1), O(logn), O(n), O(nlogn), O(n^2 ), O(2^n)等,其中 O(1) 表示算法的运行时间不随问题规模变化而改变,而O(2^n ) 则表示算法的运行时间随问题规模n呈指数级增长。
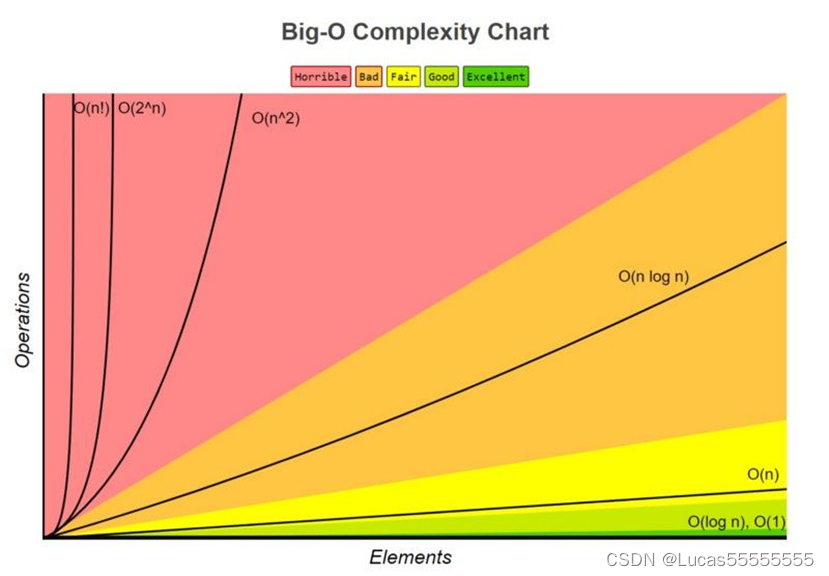
变化趋势意味着我们不用纠结于具体的操作次数和n之间的精确对应关系,也就是不用看具体的函数的参数是什么,而只用看随着数据范围的增大,操作次数的变化是属于哪一类函数。
例如:是常数,还是线性的,还是对数的,还是nlogn的,还是n^2的,还是2^n的,还是阶乘n!的。原因是当n变得非常大的时候,这些不同类型的函数之间的差异值才是明显的,而同一种类型之间的参数不同带来的差异就显得微不足道了,可以忽略不计。这也是为什么O(1)和O(3) 都被称作 O(1)。
例子
for (int i = 1; i <= n; i++)
{j = i;j++;
} 这段代码的时间复杂度O(n)的。分析代码的执行次数,第1行中i=1执行1次, i<=n和i++分别执行n次,第2行、第3行分别执行n次,所以这段代码总共执行4n+1次。从这个结果可以看出,这个算法的耗时是随着n的变化而变化。如果n无限大的时候,1+4n 中的常量1就没有意义了,倍数4的意义也不大。因此时间复杂度直接简化为O(n)。
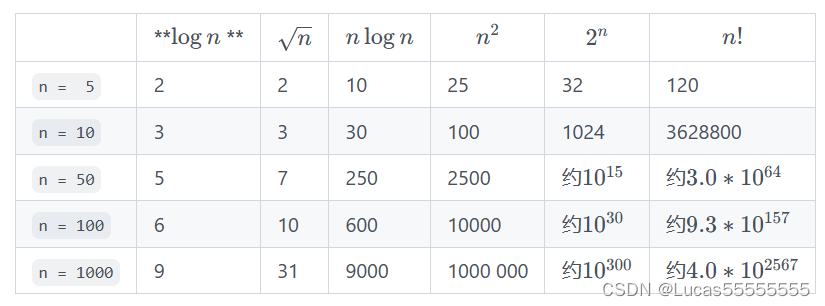
计算次数
O(n)、O(logn)、O(n)、O(nlogn)随着n的增加,复杂度提升不大,因此这些复杂度属于效率高的算法,反观O(2^n)和O(n!)当n增加到50时,复杂度就突破十位数了,这种效率极差的复杂度最好不要出现在程序中。(tips:通常计算机每秒可以计算的次数大约是10的8次方)
最坏、最好、平均
在进行时间复杂度分析时,需要考虑算法的最好、最坏、平均情况时间复杂度。
最好情况时间复杂度是指算法在最优输入情况下的运行时间复杂度,即在所有可能的输入情况中,算法所需的最少时间。例如,对于二分查找算法来说,在目标元素为中间元素的情况下,查找时间为 O(1)。
最坏情况时间复杂度是指算法在最劣输入情况下的运行时间复杂度,即在所有可能的输入情况中,算法所需的最长时间。例如,对于冒泡排序算法来说,最坏情况是需要 O(n^2) 的时间复杂度。
平均情况时间复杂度是指算法在所有可能输入情况下的平均运行时间复杂度。对于某些算法来说,平均情况时间复杂度更能反映算法的运行效率,例如快速排序算法的平均情况时间复杂度为 O(nlogn),而最坏时间复杂度是 O(n^2)。
我们通常所说的时间复杂度大 O是指算法的最坏时间复杂度。这是因为最坏时间复杂度能够给出算法的最长运行时间,可以帮助我们评估算法的性能并预估程序的执行时间。此外,最坏时间复杂度也是一种更保守的衡量指标,即使算法在最坏情况下表现较好,也能够保证算法的性能不会低于最坏时间复杂度。
常见的时间复杂度
常数阶O(1)
代码执行次数是一个常数,不随n的变化而变化,那这个代码的时间复杂度就都是O(1),如下的代码中虽然含有for循环,但循环次数是100次,不随问题规模变化而变化,因此是常数级O(1)的时间复杂度:
for(int i = 1; i <= 100; i++)
{cnt += i;
}线性阶O(n)
这段代码,for循环里面的代码会执行n遍,因此它消耗的时间是随着n的变化而变化的,因此这类代码都可以用O(n)来表示它的时间复杂度。
for(int i = 1; i <= n; i++)
{cnt += i;
}对数阶O(logn)
同样是for循环,但这段代码的时间复杂度是O(logn),因此不能单纯认为for循环就一定是O(n)的。
for(int i = 1; i <= n; i *= 2)
{cnt++;
} 线性对数阶O(nlogn)
线性对数阶O(nlogn) 其实非常容易理解,将时间复杂度为O(logn) 的代码循环n遍的话,那么它的时间复杂度就是 n×O(logn)。
就拿上面的代码加一点修改来举例:
for(int i = 1; i <= n; i++)
{ for(int j = 1; j <= n; j *= 2){cnt++;}
}
平方阶O(n^2 )
平方阶O(n^2)就更容易理解了,如果把O(n)的代码再嵌套循环一遍,它的时间复杂度就是 O(n^2) 了。
for(int i = 1; i <= n; i++)
{for(int j = 1; j <= n; j++){cnt++; }
}阶乘阶O(n!)

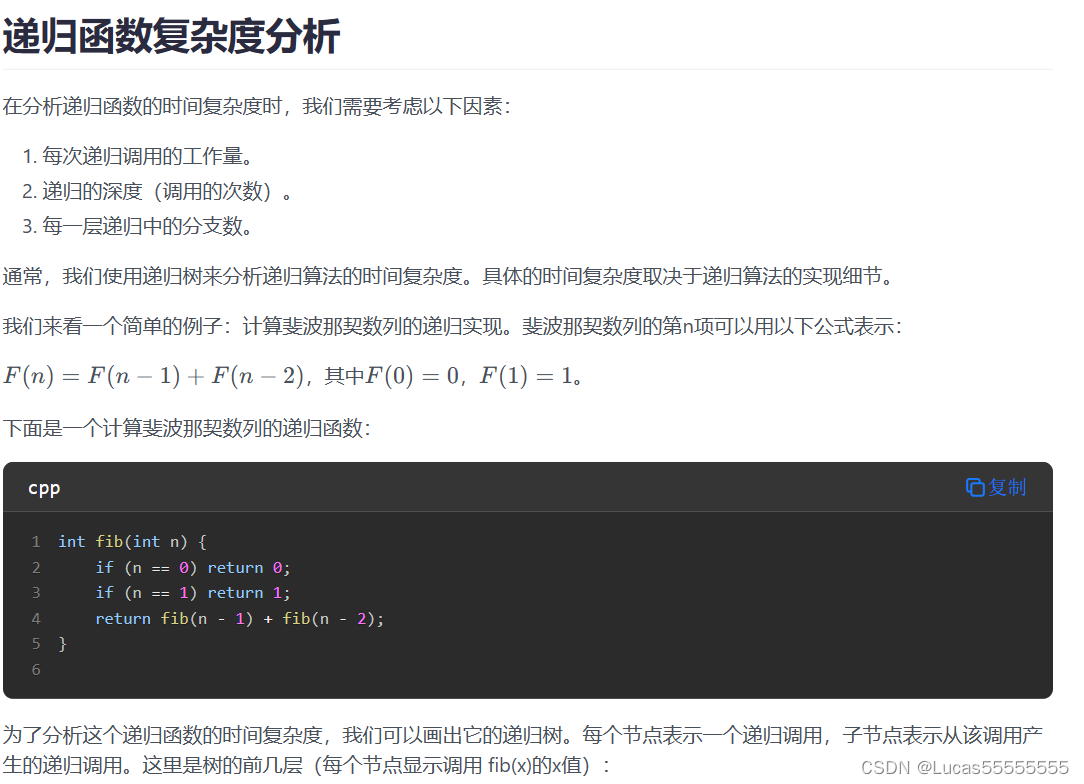
指数阶O(2^n)
void f(int n)
{if(n==1){return 1;}else{return f(n-1)+f(n-2);}
}
彩蛋
#include <bits/stdc++.h>
using namespace std;
int main()
{cout<<"O(1):"<<endl;cout<<"int n=100;"<<endl;cout<<"int a=n;"<<endl;cout<<endl;cout<<"O(logn):"<<endl;cout<<"while(i<=n)"<<endl;cout<<"{"<<endl;cout<<" i*=2;"<<endl;cout<<"}"<<endl;cout<<endl;cout<<"O(n):"<<endl;cout<<"for(int i=1;i<=n;i++)"<<endl;cout<<"{"<<endl;cout<<" cout<<1;"<<endl;cout<<"}"<<endl;cout<<endl;cout<<"O(nlogn)(logn重复n遍):"<<endl;cout<<"for(int i = 1; i <= n; i++)"<<endl;cout<<"{"<<endl; cout<<" for(int j = 1; j <= n; j *= 2)"<<endl;cout<<" {"<<endl;cout<<" cnt++;"<<endl;cout<<" }"<<endl;cout<<"}"<<endl;cout<<endl;cout<<"O(n*n):"<<endl;cout<<"for(int i=1;i<=n;i++)"<<endl;cout<<"{"<<endl;cout<<" for(int j=1;j<=n;j++)"<<endl;cout<<" {"<<endl;cout<<" cout<<1;"<<endl;cout<<" }"<<endl;cout<<"}"<<endl;cout<<endl;cout<<"O(2^n):"<<endl;cout<<"void f(int n)"<<endl;cout<<"{"<<endl;cout<<" if(n==1)"<<endl;cout<<" {"<<endl;cout<<" return 1;"<<endl;cout<<" }"<<endl;cout<<" else"<<endl;cout<<" {"<<endl;cout<<" return f(n-1)+f(n-2);"<<endl;cout<<" }"<<endl;cout<<"}"<<endl;return 0;
}learn more!!!
Big-O Algorithm Complexity Cheat Sheet (Know Thy Complexities!) @ericdrowell
这篇关于渐进时间复杂度O(n)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




