层次分析法（AHP）详细注释的MATLAB代码（可读性强）

本文主要是介绍层次分析法（AHP）详细注释的MATLAB代码（可读性强），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

目录

一、层次分析法简述

二、层次分析法相关重点

三、层次分析法的MATLAB代码（包含详细注释）

3.1 算术平均法计算权重的函数代码

3.2 几何平均法计算权重的函数代码

3.3 特征值法计算权重的函数代码

3.4 层次分析法主程序的代码

三、相关文件的下载

四、总结

---

一、层次分析法简述

        层次分析法（Analytic Hierarchy Process，AHP）是一种多准则决策方法，其核心思想是将一个复杂的决策问题分解成多个层次，然后通过比较不同因素之间的相对重要性来做出决策。主要目的是给评价指标赋相应的权重。

第一步：构建层次结构： 首先，将要解决的问题分解成一个层次结构，包括目标层、准则层或指标层、方案层等层次。这些层次之间是逐层递进的关系，最顶层是最终的决策目标，中间层一般是我们的评价指标，底层是具体的方案或选项。

第二步：两两比较： 对每个层次中的元素进行两两比较，以确定它们之间的相对重要性。比较的结果以矩阵形式表示，称为判断矩阵。决策者使用尺度从1到9的标准判断两个元素之间的重要性，1表示相同重要性，9表示极端重要性差异，中间值表示相对程度。

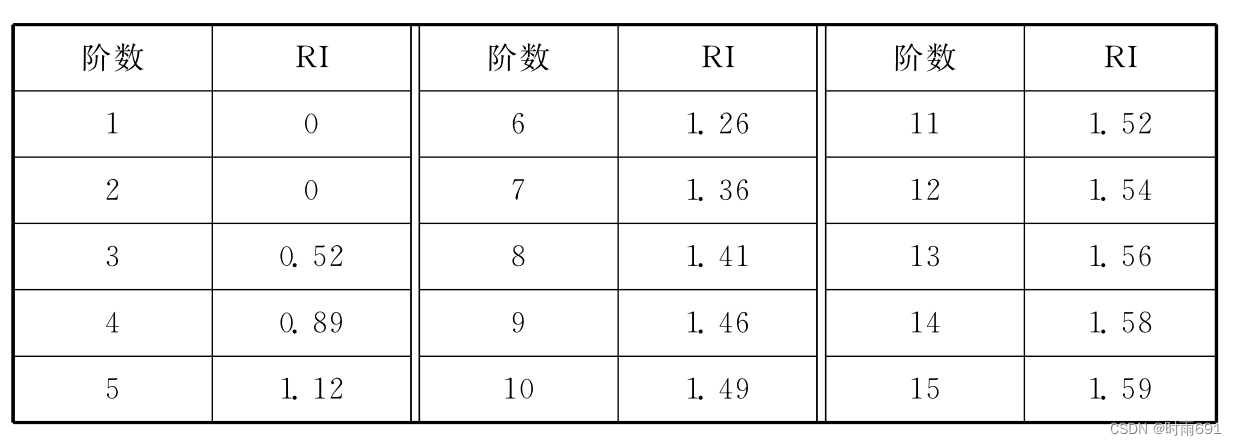
第三步：一致性检验： 对比每个判断矩阵的一致性指标CI和随机平均一致性指标RI，以确定决策者的比较是否一致。如果一致性较差，可能需要重新修改判断矩阵，直到达到一定的一致性标准。

第四步：计算权重向量： 根据判断矩阵，计算出每个层次中各元素的权重。主要通过算术平均法、几何平均法、特征值法求解权重向量。

第五步：综合评估： 将各层次的权重以及方案的评价指标综合起来，计算出各个方案的综合得分。这样可以帮助决策者找到最佳的方案或决策。

        在很多综合评价类的问题中，我们往往需要知道那些指标是比较重要的，那些指标是不太重要的，例如我们在考研的过程中需要经过初试和面试，有的学校将初试成绩取60%，复试成绩取40%，此时的权重向量为U=[0.6，0.4]，根据这个权重，从而决定这个学生是否录取。为了描述这种指标的重要程度，我们需要引入一个重要的概念——权重，权重是一个相对于整体评价而言的量化概念，用于衡量某个因素在整体评价中的相对重要性。

        在实际应用中，一般情况下是使用主观经验法来确定权重，但这个方法有一个缺点就是主观性太强，评价并不是很科学，所有有没有一种方法可以求出评价指标的权重？求权重的方法有很多种，例如：TOPSIS法、熵权法、层次分析法等。TOPSIS法与熵权法是基于已有数据来进行评价，相较于层次分析法比较客观，如果数据不是很明确，且数据对指标与指标之间的影响很小，建议使用层次分析法。

二、层次分析法相关重点

相关内容的讲解可以参考以下两个视频（个人觉得把这两位老师的讲解看完，已经可以完全掌握层次分析法）：

数学建模层次分析法模型（综合评价类问题）_哔哩哔哩_bilibili

地址：https://www.bilibili.com/video/BV1GJ411k7cj/?spm_id_from=333.337.search-card.all.click&vd_source=61fc0d2ec19e61330ac909c734d9d6cb

层次分析法模型讲解(附matlab和python代码) 【数学建模快速入门】数模加油站 江北_哔哩哔哩_bilibili

地址：

https://www.bilibili.com/video/BV1Yh411u7q6/?spm_id_from=333.337.search-card.all.click&vd_source=61fc0d2ec19e61330ac909c734d9d6cb

三、层次分析法的MATLAB代码（包含详细注释）

3.1 算术平均法计算权重的函数代码

%% 算术平均法计算权重
function [weight] = arithmetic_mean(inputA)
% 将判断矩阵每列求和
asum = sum(inputA);
% 获取的矩阵A的列数和行数
[~,m] = size(inputA);% 此时默认矩阵为方阵
% 将asum变成方阵，方便后面对应相处，从而归一化
asumrepmat = repmat(asum,m,1);
% 件矩阵A归一化可得矩阵B
B = inputA./asumrepmat;
% 将矩阵B按行求和，每个元素除以矩阵的行数
weight = sum(B,2)/m;
% eight便是权重
end

3.2 几何平均法计算权重的函数代码

%% 几何平均法计算权重
function [weight] = geometric_mean(inputA)
% 将判断矩阵的元素按照行相乘得到一个新的列向量
B = prod(inputA,2);
% 获取矩阵input的行数和列数
[~,n] = size(inputA);
% 将新的向量的每个分量开n次方
B = B.^(1/n);
% 对向量B进行归一化
weight = B./sum(B);
end

3.3 特征值法计算权重的函数代码

%% 特征值法计算权重
function [weight] = characteristics(inputA)
% 求出矩阵inputA的最大特征值及对应的特征向量
[v,d] = eig(inputA);% v是特征向量，d是特征值对角矩阵
max_d = max(max(d));
% 找出最大特征值对应的特征向量
[~,c] = find(d == max_d,1); % find查找，查找满足d==max_d条件的一个元素，r是行，c是列
% 将找到的特征向量归一化
weight =abs(v(:,c))./abs(sum(v(:,c)));
end

3.4 层次分析法主程序的代码

%% 层次分析法一致性检验的代码
clear
clc
% 提供的测试数据，第一个不通过一致性检验，第二个通过一致性检验
% A = [1 2 3 5;1/2 1 1/2 2;1/3 2 1 1/2;1/5 1/2 2 1]
% A = [1 2 3 5;1/2 1 1/2 2;1/3 2 1 2;1/5 1/2 1/2 1]
A = input("请输入判断矩阵A：");
[n,m] = size(A); % 获取矩阵A的行和列，n是行，m是列
% 检查输入的是否是方阵
if ismatrix(A) && n==m% 判断是否是正互反矩阵for i = 1:nfor j = 1:mif A(i,j)*A(j,i) ~= 1error("输入错误，判断矩阵不是正互反矩阵！")endendenddisp("输入类型正确！")
elseerror("出错！输入结果不是方阵！")
end
% 求出矩阵A的最大特征值及对应的特征向量
[V,D] = eig(A); %求矩阵的特征值和特征向量，V为特征值，D为特征向量
% 注：此时D是一个对角线为特征值，其它元素为0的矩阵
max_D = max(max(D)); %求出矩阵A的最大的特征值
% 计算一致性指标CI
CI = (max_D-n) / (n-1);%计算一致性指标的计算公式
% 平均随机一致性指标RI(共15个)
RI = [0 0 0.52 0.89 1.12 1.26 1.26 1.36 1.41 1.49 1.52 1.54 1.56 1.58 1.59];
% 
CR = CI/RI(n);
format long
disp("一致性指标CI为");
disp(CI)
disp("对应的平均随机一致性指标RI为")
disp(RI(n))
disp("一致性比例CR为")
disp(CR)
if CR == 0disp("该矩阵为一致矩阵，一致性检验通过！")
elseif CR < 0.10disp("由于CR<0.1，因此该矩阵通过一致性检验！")
elsedisp("由于CR>=0.1，因此该矩阵不通过一致性检验，需要修改判断矩阵！")return
end
while truedisp("请选择方法")disp("输入0，终止执行程序！")disp("输入1，利用算术平均法计算权重")disp("输入2，利用几何平均法计算权重")disp("输入3，利用特征值法计算权重")disp("输入其它数字，则重新输入判断矩阵！")key = input("请输入：");if key == 0disp("程序结束，感谢使用！")breakelseif key == 1disp("你选择的是利用算术平均法计算权重")pause(1)weight_need = arithmetic_mean(A);disp("算术平均法计算权重的结果为：")disp(weight_need)elseif key == 2disp("你选择的是利用几何平均法计算权重")pause(1)weight_need = geometric_mean(A);disp("几何平均法计算权重的结果为：")disp(weight_need) elseif key == 3disp("你选择的是利用特征值法计算权重")pause(1)weight_need = characteristics(A);disp("特征值法计算权重的结果为：")disp(weight_need) elsereturn % 结束程序运行！end
end

三、相关文件的下载

层次分析法（AHP）主程序运行文件资源-CSDN文库

层次分析法（AHP）算术平均法求权重的函数文件资源-CSDN文库

层次分析法（AHP）几何平均法求权重的函数文件资源-CSDN文库

层次分析法（AHP）特征值法求权重的函数文件资源-CSDN文库

四、总结

        本文主要介绍层次分析法的MATLB的代码，代码已经做了详细的注释了，方便各位读者理解。本文并没有详细的介绍层次分析法，后面我将会根据时间更新一篇详细的教程，大家可以关注期待一下，如果你认为本文对你学习层次分析法有帮助可以点赞收藏一下，感谢您的支持！

这篇关于层次分析法（AHP）详细注释的MATLAB代码（可读性强）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---