自然启发的搜索算法

2024-04-21 18:32
文章标签 自然 搜索算法 启发

本文主要是介绍自然启发的搜索算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

旅行商问题（TSP）:一个销售员要要访问n座城市，从某座城市出发，在任意两座城市可以计算距离的前提下，希望以最短路径把每座城市都访问一遍并最终回到出发的城市。

TSP通常引入模拟退火算法、遗传算法、蚁群算法来解决。 

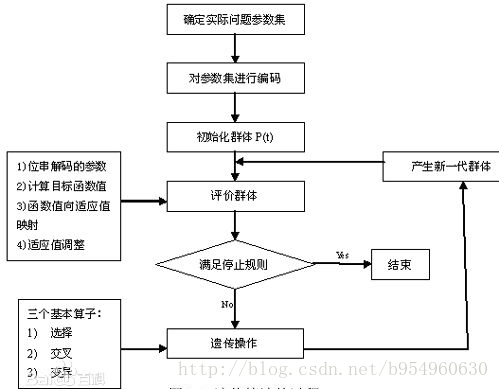
模拟退火算法

实现流程：

模æéç«ç®æ³çåçãä¼ç¼ºç¹ãæµç¨ãåºç¨å®ä¾

实现代码：

/** 使用模拟退火算法(SA)求解TSP问题(以中国TSP问题为例)* 参考自《Matlab 智能算法30个案例分析》* 模拟退火的原理这里略去，可以参考上书或者相关论文* update: 16/12/11* author:lyrichu* email:919987476@qq.com*/
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<time.h>
#include<math.h>
#define T0 50000.0  // 初始温度
#define T_end (1e-8)
#define q  0.98   // 退火系数
#define L 1000  // 每个温度时的迭代次数，即链长
#define N 31  // 城市数量
int city_list[N]; // 用于存放一个解
double city_pos[N][2] = {{1304,2312},{3639,1315},{4177,2244},{3712,1399},{3488,1535},{3326,1556},{3238,1229},{4196,1004},{4312,790},{4386,570},{3007,1970},{2562,1756},{2788,1491},{2381,1676},{1332,695},{3715,1678},{3918,2179},{4061,2370},{3780,2212},{3676,2578},{4029,2838},{4263,2931},{3429,1908},{3507,2367},{3394,2643},{3439,3201},{2935,3240},{3140,3550},{2545,2357},{2778,2826},{2370,2975}}; // 中国31个城市坐标
//函数声明
double distance(double *,double *); // 计算两个城市距离
double path_len(int *);  // 计算路径长度
void  init();  //初始化函数
void create_new(); // 产生新解
// 距离函数
double distance(double * city1,double * city2)
{double x1 = *city1;double y1 = *(city1+1);double x2 = *(city2);double y2 = *(city2+1);double dis = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));return dis;
}// 计算路径长度
double path_len(int * arr)
{double path = 0; // 初始化路径长度int index = *arr; // 定位到第一个数字(城市序号)for(int i=0;i<N-1;i++){int index1 = *(arr+i);int index2 = *(arr+i+1);double dis = distance(city_pos[index1-1],city_pos[index2-1]);path += dis;}int last_index = *(arr+N-1); // 最后一个城市序号int first_index = *arr; // 第一个城市序号double last_dis = distance(city_pos[last_index-1],city_pos[first_index-1]);path = path + last_dis;return path; // 返回总的路径长度
}// 初始化函数
void init()
{for(int i=0;i<N;i++)city_list[i] = i+1;  // 初始化一个解
}// 产生一个新解
// 此处采用随机交叉两个位置的方式产生新的解
void create_new()
{double r1 = ((double)rand())/(RAND_MAX+1.0);double r2 = ((double)rand())/(RAND_MAX+1.0);int pos1 = (int)(N*r1); //第一个交叉点的位置int pos2 = (int)(N*r2);int temp = city_list[pos1];city_list[pos1] = city_list[pos2];city_list[pos2] = temp;   // 交换两个点
}// 主函数
int main(void)
{srand((unsigned)time(NULL)); //初始化随机数种子time_t start,finish;start = clock(); // 程序运行开始计时double T;int count = 0; // 记录降温次数T = T0; //初始温度init(); //初始化一个解int city_list_copy[N]; // 用于保存原始解double f1,f2,df; //f1为初始解目标函数值，f2为新解目标函数值，df为二者差值double r; // 0-1之间的随机数，用来决定是否接受新解while(T > T_end) // 当温度低于结束温度时，退火结束{for(int i=0;i<L;i++){memcpy(city_list_copy,city_list,N*sizeof(int)); // 复制数组create_new(); // 产生新解f1 = path_len(city_list_copy);f2 = path_len(city_list);df = f2 - f1;// 以下是Metropolis准则if(df >= 0){r = ((double)rand())/(RAND_MAX);if(exp(-df/T) <= r) // 保留原来的解{memcpy(city_list,city_list_copy,N*sizeof(int));}}}T *= q; // 降温count++;}finish = clock(); // 退火过程结束double duration = ((double)(finish-start))/CLOCKS_PER_SEC; // 计算时间printf("采用模拟退火算法，初始温度T0=%.2f,降温系数q=%.2f,每个温度迭代%d次,共降温%d次，得到的TSP最优路径为:\n",T0,q,L,count);for(int i=0;i<N-1;i++)  // 输出最优路径{printf("%d--->",city_list[i]);}printf("%d\n",city_list[N-1]);double len = path_len(city_list); // 最优路径长度printf("最优路径长度为:%lf\n",len);printf("程序运行耗时:%lf秒.\n",duration);return 0;
}

 

遗传算法

实现流程：

è¿éåå¾çæè¿°

/**遗传算法(GA) 解决TSP 问题*案例参考自《MATLAB 智能算法30个案例分析》*本例以14个城市为例，14个城市的位置坐标如下(括号内第一个元素为X坐标，第二个为纵坐标)：1:(16.47,96.10)  2:(16.47,94.44)  3:(20.09,92.54)*4:(22.39,93.37) 5:(25.23,97.24)  6:(22.00,96.05) 7:(20.47,97.02)  8:(17.20,96.29) 9:(16.30,97.38) 10:(14.05,98.12) 11:(16.53,97.38)*12:(21.52,95.59)  13:(19.41,97.13)  14:(20.09,92.55)*遗传算法实现的步骤为:(1)编码 (2) 种群初始化 (3) 构造适应度函数 (4) 选择操作 (5) 交叉操作 (6) 变异操作 (7) 进化逆转操作* 具体实现的步骤这里不详细说，参考《MATLAB 智能算法30个案例分析》P38 - P40* update in 16/12/4* author:Lyrichu* email:919987476@qq.com*/
#include<stdio.h>
#include<stdlib.h>
#include<math.h>
#include<time.h>
#define maxgen 200  // 最大进化代数
#define sizepop 100 // 种群数目
#define pcross 0.6 // 交叉概率
#define pmutation 0.1 // 变异概率
#define lenchrom 14 // 染色体长度(这里即为城市个数)
double city_pos[lenchrom][2] = {{16.47,96.10},{16.47,94.44},{20.09,92.54},{22.39,93.37},{25.23,97.24},{22.00,96.05},{20.47,97.02},{17.20,96.29},{16.30,97.38},{14.05,98.12},{16.53,97.38},{21.52,95.59},{19.41,97.13},{20.09,92.55}}; // 定义二维数组存放14个城市的X、Y坐标
int chrom[sizepop][lenchrom]; // 种群
int best_result[lenchrom]; // 最佳路线
double min_distance; // 最短路径长度// 函数声明
void init(void); // 种群初始化函数
double distance(double *,double *); // 计算两个城市之间的距离
double * min(double *); // 计算距离数组的最小值
double path_len(int *); // 计算某一个方案的路径长度，适应度函数为路线长度的倒数
void Choice(int [sizepop][lenchrom]); // 选择操作
void Cross(int [sizepop][lenchrom]); // 交叉操作
void Mutation(int [sizepop][lenchrom]); // 变异操作
void Reverse(int [sizepop][lenchrom]); // 逆转操作// 种群初始化
void init(void)
{int num = 0;while(num < sizepop){for(int i=0;i<sizepop;i++)for(int j=0;j<lenchrom;j++)chrom[i][j] = j+1;num++;for(int i=0;i<lenchrom-1;i++){for(int j=i+1;j<lenchrom;j++){int temp = chrom[num][i];chrom[num][i] = chrom[num][j];chrom[num][j] = temp; // 交换第num个个体的第i个元素和第j个元素num++;if(num >= sizepop)break;}if(num >= sizepop)break;}// 如果经过上面的循环还是无法产生足够的初始个体，则随机再补充一部分// 具体方式就是选择两个基因位置，然后交换while(num < sizepop){double r1 = ((double)rand())/(RAND_MAX+1.0);double r2 = ((double)rand())/(RAND_MAX+1.0);int p1 = (int)(lenchrom*r1); // 位置1int p2 = (int)(lenchrom*r2); // 位置2int temp = chrom[num][p1];chrom[num][p1] = chrom[num][p2];chrom[num][p2] = temp;    // 交换基因位置num++;}}
}// 距离函数
double distance(double * city1,double * city2)
{double x1 = *city1;double y1 = *(city1+1);double x2 = *(city2);double y2 = *(city2+1);double dis = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));return dis;
}
// min()函数
double * min(double * arr)
{static double best_index[2];double min_dis = *arr;double min_index = 0;for(int i=1;i<sizepop;i++){double dis = *(arr+i);if(dis < min_dis){min_dis = dis;min_index = i;}}best_index[0] = min_index;best_index[1] = min_dis;return best_index;
}// 计算路径长度
double path_len(int * arr)
{double path = 0; // 初始化路径长度int index = *arr; // 定位到第一个数字(城市序号)for(int i=0;i<lenchrom-1;i++){int index1 = *(arr+i);int index2 = *(arr+i+1);double dis = distance(city_pos[index1-1],city_pos[index2-1]);path += dis;}int last_index = *(arr+lenchrom-1); // 最后一个城市序号int first_index = *arr; // 第一个城市序号double last_dis = distance(city_pos[last_index-1],city_pos[first_index-1]);path = path + last_dis;return path; // 返回总的路径长度
}// 选择操作
void Choice(int chrom[sizepop][lenchrom])
{double pick;double choice_arr[sizepop][lenchrom];double fit_pro[sizepop];double sum = 0;double fit[sizepop]; // 适应度函数数组(距离的倒数)for(int j=0;j<sizepop;j++){double path = path_len(chrom[j]);double fitness = 1/path;fit[j] = fitness;sum += fitness;}for(int j=0;j<sizepop;j++){fit_pro[j] = fit[j]/sum; // 概率数组}// 开始轮盘赌for(int i=0;i<sizepop;i++){pick = ((double)rand())/RAND_MAX; // 0到1之间的随机数  for(int j=0;j<sizepop;j++){pick = pick - fit_pro[j];if(pick<=0){for(int k=0;k<lenchrom;k++)choice_arr[i][k] = chrom[j][k]; // 选中一个个体break;    }}}for(int i=0;i<sizepop;i++){for(int j=0;j<lenchrom;j++)chrom[i][j] = choice_arr[i][j];}
}//交叉操作
void Cross(int chrom[sizepop][lenchrom])
{double pick;double pick1,pick2;int choice1,choice2;int pos1,pos2;int temp;int conflict1[lenchrom]; // 冲突位置int conflict2[lenchrom];int num1,num2;int index1,index2;int move = 0; // 当前移动的位置while(move<lenchrom-1){pick = ((double)rand())/RAND_MAX; // 用于决定是否进行交叉操作if(pick > pcross){move += 2;continue; // 本次不进行交叉}// 采用部分映射杂交choice1 = move; // 用于选取杂交的两个父代choice2 = move+1; // 注意避免下标越界pick1 = ((double)rand())/(RAND_MAX+1.0);pick2 = ((double)rand())/(RAND_MAX+1.0);pos1 = (int)(pick1*lenchrom); // 用于确定两个杂交点的位置pos2 = (int)(pick2*lenchrom); while(pos1 > lenchrom -2 || pos1 < 1){pick1 = ((double)rand())/(RAND_MAX+1.0);pos1 = (int)(pick1*lenchrom);}while(pos2 > lenchrom -2 || pos2 < 1){pick2 = ((double)rand())/(RAND_MAX+1.0);pos2 = (int)(pick2*lenchrom);}if(pos1 > pos2){temp = pos1;pos1 = pos2;pos2 = temp; // 交换pos1和pos2的位置}for(int j=pos1;j<=pos2;j++){temp = chrom[choice1][j];chrom[choice1][j] = chrom[choice2][j];chrom[choice2][j] = temp; // 逐个交换顺序}num1 = 0;num2 = 0;if(pos1 > 0 && pos2 < lenchrom-1){for(int j =0;j<=pos1-1;j++){for(int k=pos1;k<=pos2;k++){if(chrom[choice1][j] == chrom[choice1][k]){conflict1[num1] = j;num1++;}if(chrom[choice2][j] == chrom[choice2][k]){conflict2[num2] = j;num2++;}}}for(int j=pos2+1;j<lenchrom;j++){for(int k=pos1;k<=pos2;k++){if(chrom[choice1][j] == chrom[choice1][k]){conflict1[num1] = j;num1++;}if(chrom[choice2][j] == chrom[choice2][k]){conflict2[num2] = j;num2++;                     }                 }}}if((num1 == num2) && num1 > 0){for(int j=0;j<num1;j++){index1 = conflict1[j];index2 = conflict2[j];temp = chrom[choice1][index1]; // 交换冲突的位置chrom[choice1][index1] = chrom[choice2][index2];chrom[choice2][index2] = temp;}}move += 2;}
}// 变异操作
// 变异策略采取随机选取两个点，将其对换位置
void Mutation(int chrom[sizepop][lenchrom])
{double pick,pick1,pick2;int pos1,pos2,temp;for(int i=0;i<sizepop;i++){pick = ((double)rand())/RAND_MAX; // 用于判断是否进行变异操作if(pick > pmutation)continue;pick1 = ((double)rand())/(RAND_MAX+1.0);pick2 = ((double)rand())/(RAND_MAX+1.0);pos1 = (int)(pick1*lenchrom); // 选取进行变异的位置pos2 = (int)(pick2*lenchrom);while(pos1 > lenchrom-1){pick1 = ((double)rand())/(RAND_MAX+1.0);pos1 = (int)(pick1*lenchrom);}while(pos2 > lenchrom-1){pick2 = ((double)rand())/(RAND_MAX+1.0);pos2 = (int)(pick2*lenchrom);}temp = chrom[i][pos1];chrom[i][pos1] = chrom[i][pos2];chrom[i][pos2] = temp;}
}// 进化逆转操作
void Reverse(int chrom[sizepop][lenchrom])
{double pick1,pick2;double dis,reverse_dis;int n;int flag,pos1,pos2,temp;int reverse_arr[lenchrom];for(int i=0;i<sizepop;i++){flag = 0; // 用于控制本次逆转是否有效while(flag == 0){pick1 = ((double)rand())/(RAND_MAX+1.0);pick2 = ((double)rand())/(RAND_MAX+1.0);pos1 = (int)(pick1*lenchrom); // 选取进行逆转操作的位置pos2 = (int)(pick2*lenchrom);while(pos1 > lenchrom-1){pick1 = ((double)rand())/(RAND_MAX+1.0);pos1 = (int)(pick1*lenchrom);}while(pos2 > lenchrom -1){pick2 = ((double)rand())/(RAND_MAX+1.0);pos2 = (int)(pick2*lenchrom);}if(pos1 > pos2){temp = pos1;pos1 = pos2;pos2 = temp; // 交换使得pos1 <= pos2}if(pos1 < pos2){for(int j=0;j<lenchrom;j++)reverse_arr[j] = chrom[i][j]; // 复制数组n = 0; // 逆转数目for(int j=pos1;j<=pos2;j++){reverse_arr[j] = chrom[i][pos2-n]; // 逆转数组n++; }reverse_dis = path_len(reverse_arr); // 逆转之后的距离dis = path_len(chrom[i]); // 原始距离if(reverse_dis < dis){for(int j=0;j<lenchrom;j++)chrom[i][j] = reverse_arr[j]; // 更新个体}}flag = 1;}    }   
}// 主函数
int main(void)
{time_t start,finish;start = clock(); // 开始计时srand((unsigned)time(NULL)); // 初始化随机数种子init(); // 初始化种群int best_fit_index = 0; //最短路径出现代数double distance_arr[sizepop];double dis;for(int j=0;j<sizepop;j++){dis = path_len(chrom[j]);distance_arr[j] = dis;}double * best_index = min(distance_arr); // 计算最短路径及序号min_distance = *(best_index+1); // 最短路径int index = (int)(*best_index); // 最短路径序号for(int j=0;j<lenchrom;j++)best_result[j] = chrom[index][j]; // 最短路径序列// 开始进化double * new_arr;double new_min_dis;int new_index;for(int i=0;i<maxgen;i++) {Choice(chrom); // 选择Cross(chrom); //交叉Mutation(chrom); //变异Reverse(chrom); // 逆转操作for(int j=0;j<sizepop;j++)distance_arr[j] = path_len(chrom[j]); // 距离数组new_arr = min(distance_arr);new_min_dis = *(new_arr+1); //新的最短路径if(new_min_dis < min_distance){min_distance = new_min_dis; // 更新最短路径new_index =(int)(*new_arr);for(int j=0;j<lenchrom;j++)best_result[j] = chrom[new_index][j]; // 更新最短路径序列best_fit_index = i+1; // 最短路径代数}}
finish = clock(); // 计算结束
double duration = ((double)(finish-start))/CLOCKS_PER_SEC; // 计算耗时
printf("本程序使用遗传算法求解规模为%d的TSP问题,种群数目为:%d,进化代数为:%d\n",lenchrom,sizepop,maxgen);
printf("得到最短路径为:%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d-->%d\n",best_result[0],best_result[1],best_result[2],best_result[3],best_result[4],best_result[5],best_result[6],best_result[7],best_result[8],best_result[9],best_result[10],best_result[11],best_result[12],best_result[13]);
printf("最短路径长度为:%lf,得到最短路径在第%d代.\n",min_distance,best_fit_index);
printf("程序耗时:%lf秒.\n",duration);
return 0;
}

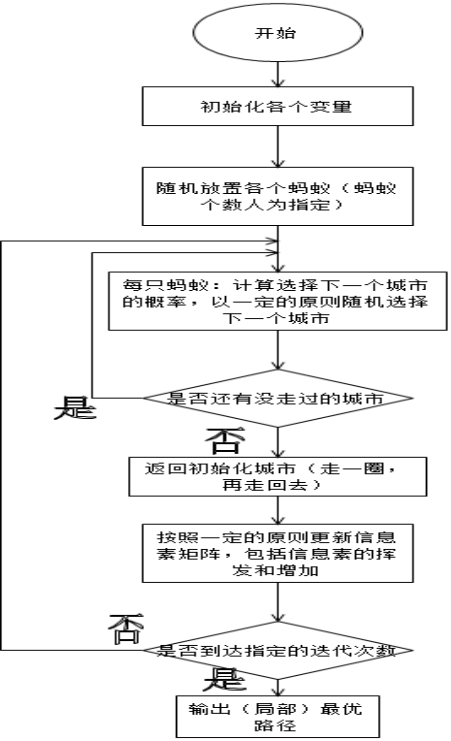
蚁群算法

实现流程：

#include<iostream>
#include<cmath>
using namespace std;
//使用10个蚂蚁，进行10个城市的TSP问题求解。
const int MMax = 9999;//蚂蚁数量,蚂蚁数量根据城市数量决定。
const int NMax = 500;//城市数量最大数量，超过出错
const int m=999;//蚂蚁数量
const int n=5;//城市数量
const double Q = 9 ;//常量
const int K = 1000;//循环总次数
double Phe[NMax][NMax];//边对应的信息素浓度
int LK;//蚂蚁此循环中的总路径长度
int Path[MMax][NMax];//记录蚂蚁的路径，用于防止走重复的路。记录的是点
int ant;//蚂蚁当前所在点
int i,j,k,p;//循环使用
double Dis = 0.1;//每次信息素 消失的速率
int sameNum,samePhe[NMax];//每次去寻找信息素最多的边，如初始情况，信息素量都相同时，要
//随机的去从中选取边。
int bugNum,bugTry[NMax];//出错情况下进行的选择
double bugP = 0.90;//每一次操作的出错概率
//后来发现，出错概率要结合蚂蚁数与城市数进行判断，而定值Q为估计距离
int start=0;//出发点，城市编号从0 - n-1.
double Max;//用来选取最多信息素的边
bool Passed[NMax];//用来判断城市是否已经经过，是否可以选取
const int inf = 9999;
double D[n][n];
//double city_pos[n][2] = {{0,0},{1,0},{2,0},{3,0},{0,1},{1,1},{2,1},{3,1},{0,2},{1,2},{2,2},{3,2},{0,3},{1,3},{2,3},{3,3}}; // 定义二维数组存放16个城市的X、Y坐标
double city_pos[n][2] = {{0,0},{4,1},{3,3},{1,4},{0,2}};//定义二维数组存放n个城市的X、Y坐标
/*int D[9][9]={0,   1, inf,   1, inf, inf, inf, inf, inf,1,   0,   1, inf,   1, inf, inf, inf, inf,inf,   1,   0, inf, inf,   1, inf, inf, inf,1, inf, inf,   0,   1, inf,   1, inf, inf,inf,   1, inf,   1,   0,   1, inf,   1, inf,inf, inf,   1, inf,   1,   0, inf, inf,   1,inf, inf, inf,   1, inf, inf,   0,   1, inf,inf, inf, inf, inf,   1, inf,   1,   0,   1,inf, inf, inf, inf, inf,   1, inf,   1,   0
};*//********************************距离函数********************************/
double distance(double * city1,double * city2)
{double x1 = *city1;double y1 = *(city1+1);double x2 = *(city2);double y2 = *(city2+1);//double dis = sqrt((x1-x2)*(x1-x2)+(y1-y2)*(y1-y2));//欧氏距离double dis = fabs(x1-x2)+fabs(y1-y2);//曼哈顿距离return dis;
}/********************************主函数********************************/
int main()
{//生成距离矩阵for(int i=0;i<n;i++){for(int j=0;j<n;j++){	if(i!=j){double dis = distance(city_pos[i],city_pos[j]);D[i][j]=dis;}elseD[i][j]=1e-4;}}//初始化每条边上的信息素浓度，初始时每条边上的信息素浓度相同for(i = 0;i < n;i++)for(j = 0; j < n;j++) Phe[i][j] = 1;//每只蚂蚁的出发点都固定for(i = 0;i< m;i++)Path[i][0] = start;for(k = 0;k < K;k++){//每次循环后，进行信息素的消逝for(i = 0;i < n;i++)for(j = 0; j < n;j++) Phe[i][j] *= Dis ;srand((unsigned)time(NULL)); for(i = 0;i < m;i++){//对于每只蚂蚁，进行一次循环	ant = start;//蚂蚁当前所在城市//初始化蚂蚁经过路径for(j = 0;j < n;j++)Passed[j] = false;//蚂蚁未经过路径Passed[ant] = true;//蚂蚁出发时经过路径for(j = 1;j < n;j++){//每只蚂蚁选n-1次边Max = 0;sameNum  = 0 ;bugNum = 0;for(p = 0;p < n;p++)if(!Passed[p])Max = Max > Phe[ant][p] ? Max : Phe[ant][p] ;//寻找周围边上信息素的最大值for(p = 0;p < n;p++)if(Max == Phe[ant][p])if(!Passed[p])samePhe[sameNum++] = p;//记录信息素取最大值时，对应的city编号和数量for(p = 0;p < n;p++)if(!Passed[p])bugTry[bugNum++] = p;//记录出错情况下，对应的city编号和数量if( (double)rand() /32765 < bugP)ant = samePhe[ rand() % sameNum ] ;//用随机数，从中选中一条边elseant = bugTry [ rand() % bugNum ] ;//出错情况下，随机选一条边Passed[ant] = true;//路径经过Path[i][j] = ant;//保存路径}}//完成对每一个蚂蚁的操作后，进行增加信息素的操作，使用Ant-Circle System模型for(i = 0; i < m;i++){LK  = 0 ;for(j = 0; j < n-1;j++)LK += D[Path[i][j]][Path[i][j+1]];//计算每一次循环中蚂蚁的总路程LK += D[Path[i][j]][Path[i][0]];//回到初始点for(j = 0; j < n-1;j++)Phe[Path[i][j]][Path[i][j+1]] += Q/LK ;//边对应的信息素浓度之和Phe[Path[i][j]][Path[i][0]] += Q/LK ;//初始点边对应的信息素浓度}}p = 0xfffff;//虽然已经完成操作，但我们要直观的从所有现有路径中找出最短的路径。for(i = 0;i < m;i++){LK = 0;for(j = 0;j < n-1;j++)LK += D[Path[i][j]][Path[i][j+1]];//计算一次循环中蚂蚁的总路程LK += D[Path[i][j]][Path[i][0]];//回到初始点if(LK < p){p = LK;start = i;}}for(i = 0;i < n; i++)cout << Path[start][i]+1<<"->";cout << Path[start][0]+1<<endl;return 0;
}

 

三种算法的优缺点对比

算法

优势

不足

模拟退火算法有限度接受劣值，可求解非线性问题，鲁棒性强。运算速度慢，挠动机制种类繁多，易遗失当前最优解。
遗传算法具备并行搜索特性，且不受函数约束条件限制、全局搜索性能较强、获得局部最优的概率较低。计算量较大，占用存储空间存储空间较多。
蚁群算法编程简单、鲁棒性强、易于与其他算法结合、并行性好、适用领域广泛。搜索速度有待提高，且容易停滞而得到局部最优。

 

参考资料：

https://www.cnblogs.com/lyrichu/p/6688459.html

https://www.cnblogs.com/lyrichu/p/6152928.html

https://blog.csdn.net/shelldawn/article/details/80613132

https://www.cnblogs.com/8335IT/p/5635892.html

吴慧超，《基于ROS的多AGV多目标点导航系统研究及实现》

 

 

 

这篇关于自然启发的搜索算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/923765。

相关文章

黑神话：悟空》增加草地绘制距离MOD使游戏场景看起来更加广阔与自然，增强了游戏的沉浸式体验

黑神话：悟空》增加草地绘制距离MOD使游戏场景看起来更加广阔与自然，增强了游戏的沉浸式体验

《黑神话：悟空》增加草地绘制距离MOD为玩家提供了一种全新的视觉体验，通过扩展游戏中草地的绘制距离，增加了场景的深度和真实感。该MOD通过增加草地的绘制距离，使游戏场景看起来更加广阔与自然，增强了游戏的沉浸式体验。 增加草地绘制距离MOD安装 1、在%userprofile%AppDataLocalb1SavedConfigWindows目录下找到Engine.ini文件。 2、使用记事本编辑
阅读更多...
国自然！2025年立项最新动态汇总！（文末附模板）

国自然！2025年立项最新动态汇总！（文末附模板）

【SciencePub学术】8月23日，国自然基金委正式发布《关于2024年国家自然科学基金集中接收申请项目评审结果的通告》，根据公告，2024年基金委共接收项目申请384564项（2023年304333项），经初审和复审后共受理383126项（2023年303329项）。 本次小编汇总了已公布学科的立项建议通告，各学科领域征集截止时间各不相同，请仔细查收，文末附带立项建议模板！ 01
阅读更多...
受粘液启发的水凝胶是啥？有啥作用？

受粘液启发的水凝胶是啥？有啥作用？

大家好，今天我们来了解一篇关于粘液启发的自愈水凝胶的研究——《Mucus-Inspired Self-Healing Hydrogels: A Protective Barrier for Cells against Viral Infection》发表于《ADVANCED MATERIALS》。粘液是一种保护细胞的生物水凝胶，而这种水凝胶受其启发，具有独特的性质。它由特殊的共聚
阅读更多...
陈坤2024行走的力量启程 重归自然感受自我

陈坤2024行走的力量启程 重归自然感受自我

近日，由陈坤发起的心灵建设公益项目“行走的力量”发布2024宣传片，今年行走以“行止由心，自然生长”为主题，向大家传递希望在行走的过程中感受自我，自由生长，同时发出“你，为什么而出发”的提问，开启第14年的行走。 从2011年项目发起，到现在已经走了十四年，每次出发，都是全新的收获。陈坤和团队通过网络进行志愿者招募，和有心人一起同行，开启长达一周左右的行走，不仅是拥抱自然，更是为了在这个
阅读更多...
Fabric.js TextBox揭秘：splitByGrapheme属性实现文本自然换行

Fabric.js TextBox揭秘：splitByGrapheme属性实现文本自然换行

在Node.js的前端图形处理库中，Fabric.js是一个功能强大的库，允许开发者在HTML5的<canvas>元素上绘制和操作图形、图像和文本。然而，在Fabric.js中直接处理文本时，默认情况下文本并不会自动换行。为了实现文本的自动换行，Fabric.js提供了TextBox类，并通过splitByGrapheme属性来控制文本的换行行为。本文将深入解析splitByGrapheme属性的
阅读更多...
算法-搜索算法：二分查找（Binary Search）【前置条件：待查数据集必须是有序结构，可以右重复元素】【时间复杂度：O(logn)】

算法-搜索算法：二分查找（Binary Search）【前置条件：待查数据集必须是有序结构，可以右重复元素】【时间复杂度：O(logn)】

搜索：是在一个项目集合中找到一个特定项目的算法过程。搜索通常的答案是真的或假的，因为该项目是否存在。 搜索的几种常见方法：顺序/线性查找、二分法查找、二叉树查找、哈希查找 二分查找又称折半查找，优点是比较次数少，查找速度快，平均性能好；缺点是要求待查表： 必须采用顺序存储结构；必须按关键字大小有序排列；插入删除困难； 二分查找/折半查找方法适用于不经常变动而查找频繁的有序列表： 首先，假设
阅读更多...
各位天命人！国自然评审意见出来了，那如何判断是否上会？

各位天命人！国自然评审意见出来了，那如何判断是否上会？

公众号：生信漫谈，获取最新科研信息！ 各位天命人！国自然评审意见出来了，那如何判断是否上会？https://mp.weixin.qq.com/s?__biz=MzkwNjQyNTUwMw==&mid=2247487055&idx=1&sn=1dc8b66e10323d37e477e8829dad0c76&chksm=c0e9ebbff79e62a94fcd49341ae18cfe19aa3aa8
阅读更多...
知名专家郑茂林：SCDO主网与子网的交互自然系统在未来具有无限潜力

知名专家郑茂林：SCDO主网与子网的交互自然系统在未来具有无限潜力

2020年8月26日，SCDO全球区块链技术大会于深圳隆重启幕。SCDO资深顾问，互联网金融及大数据行业内领军人物郑茂林博士在会上做了重要演讲。 郑茂林强调：SCDO的分片技术可以实现交易速度的成倍增长 在会上，郑茂林对SCDO的算法与数据模型进行了具体解说，强调SCDO的分片技术可以实现交易速度的成倍增长，共识算法ZPoW的CPU绝对友好，主链协议可以使SCDO主网延伸到各个应用领域。郑博士
阅读更多...
团队动力之公平启发理论

团队动力之公平启发理论

不可不知的“公平启发理论” 公平启发理论‌主要用来回答如下问题： 公平感是如何产生的。公平感会对后续行为产生什么样的影响。 公平启发理论‌描述了人们在某个给定的情境下是如何构建自己的公平信念的，核心内容可以概括为两个阶段三个效应。两个阶段是指公平判断的形成和使用两个阶段。三个效应是指主因效应、替代效应以及其他效应。 两个阶段 ‌公平判断的形成阶段‌ 人们在日常生活中的决策更符合人们的生活实际
阅读更多...
旋转排序：搜索算法

旋转排序：搜索算法

搜索旋转排序数组的算法设计 引言 在计算机科学的世界中，二分搜索算法被广泛认为是处理已排序数组查找任务的高效工具。 它通过不断将搜索范围缩小一半的方式，快速定位到所需元素的位置，这种方法的时间复杂度仅为O(log n)，使得它在处理大型数据集时表现出色。 然而，这种传统方法面临一个显著的挑战：当数组经历旋转后，原有的排序顺序被打乱，二分搜索的效率和有效性便会大打折扣。 为了解决旋转排序数
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2