模拟退火（SA）搜索算法

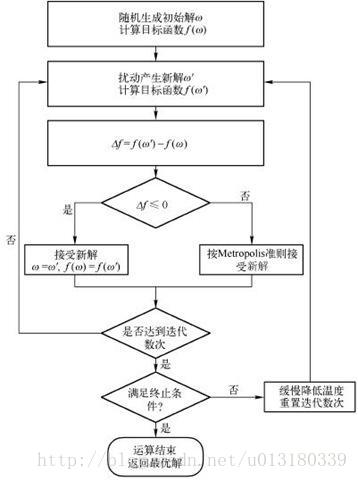
本文主要是介绍模拟退火（SA）搜索算法，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

所谓的爬山算法实际上就是简单的贪心算法，贪心算法通过从当前解的临近空间选择一个最优的解作为新的当前解，因此这个解很有可能是局部最优解，而不是全局最优的。因为A的领域周围没有比他更优的解了。

 

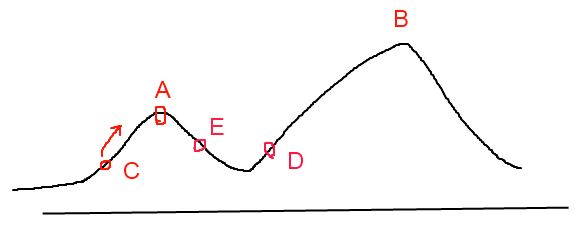
模拟退火搜索通过允许向不好的状态移动来避开局部最值点，但频率逐渐降低。它是一种基于蒙特卡洛思想设计的近似求解最优化问题的方法。

伪代码如下：

  choose an initial solution X0  randomly                      //随机的选择一个初始解X0
  give an initial temperature T0 , X ← X0, T ← T0       //初始化温度T0
  while the stop criterion is not yet satisfied do            //停止准则不满足则
   {   for i ← 1 to  L do                                                  //Markov 链的长度 L
        {  pick a solution  X'∈N(X) randomly                  //随机选择临域内一个解X'，为逃离局部最值点
           Δf ← f(X')-f(X)                                                   //后续节点-当前节点
           if Δf<0  then  X ← X'                                         
           else  X ← X' with  probability exp(- Δf/T)  }        //  以exp(- Δf/T)的接受概率接受X'
   T← g(T)    //generally, T ← aT    }                             //温度下降
  return X
 

void SimulatedAnnealing()

{

  蒙特卡洛随机产生一个初始解X0;

     初始化温度T、迭代次数L、降温系数TA、迭代误差E

      for(int i=0;i<L;i++)//退火过程

     {

     计算与新解所对应的目标函数差df;

     if(df<0)

        接受当前的解X′作为新解X;

     else

       以概率exp(-Δt′/T)接受X′作为新的当前解X;

     T = AT * T ; //降温退火

     }

}

 

#include<iostream>
#include<ctime>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<time.h>
#include<stdlib.h>
#include<stdio.h> 
//#include <windows.h>#define MAX 10000
#define INF 10000000 
#define E 0.000000001  // 迭代误差 
#define L 40000    // 迭代次数 
#define AT 0.999   // 降温系数 
#define T 1       // 初始温度 #define N 5//城市个数
using namespace std; struct element{     //用来排序的数据结构 int data;  // 数据 int index;  // 序号 
};int tsp(int d[][N], int n, double e,int l,double at,double t,int s0[]);  //利用模拟退火算法求解最短路径 
int cmp(const void *a,const void *b); //升序排列 
void rand_of_n(int a[],int n);  //产生 1-n 的随机排列并存到 a[] 中
int random(int m,int n);
//int dis[MAX][MAX];   // d[i][j] 表示客户i到客户j的距离，0 表示起始点 int dis[N][N]={0,1,57,20,81, 1,0,59,49,36, 57,59,0,90,82, 20,49,90,0,75, 81,36,82,75,0 };void rand_of_n(int a[],int n){int i;struct element ele[MAX];srand((int)time(0));  // 初始化随机数种子 for(i=0;i<n;i++){ele[i].data=rand();  // 随机生成一个数 ele[i].index=i+1;}qsort(ele,n,sizeof(ele[0]),cmp);  //排序 for(i=0;i<n;i++){a[i]=ele[i].index;}
}int random(int m,int n){   //产生m-n的随机数int a;double x=(double)rand()/RAND_MAX;a=(int)(x*(n-m)+0.5)+m;return a;
}	int cmp(const void *a,const void *b){   // 升序排序return((struct element*)a)->data - ((struct element*)b)->data;
}int tsp(int d[][N], int n, double e,int l,double at,double t,int s0[]){int i,j,s[N],sum,temp;sum=INF; for(i=0;i<1000;i++){  //利用蒙特卡洛方法产生初始解rand_of_n(&s[1],n);s[0]=0; s[n+1]=0;  //第一个和最后一个点为起始点 temp=0;for(j=0;j<=n;j++)temp=temp+d[s[j]][s[j+1]];if(temp<sum){for(j=0;j<=n+1;j++)s0[j]=s[j];sum=temp;} }for(i=0;i<l;i++){    //退火过程 int c1,c2;c1=random(1,n);c2=random(1,n);if(c1>c2){int temp=c2; c2=c1; c1=temp;} if(c1==c2)continue;int df=d[s0[c1-1]][s0[c2]] + d[s0[c1]][s0[c2+1]] - d[s0[c1-1]][s0[c1]] - d[s0[c2]][s0[c2+1]]; //计算代价函数if(df<0){  //接受准则while(c1<c2){ int temp=s0[c2]; s0[c2]=s0[c1]; s0[c1]=temp;c1++;c2--;}sum=sum+df;} else if(exp(-df/t)>((double)rand()/RAND_MAX)){while(c1<c2){int temp=s0[c2]; s0[c2]=s0[c1]; s0[c1]=temp;c1++;c2--;}sum=sum+df;}t=t*at;//线性降温if(t<e)break;}return sum;
}int main(){//DWORD start, stop;int i,j;int sum,sum0,s0[MAX]; sum0=0;   //顺序遍历时的路程 for(i=0;i<N;i++){sum0=sum0+dis[i][i+1];}sum0=sum0+dis[N][0];sum=tsp(dis,N, E,L,AT,T,s0);for(i=1;i<=N;i++)cout<<s0[i]<<" ";cout<<endl; 	printf("模拟节点个数 %d\n", N);return 0; 
}

缺点：收敛速度慢、不能保证得到全局最优值。

增加获得全局最优值的可能性：

1. 增加模拟运行的时间（迭代次数）;
2. 多次重新启动，重置所有变量并开始新的SA，从不同搜索区域的位置开始。

 

 

 

 

这篇关于模拟退火（SA）搜索算法的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---