本文主要是介绍Maximum subarray problem(“最大和子数组”问题)与Kadane’s algorithm，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！
最大和子串：在计算机科学中，最大子数组问题就是在给定一维数组中寻找和最大的连续的子数组，并确定起点索引i，终点索引j和最大和。（该定义翻译自wikipedia）
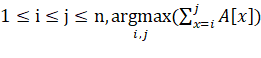
最直接的方法就是穷举每一个子串计算和：暴力搜索1(Brute force）
def findMaxSum(arr):n=len(arr)maxSum=arr[0]beginIndex=0endIndex=0for i in range(n):for j in range(i,n):tempSum=0for k in range(i,j+1):tempSum += arr[k]if maxSum<tempSum:maxSum=tempSumbeginIndex=iendIndex=jreturn maxSum,beginIndex,endIndex该算法复杂度为O(n^3)很容易发现，在确定子数组起点索引i后，j在增大的过程中求和运算存在大量冗余计算，故改进为：采用一个临时变量将从i到j的和保存下来，每次j增大时，这个临时变量只要加上一个数组值就行了：
def findMaxSum1(arr):n=len(arr)maxSum=arr[0]beginIndex=0endIndex=0for i in range(n-1):tempSum=0 #这里用临时变量存储i到j的和for j in range(i,n):tempSum += arr[j]if maxSum<tempSum:maxSum=tempSumbeginIndex=iendIndex=jreturn maxSum,beginIndex,endIndex该算法时间复杂度为O(n^2),还能不能继续优化？
分治（Divide & Conquer）：递归地将原问题二分得到子问题，直到子问题为只有一个元素的子数组为止。然后再把子问题归并，归并两个子数组时需要将子数组A的“最大和子数组”的和、子数组B的“最大和子数组”的和以及“AB合并数组”的“最大和子数组”的和三者进行比较得到最大值。（回忆一下归并排序中的分而治之的归并思维）
def findMaxSum2(arr,start,end):if start>=end:return arr[start],start,startmid=start+(end-start)//2maxSumLeft,beginLeftIndex,endLeftIndex=findMaxSum2(arr,start,mid)maxSumRight,beginRightIndex,endRightIndex=findMaxSum2(arr,mid+1,end)leftExtendMaxSum=leftExtendTempSum=0tempIndex1=0for i in range(mid,start-1,-1):leftExtendTempSum+=arr[i]if leftExtendTempSum>leftExtendMaxSum:leftExtendMaxSum=leftExtendTempSumtempIndex1=irightExtendMaxSum=rightExtendTempSum=0tempIndex2=0for i in range(mid+1,end+1):rightExtendTempSum+=arr[i]if rightExtendTempSum>rightExtendMaxSum:rightExtendMaxSum=rightExtendTempSumtempIndex2=imaxSum=leftExtendMaxSum+rightExtendMaxSumbeginIndex=tempIndex1endIndex=tempIndex2if maxSum<maxSumLeft:beginIndex=beginLeftIndexendIndex=endLeftIndexmaxSum=maxSumLeftif maxSum<maxSumRight:beginIndex=beginRightIndexendIndex=endRightIndexmaxSum=maxSumRightreturn maxSum,beginIndex,endIndex该算法的时间复杂度为O(nlogn)
下面来膜拜一下线性时间复杂的解决此问题的算法！！！
Kadane’s algorithm算法的intuition竟然是Dynamic Programme!!!
如果我们知道数组中以索引位置
对应元素
结尾的“最大和子数组”的和为
，那么以索引位置
对应元素
结尾的“最大和子数组”的和
为多少？或者说以
结尾的“最大和子数组”将以
结尾的“最大数组和”作为前缀。即：
因为该算法使用了最优子结构（在以每个位置结尾的最大和子数组是以一个更小且有所重叠的子问题来计算），可以看作是Dynamic Programme的一个应用,给大神跪了。
def findMaxSum3(arr):maxSum=-float("inf")beginIndex=0endIndex=0max_ending_here=maxSumcurrentStartIndex=currentEndIndex=0for currentEndIndex in range(0,len(arr)):max_ending_here+=arr[currentEndIndex]if max_ending_here>maxSum:maxSum,beginIndex,endIndex=max_ending_here,currentStartIndex,currentEndIndexif max_ending_here<0:max_ending_here=0currentStartIndex=currentEndIndex+1return maxSum,beginIndex,endIndex只返回最大值的版本更简洁，直接从维基百科上copy过来：
def max_subarray(A):max_ending_here = max_so_far = A[0]for x in A[1:]:max_ending_here = max(x, max_ending_here + x)max_so_far = max(max_so_far, max_ending_here)return max_so_far下面测试代码：
import numpy as np
arr=np.random.randint(-100,100,1000)
print(findMaxSum(arr))
print(findMaxSum1(arr))
print(findMaxSum2(arr,0,len(arr)-1))
print(findMaxSum3(arr))输出一致，时间消耗差别明显！！！
(1520, 219, 554)
(1520, 219, 554)
(1520, 219, 554)
(1520, 219, 554)
这篇关于Maximum subarray problem(“最大和子数组”问题)与Kadane’s algorithm的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！
