LeetCode - distinct-subsequences

本文主要是介绍LeetCode - distinct-subsequences，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目：

Given a string S and a string T, count the number of distinct subsequences of T in S.

A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie,"ACE"is a subsequence of"ABCDE"while"AEC"is not).

Here is an example:
S ="rabbbit", T ="rabbit"

Return3.

 

题意：

翻译过来的很绕口，让人难以理解。我个人的理解就是  删掉S字符串中的某个字符后可以有多少种方法使得S还与T相等。

 

解题思路：

这时候就需要一张图了（滑稽）图来自于牛客网某位仁兄

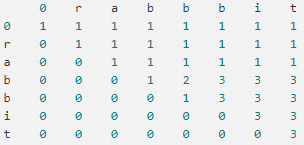
有图就好办了。

这题很明显使用动态规划来解决，我们以S.length()来做列，T.length()来做行 

动态规划一般有两个难点

第一个难点是如何确定边界，关于边界问题，可由上图得出，当T字符串为空时，所有次数都为1，当S字符串和T字符串都为空时，次数为1，当 S字符串为空，T不为空就全为0 ，好了边界已经确定好了

第二个难点是如何确定动态规划公式

S.charAt(j-1) = T.charAt(i-1)时，可以得出 array[i][j]  = array[i][j-1] +array[i-1][j-1];

S.charAt(j-1) != T.charAt(i-1)时   array[i][j] = array[i][j-1]

好了动态规划的公式也得出来了，现在就可以写代码了

 

需要注意的是：

遍历的时候不要从0开始，不然会出现空指针

i,j可以取到T,S的长度的，不然返回的值就是array数组最开始初始化的值 也就是0

 

代码如下：

	public int numDistinct(String S, String T) {if(S.length() == 0 && T.length() != 0) {return 0;}int[][] array = new int[T.length()+1][S.length()+1];//初始化边界for(int i = 0; i <= S.length(); i++) {array[0][i] = 1;}for(int j = 1; j <= T.length(); j++) {array[j][0] = 0;}for(int i = 1; i <= T.length(); i++) {for(int j = 1; j <= S.length(); j++) {if(S.charAt(j-1) == T.charAt(i-1)) {array[i][j] = array[i][j-1] + array[i-1][j-1];}else {array[i][j] = array[i][j-1];}}}return array[T.length()][S.length()];}

 

这篇关于LeetCode - distinct-subsequences的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---