超平实版Pytorch CNN Conv2d

本文主要是介绍超平实版Pytorch CNN Conv2d，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

torch.nn.Conv2d

基本参数

in_channels (int)
        输入的通道数量。比如一个2D的图片，由R、G、B三个通道的2D数据叠加。

out_channels (int)
        输出的通道数量。

kernel_size (int or tuple)
        kernel（也就是卷积核，也可以称为filter）的形状

bias (bool, optional)
        是否加上一个可学习的bias。 Default: True.

stride (int or tuple)
        卷积步长。

注：关于为什么kernel_size和stride可以有int、tuple两种表示方式

如果是int，就是对于高那条边、宽那条边应用一样的值。比如如果你的kernel是int，那就是一个正方形的kernel。
如果是tuple，则第1个值应用在高那条边上，第2个值应用在宽那条边上！

 

输入输出的形状

输入形状：
     $(N,C_{in},H,W)$
     $N$是batch size
    $C_{in}$是输出的通道数量
     $H$是2D input的高度
     $W$是2D input的宽度

输出形状：
     $(N,C_{out},H_{out},W_{out})$

 

公式

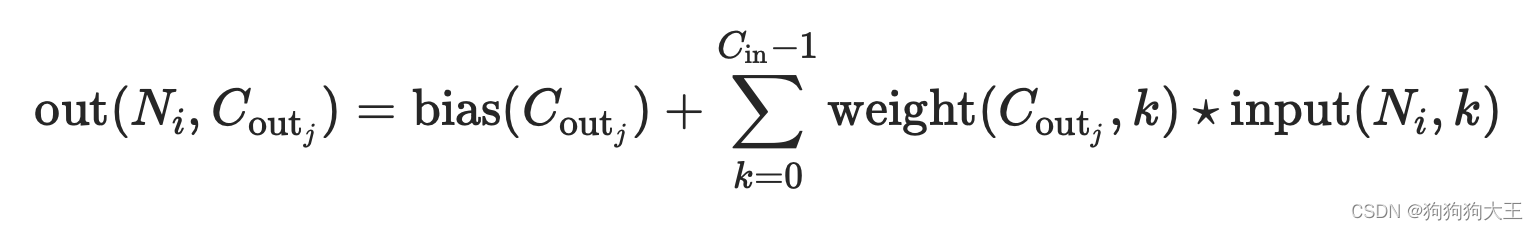
公式左边：
        $N$是batch size
        $C_{out}$是输出的通道
        (i, j)是索引

        所以这里的$out(N_i,{C_{out}}_j)$指的就是当前batch中第I个数据的第j个通道的情况。
        你就理解为，现在开始我们抛开batch不谈，且就看一个通道。

 
公式右边：
        五角星理解为一个操作
        $k$是在数数，从0数到$C_{in-1}$，也就是循环一遍input中的通道数量而已。

 

图例

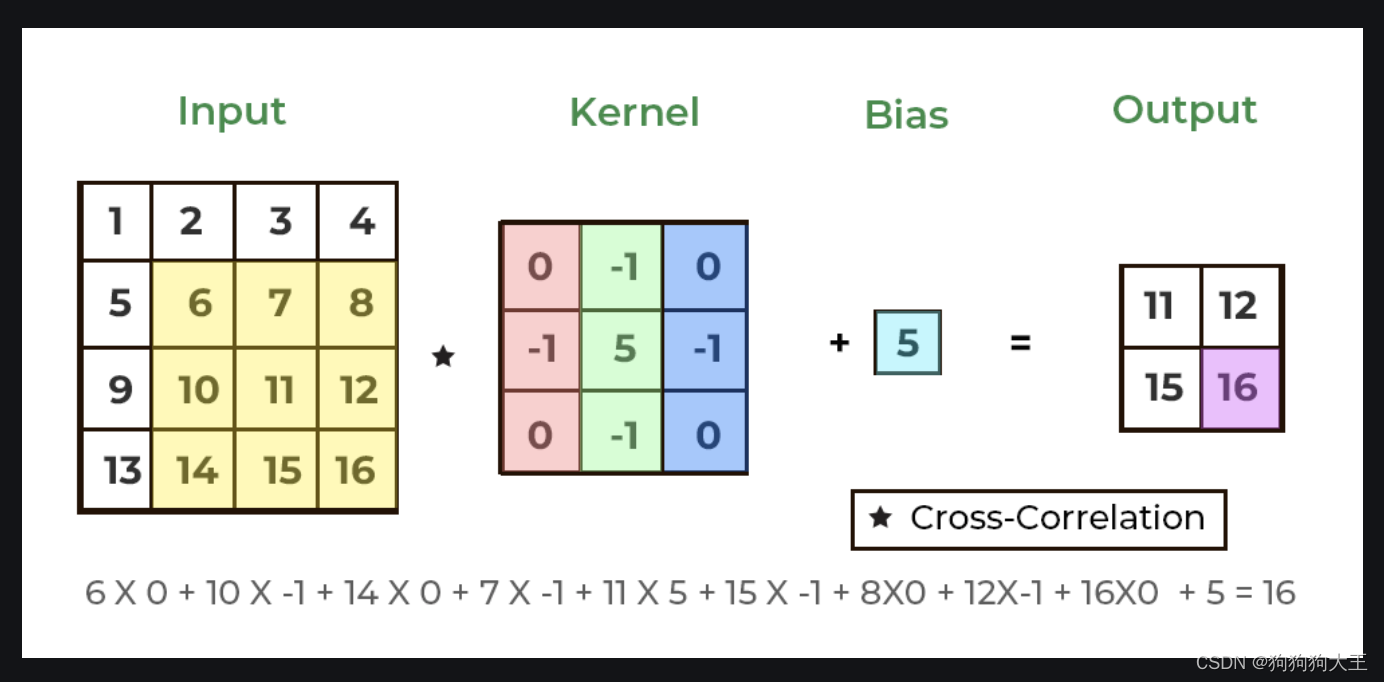
（图片引用自Apply a 2D Convolution Operation in PyTorch）

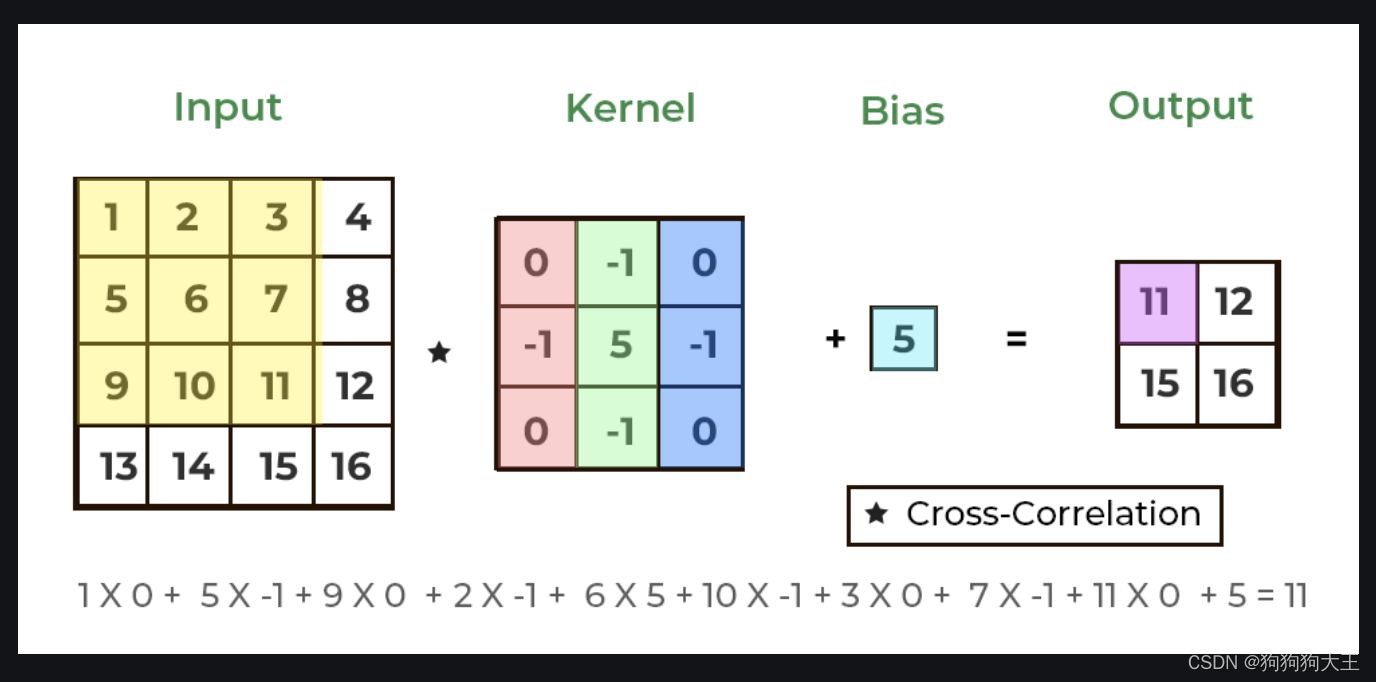
对于每一次kernel的移动：完全对应的位置，数字两两相乘，然后每一对的结果相加，最后加上bias。这里不确定为什么kernel画了三个颜色，我觉得可能只是表示下面计算的顺序是从左到右、从上到下写的。

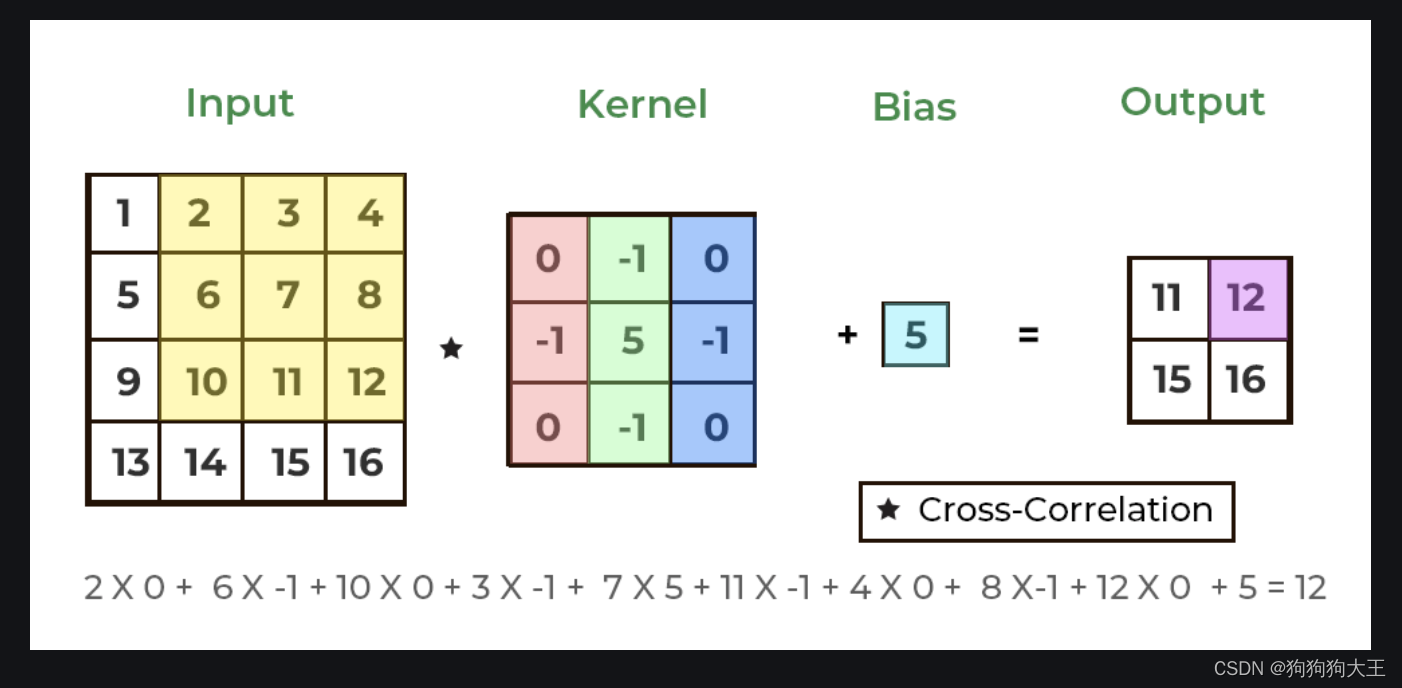
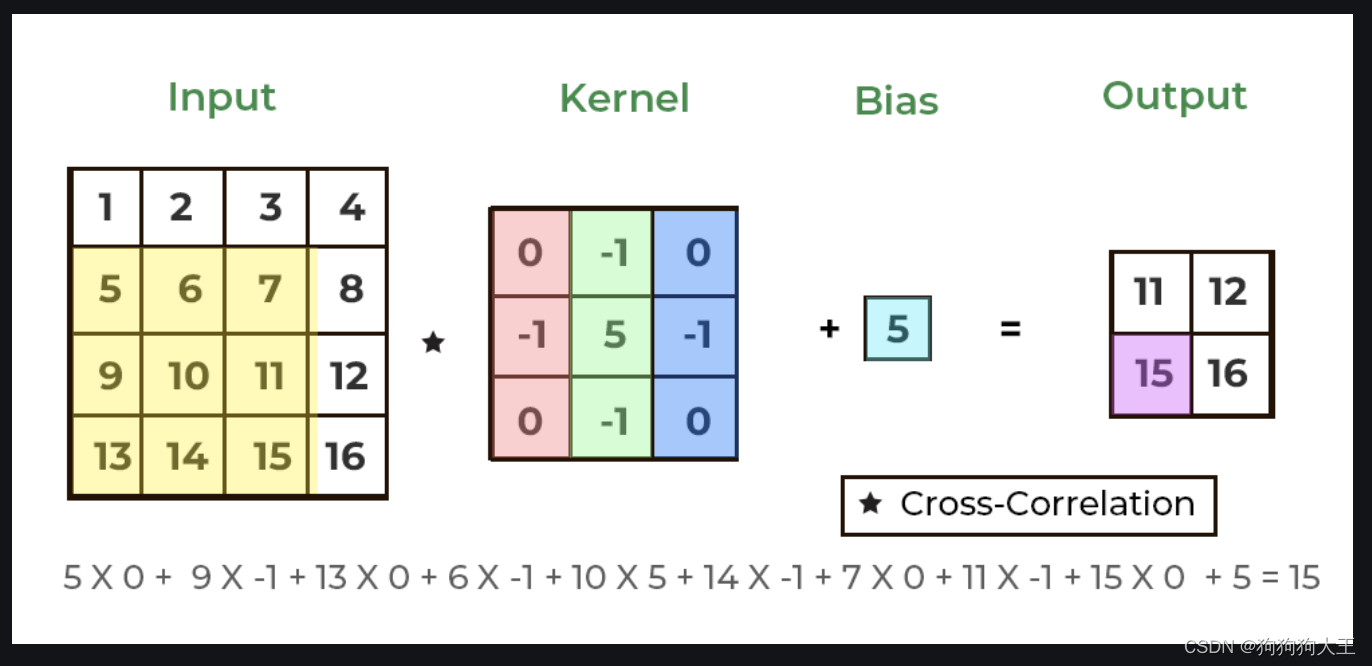
参考文档

1. Pytorch Conv2d文档
2. Apply a 2D Convolution Operation in PyTorch
3. PyTorch 2D Convolution

这篇关于超平实版Pytorch CNN Conv2d的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---