本文主要是介绍哈希表之处理哈希冲突的闭散列方式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
一. 哈希的概念
首先,在顺序搜索以及二叉树搜索树中,元素存储的位置与元素的关键码之间没有对应的关系,因此查找一个元素时,必须要经过关键码的多次比较,搜索效率取决于搜索过程中元素的比较次数。
那么,我们理想的搜索方法是:可以不经过任何的比较,一次直接从中找到要搜索的元素。如果构造一种存储结构,通过某种函数使得元素的存储位置与元素的关键码之间有一一映射的关系,那么在查找过程中通过该哈希函数可以直接找到该元素。当向该存储结构中:
(1)插入元素时:根据某种函数利用待插元素的关键码计算出该元素的存储位置并按照此位置进行存放。
(2)搜索元素时:根据某种函数利用待搜索元素的关键码计算出该元素应该存储的位置,在该位置取出元素与搜索元素比较,若相等时则表示搜索成功,否则搜索失败。
该方式即为哈希(散列)方法,哈希方法中使用的某种函数称为哈希(散列)函数,构造出来的存储结构称为哈希(散列)表。
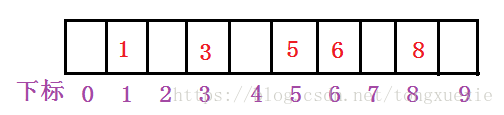
举例:数据集合={1,3,5,6,8} 哈希函数:Hash(key)=key%10
此时,将数据集合中的元素存储在哈希表中如下:
将key值代入到哈希函数中,从而取出该key值的存储位置,此时,搜索指定元素如8时,直接利用哈希函数计算出存储位置下标,将其对应的值与要搜索的值8比较,相等时,表示找到了,否则没找到。通过上述操作可以看出,搜索的速度非常快。
但存在这样一个问题:当向数据集合中插入元素11时,将元素11存储在哪儿?依旧利用key=11计算出Hash(11)=11%10=1,那么原本应该存储在下标为1的位置,但是此时下标为1的位置已经有存储的元素1,对于出现的这种现象我们称为哈希冲突!
哈希冲突:对于两个数据元素的关键码Ki和Kj(i!=j),即Ki!=Kj,有Hash(Ki)==Hash(Kj),即不同的关键码通过相同的哈希函数计算得到相同的哈希地址,这种现象称为哈希冲突或哈希碰撞。把具有不同关键码而计算出相同的哈希地址的数据元素称为同义词。那么发生这种哈希冲突应该如何处理呢?
处理哈希冲突常见有两种解决方式:闭散列和开散列。
二.闭散列处理哈希冲突
闭散列:也叫开放地址法,当发生哈希冲突时,如果哈希表未被装满,说明哈希表中必然还有空位置,那么就可以把key存放在表中的“下一个”空位中。那如何寻找下一个空位置呢?
我们介绍以线性探测的方式寻找下一个空位置。下面举例介绍如何线性探测寻找下一个空位置去处理哈希冲突:
这篇关于哈希表之处理哈希冲突的闭散列方式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!