本文主要是介绍灰太狼的数据世界(四),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!

Scipy是
一个专门用于科学计算的库
它与Numpy有着密切的关系
Numpy是Scipy的基础
Scipy通过Numpy数据来进行科学计算
包含
统计
优化
整合
以及线性代数模块
傅里叶变换
信号和图像图例
常微分方差的求解等
给个表给你参考下?

怎么样?
是不是看上去就有一股很骚气的味道?
那咱就继续学下去呗!
首先
安装
个人推荐pip直接全家桶
pip install -U numpy scipy scikit-learn

当然也有人推荐
Anaconda
因为用了它
一套环境全搞定
妈妈再也不用担心我安装问题了~
安装完之后就是直接使用了
首先我们来谈谈
(这些函数其实都是numpy里面的
它们也可以被scipy对象使用)
unique函数
之前在numpy里面有说过
主要是用来除去重复元素
同样的,这个方法适用numpy
也适用于sm这样的一个对象
(类似于python里面的set)
import numpy as np
import scipy.misc as sm
x = np.array([1, 3, 2, 1, 4, 2])
print(np.unique(x), "# unique(x)")
face = sm.face()
print(np.unique(face), "# unique(face)")
bincount函数
统计出数组里的从0到数组最大值n
共n+1个自然数出现的次数
具体做法
先找出数组里的最大值
统计0~最大值间的所有值出现的次数
import numpy as np
import scipy.misc as sm
ascent = sm.ascent()
print("max of array {} has {}"
.format(np.max(ascent[0]),
len(ascent[0])))
b = np.bincount(ascent[0])
print("return array's length {}"
.format(len(b)))
print("result {}".format(b))
fromfunctiont函数
类似于python里面的map函数
利用传入的函数生成一个数组
import numpy as np
def func(x, y):
return (x + y) * 3
t = np.fromfunction(func, (3, 4),
dtype=np.uint8)
print( "t = {}".format(t))
除了上面这几个
还有下面几个函数
put函数
替换数组里面的值
putmask函数
和put一样,也是替换
.........
刚刚说的这些
还是停留在Numpy的基础上
都是Numpy自己的函数
下面我们来说点有用的
看看Scipy自己的函数吧~
Scipy有一些专门的类
可以用来创建
稀疏矩阵
coo_matrix
csc_matrix
csr_matrix
bsr_matrix
我们来瞧一个栗子
import numpy as np
import scipy.sparse as ss
a = np.zeros((3, 4))
a[1, 2] = 12
a[2, 2] = 22
print(a)
print(ss.csc_matrix(a))

我们可以在创建的ndarry里面找出不为零的值和他的位置,
将这个数组直接转化成稀疏矩阵
我们还可以利用
mat函数/bmat函数
来创建特殊的矩阵
np.mat函数可将数组转为矩阵
np.bmat函数可以矩阵为参数创建阵列的矩阵
import numpy as np
a = np.mat(np.ones([3, 3]))
b = np.mat(np.zeros([3,3]))
print("a = {}".format(a))
print("b = {}".format(b))
c = np.bmat("a,b;b,a")
print("c = {}".format(c))
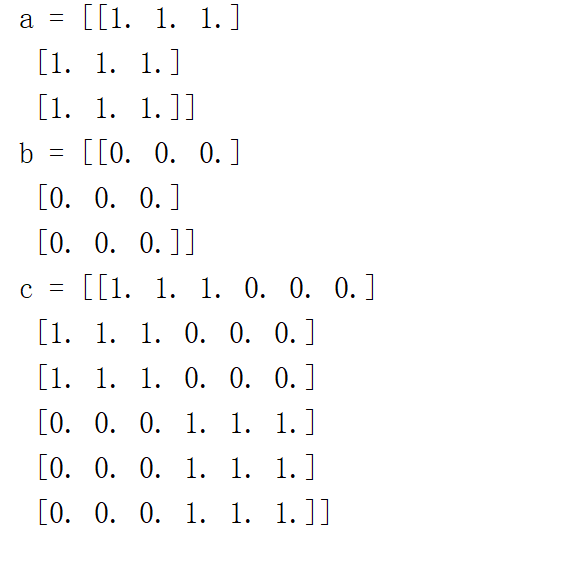
Tile函数
将第一个参数映射到第二个参数
import numpy as np
t = np.arange(9).reshape([3, 3])
print(t)
tm = np.tile(t, [3,2])
print(tm)
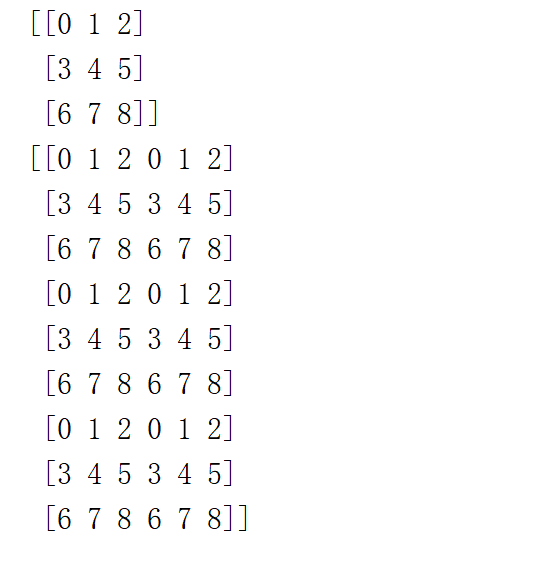
将t映射到【3,2】上
block_diag函数
block_diag函数可以创建一个
广义“主对角线”非0的大矩阵
其参数是矩阵
用矩阵作为主对角线性的值
所以矩阵会很大~
import numpy as np
import scipy.linalg as sl
a = np.mat(np.ones([3, 3]))
b = np.mat(np.ones([4, 3]))
c = np.mat(np.ones([3, 4]))
print("a = {}".format(a))
print("b = {}".format(b))
print("c = {}".format(c))
d = sl.block_diag(a,b,c)
print("d = {}".format(d))
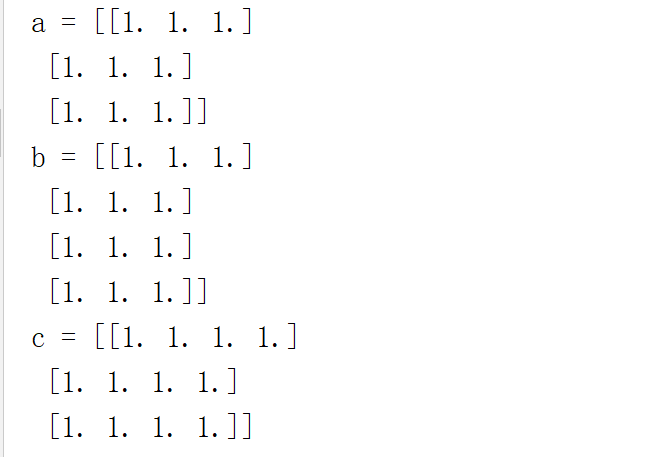
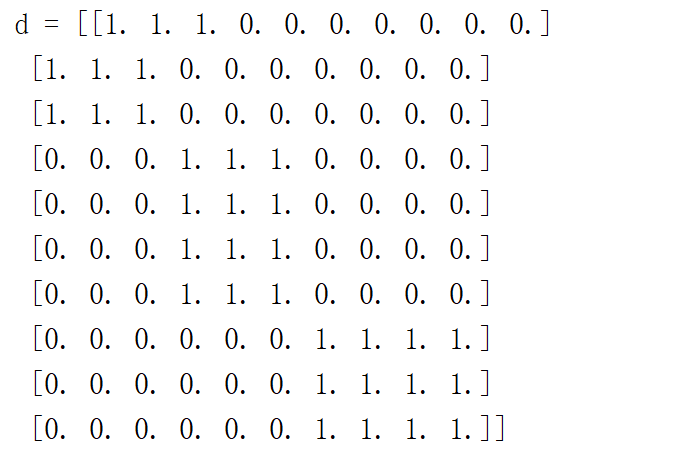
除了创建矩阵
scipy当然还有更多有趣的地方
例如
对线性方程组求解
具体怎么算的我也就不瞎说了
图能看懂就看
高数没学好的
推荐一个重新学的网址:
https://baike.baidu.com/item/lu%E5%88%86%E8%A7%A3/764245?fr=aladdin
我们有各种方法进行求解
例如:
LU分解
QR分解
SVD分解
Cholesky分解
先来了解一下LU分解~

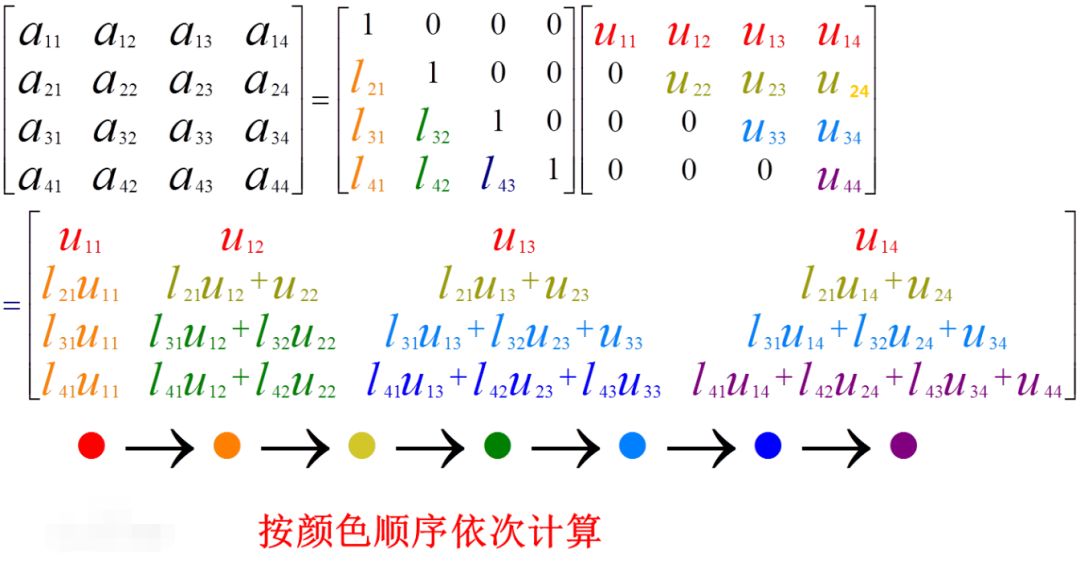
将LU分解转化成Scipy代码
SciPy里的
scipy.linalg.lu函数可以基本实现对Ax=b的LU分解
但scipy.linalg.lu函数的返回值有三个p'、l'、u'
所以矩阵分解变为(P'L')U' = A
from scipy.linalg import lu
import numpy as np
A = np.matrix([[2,3],[5,4]])
b = np.matrix([4,3])
p,l,u = lu(A)
print("p = {}".format(p))
print("l = {}".format(l))
print("u = {}".format(u))
print("plu = {}".format(p.dot(l).dot(u)))
print("A = {}".format(A))
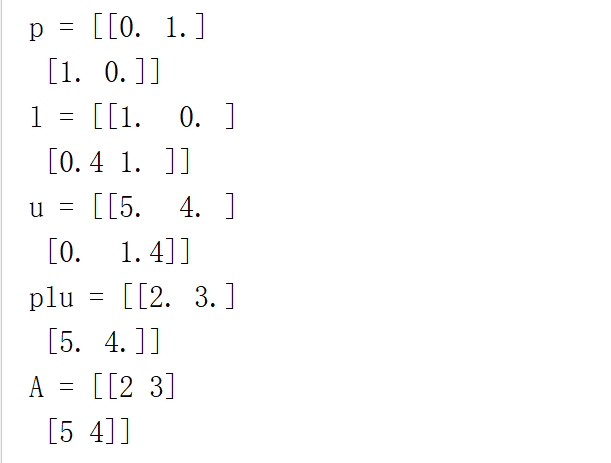
下面我们可以利用
LU分解求方程组的解
分解过后的方程如下:
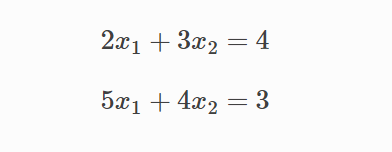
对应的结果也就是A
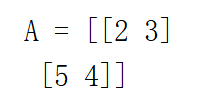
之后我们
求p、l、u
然后用pl和b求y
用u和y求x的值
from scipy.linalg import lu,solve
import numpy as np
A = np.array([[2,3],[5,4]])
b = np.array([4,3])
# 求的p l u
p,l,u = lu(A)
print("p = {}".format(p))
print("l = {}".format(l))
print("u = {}".format(u))
# 求ply = b的y
y = solve(p.dot(l), b)
print("y = {}".format(y))
# 求ux = y的x
x = solve(u, y)
print("x = {}".format(x))

结果最后一行输出的是x的值,
即
x=(x1,x2)=(−1,2)
Cholesky分解
要求解线性方程组Ax=b
其中为对称正定矩阵
又叫平方根法
是求解对称线性方程组常用的方法之一
那么可通过下面步骤求解
(1)求的Cholesky分解,得到A=LLT
(2)求解Ly=b,得到y
(3)求解LTx=y,得到x
下面使用
scipy.linalg模块下的cholesky函数
来对系数矩阵进行求cholesky分解
from scipy.linalg import cholesky
import numpy as np
from scipy.linalg import lu,solve
A = np.array([[1,2,3],[2,8,8],[3,8,35]])
b = np.array([1,8,20])
l = cholesky(A, lower=True)
print("L = {}".format(l))
print("matmul = {}".format(np.matmul(l,l.T)))
print("dot = {}".format(l.dot(l.T)))
y = solve(l, b)
print(l.dot(y), b)
x = solve(l.T, y)
print("x = {}".format(x))
print(l.T.dot(x), y)
print("y = {}".format(y))

QR分解
QR分解法是三种将矩阵分解的方式之一
它把矩阵分解成:
一个正交矩阵与一个上三角矩阵的积
QR分解经常用来解线性最小二乘法问题
scipy.linalg模块下的qr函数
可以对矩阵进行QR分解操作
from scipy.linalg import qr
import numpy as np
aa = np.array([[0,3,1],[0,4,-2],[2,1,2]])
qq, rr = qr(aa)
print("Q = {}".format(qq))
print("R = {}".format(rr))
print("A = {}".format(aa))
print("QR = {}".format(qq.dot(rr)))
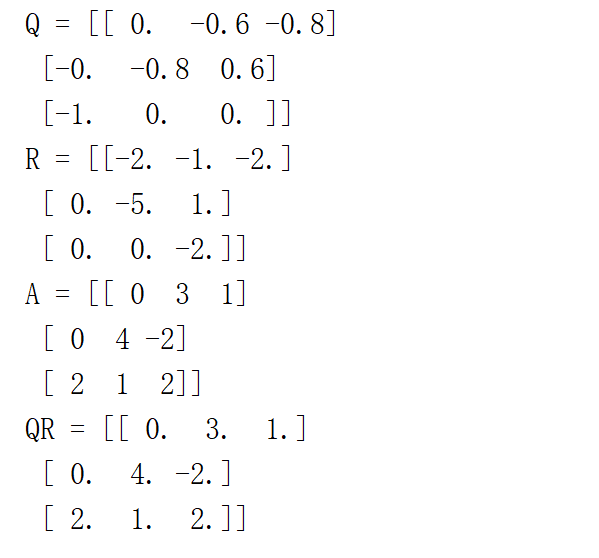
SVD奇异分解
svd是现在比较常见的算法之一
也是数据挖掘工程师、算法工程师
必备的技能之一
假设A是一个M×N的矩阵,
那么通过矩阵分解将会得到
U,Σ,VT(V的转置)三个矩阵
其中U是一个M×M的方阵
被称为左奇异向量
方阵里面的向量是正交的
Σ是一个M×N的对角矩阵
除了对角线的元素其他都是0
对角线上的值称为奇异值
VT(V的转置)是一个N×N的矩阵
被称为右奇异向量
方阵里面的向量也都是正交的
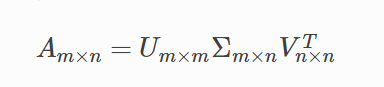
from scipy.linalg import qr,svd
import numpy as np
aa = np.array([[0,3,1],[0,4,-2],[2,1,2]])
u, e, v = svd(aa)
print("u = {}".format(u))
print("e = {}".format(e))
print("v = {}".format(v))

SVD的应用场景也比较明显
典型的使用的场景:
信号的降噪
图像的压缩
我们这边可以来看一个图像压缩的例子:
import scipy.misc
from scipy.linalg import svd
import matplotlib.pyplot as plt
import numpy as np
import numpy
img = scipy.misc.face()[:,:,0]
print(img.shape,type(img))
img = np.matrix(img)
U,s,Vh=svd(img)
plt.gray()
plt.subplot(221,aspect='equal')
plt.title("orignal")
plt.imshow(img)
plt.imsave('org.png', img)
A = numpy.dot(U[:,0:10],numpy.dot(numpy.diag(s[0:10]),Vh[0:10,:]))
plt.subplot(222,aspect='equal')
plt.title(":10")
plt.imshow(A)
plt.imsave('a10.png', A)
A = numpy.dot(U[:,0:50],numpy.dot(numpy.diag(s[0:50]),Vh[0:50,:]))
plt.subplot(223,aspect='equal')
plt.title(":50")
plt.imshow(A)
plt.imsave('a50.png', A)
A = numpy.dot(U[:,0:100],numpy.dot(numpy.diag(s[0:100]),Vh[0:100,:]))
plt.subplot(224,aspect='equal')
plt.title(":100")
plt.imshow(A)
plt.imsave('a100.png', A)
plt.show()
压缩原理如下:

总结
svd分解在
机器学习
深度学习
计算机视觉等领域
都有很多涉及
需明白基础不牢靠
学习机器学习也就是浮于表面
这一期关于scipy使用的内容就到这里了(主要是讲的如何去使用scipy,但是具体的数学理论没有特别去讲,觉得以后有必要搞一期,谈谈线性代数,毕竟矩阵这个东西我们现在很常用)
下一期我们将接触:
Scipy里面的
范德蒙多项式逼近
最邻近插值法
拉格朗日插值法
埃米尔特插值法
样条插值
函数的求导和积分
“看看数学,再看看python,再一脸懵逼”
这篇关于灰太狼的数据世界(四)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





