本文主要是介绍处女座算法之大整数乘法(从O(N^2)到O(N^1.59)的思想),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
每次看算法的优化设计都会觉得:优化算法的人都是处女座!
《算法设计与分析》一书讲完分治之后顺手讲了大数乘法的分治递归算法,然后又兴冲冲地将原本O(N^2)的算法优化成O(N^1.59)
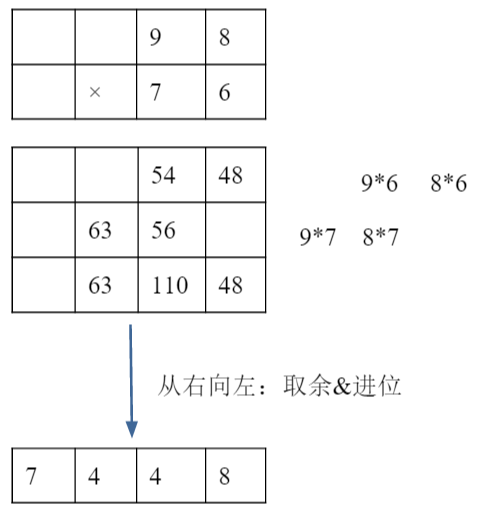
小学生是这样做乘法的:
让计算机模拟这个过程:
package com.mustso.java2;import java.util.Scanner;public class BigIntMultiply {final static int base = 10;//十进制数final static int N = 100;public static String bigIntMultiply(String A,String B){//首先考虑负数int t = 0;if (A.charAt(0)=='-'){++t;A = A.substring(1);}if (B.charAt(0)=='-'){++t;B = B.substring(1);}int [] C = new int[N];/** 计数器i:B从个位向高位遍历* 计数器j:A从个位向高位遍历* 计数器k+l:数组C保存的结果,C[0]保存结果的个位*/for (int i = B.length()-1,k = 0;i >= 0;--i,++k){for (int j = A.length()-1,l = 0;j >= 0;--j,++l){C[k+l]+=(int)(A.charAt(j)-'0')*(B.charAt(i)-'0');}}/** 说明:一个a位数乘以一个b位数的结果只可能是(a+b)位数或(a+b-1)位数* 比如:99*99 = 9801//2位数乘2位数最大是4位数* 10*10 = 100 //2位数乘2位数最小是3位数*///进位&取余for (int i = 0;i < A.length()+B.length()-1;++i){C[i+1]+=C[i]/base;C[i]%=base;}Stri这篇关于处女座算法之大整数乘法(从O(N^2)到O(N^1.59)的思想)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!