P4159 [SCOI2009] 迷路（矩阵快速幂，两点路径为k的方案数）

本文主要是介绍P4159 [SCOI2009] 迷路（矩阵快速幂，两点路径为k的方案数），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

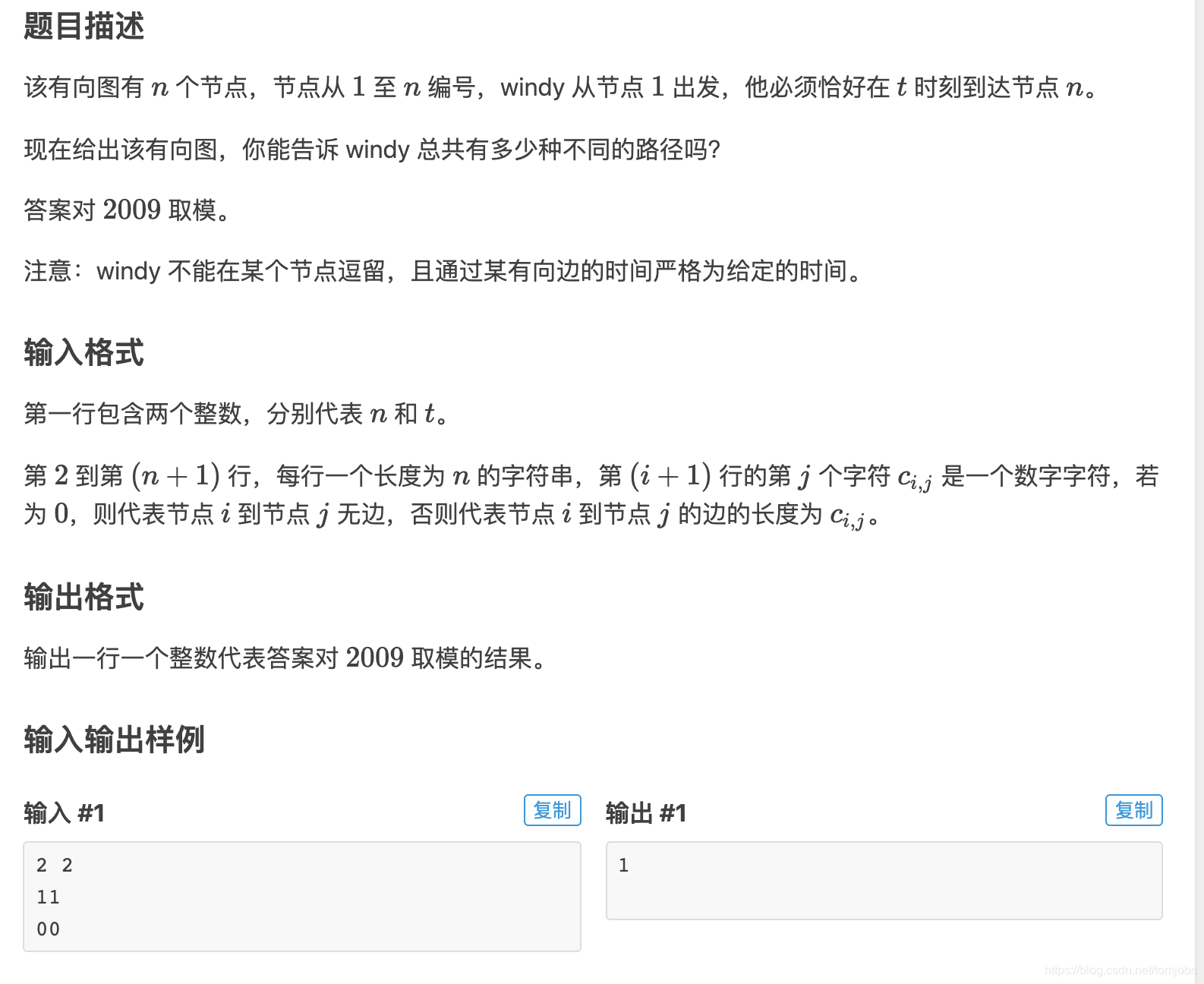
思路：
具体参考https://www.luogu.com.cn/blog/qq-2056188203/mi-lu-scoi2009-ti-xie

简而言之，就是如果权值为1，要求两点之间经过$k$条边的路径方案数，只要将邻接矩阵进行$k$次方就好了。
本题权重为1~9，我们将每个点拆成10个点，两个点边权就通过拆成的点建边来表示，这样就成了权值为1的邻接矩阵形式了。

#include <cstdio>
#include <cstring>
#include <algorithm>
#include <vector>
#include <map>using namespace std;typedef long long ll;const int INF = 0x3f3f3f3f;
const int maxn = 107;
const int mod = 2009;
int n,t;struct Matrix {int Ma[maxn][maxn];void clear() {memset(Ma,0,sizeof(Ma));}
}A;Matrix Mul(Matrix m1,Matrix m2) {Matrix now;now.clear();for(int i = 1;i <= n;i++) {for(int j = 1;j <= n;j++) {for(int k = 1;k <= n;k++) {now.Ma[i][j] = (now.Ma[i][j] + m1.Ma[i][k] * m2.Ma[k][j]) % mod;}}}return now;
}Matrix Qpow(Matrix a,int b) {Matrix now;now.clear();for(int i = 1;i <= n;i++) now.Ma[i][i] = 1;while(b) {if(b & 1) now = Mul(now,a);a = Mul(a, a);b >>= 1;}return now;
}int f(int i,int j) {return (i - 1) * 10 + j;
}int main() {scanf("%d%d",&n,&t);int N = n;n *= 10;for(int i = 1;i <= N;i++) {for(int j = 1;j < 10;j++) {A.Ma[f(i,j)][f(i,j + 1)] = 1;}for(int j = 1;j <= N;j++) {int x;scanf("%1d",&x);if(x) {A.Ma[f(i,x)][f(j,1)] = 1;}}}A = Qpow(A, t);printf("%d\n",A.Ma[f(1,1)][f(N,1)]);return 0;
}

这篇关于P4159 [SCOI2009] 迷路（矩阵快速幂，两点路径为k的方案数）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---