The 0-1 Knapsack Problem KNAPSACK

本文主要是介绍The 0-1 Knapsack Problem KNAPSACK，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

       Let U = {u1, u2, . . . , un} be a set of n items to be packed in a knapsack of size C. For 1 ≤ j ≤ n, let sj and vj be the size and value of the jth item, respectively. Here C and sj, vj , 1 ≤ j ≤ n, are all positive integers. Each item should either be placed entirely in the knapsack or no.

        The objective is to fill the knapsack with some items from U whose total size is at most C and such that their total value is maximum(the knapsack cannot contain more than one item of the same type).

  V(i,0)=0

      V(0,j)=0

      if  i>0 and j<si ,   V(i,j)=V(i-1,j)

       if  i>0 and j³si , V(i,j)=max{V(i-1,j),V(i-1,j- si)+ vi}

         We use an (n + 1) × (C + 1) table to evaluate the values of V [i, j]. We only need to fill the table V[0..n, 0..C] row by row using the above formula. The method is formally described in Algorithm knapsack.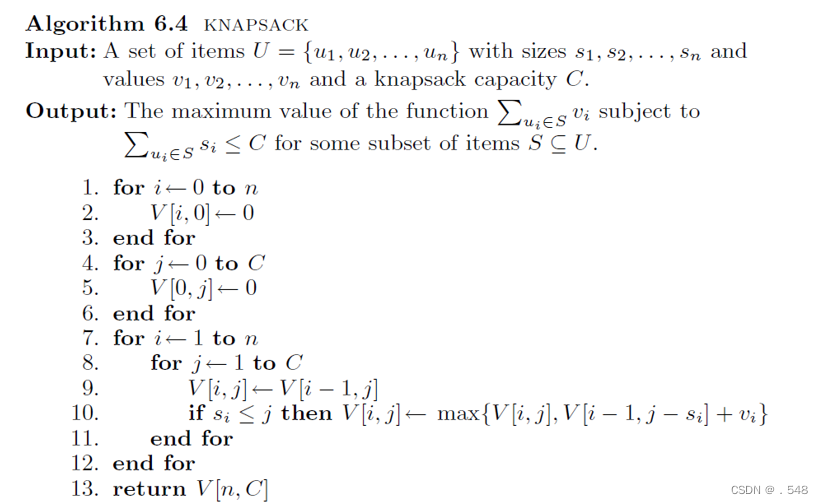

1. 首先，对于每个物品 i，初始化一个二维数组 V，其中 V[i, j] 表示在考虑前 i 个物品，并且背包容量为 j 时可以获得的最大价值。

2. 然后，对于每个物品 i 和背包容量 j，通过以下方式更新 V[i, j]：

   • 如果当前物品 i 的大小 s 小于等于背包容量 j，则 V[i, j] 的最大值为 V[i-1, j]（不放入当前物品 i）和 V[i-1, j-s] + v[i]（放入当前物品 i）中的较大值。
   • 如果当前物品 i 的大小 s 大于背包容量 j，则 V[i, j] 等于 V[i-1, j]（不能放入当前物品 i）。

3. 最后，返回 V[n, C]，即考虑了所有物品后，在背包容量为 C 时可以获得的最大价值。算法的时间复杂度是 O(nC) 空间复杂度O(c)

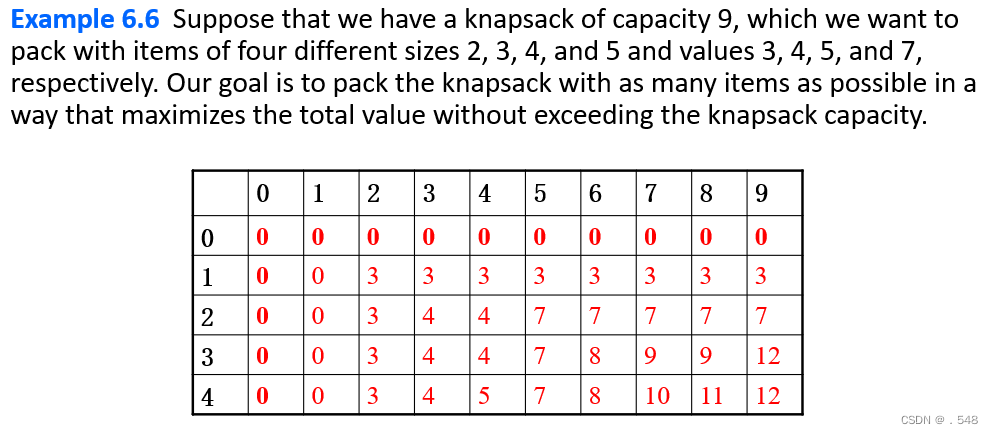【动态规划】01背包问题（通俗易懂，超基础讲解）_动态规划01背包问题-CSDN博客

【动态规划】背包问题_哔哩哔哩_bilibili

这篇关于The 0-1 Knapsack Problem KNAPSACK的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---