本文主要是介绍栈、队列、树——知识简单概括,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
(个人学习笔记,仅按个人想法所写,仅供参考)
1.栈
栈又名堆栈(stack),它是一种运算受限的线性表。限定仅在表尾进行插入和删除操作的线性表。这一端被称为栈顶,相对地,把另一端称为栈底。向一个栈插入新元素又称作进栈、入栈或压栈,它是把新元素放到栈顶元素的上面,使之成为新的栈顶元素;从一个栈删除元素又称作出栈或退栈,它是把栈顶元素删除掉,使其相邻的元素成为新的栈顶元素。
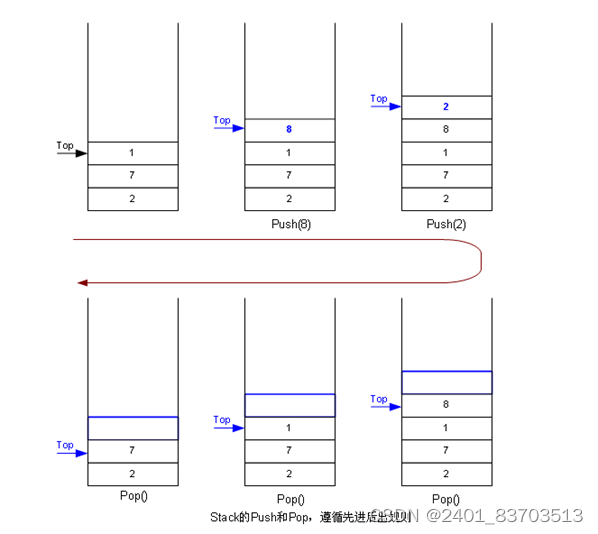
Push表示入栈,Pop表示出栈
通常称插入、删除的这一端为栈顶(Top),另一端称为栈底(Bottom)。
当表中没有元素时称为空栈。
栈为后进先出(Last In First Out)的线性表,简称为LIFO表。
栈的修改是按先进后出,后进先出的原则进行。每次删除(退栈)的总是当前栈中"最新"的元素,即最后插入(进栈)的元素,而最先插入的是被放在栈的底部,要到最后才能删除。
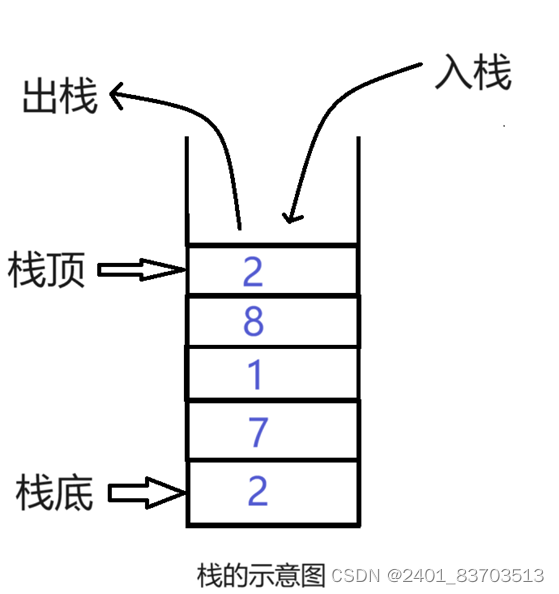
上图元素以2、7、1、8、2的顺序进栈,出栈的次序为2、8、1、7、2;
在出栈取元素的时候要分析栈内数据是否取完,可以判断栈顶的指针域是否为NULL;如果为NULL,可以return;
顺序栈的相关代码操作:(在这个代码中,利用数组存储数据,只能存6个数,通过地址传参,可以直接对指针指向的空间进行相关的赋值)
#include <stdio.h>
/*顺序栈的使用*/
struct STACK{int num[6];//整型数组int top;};//定义结构体
//函数声明
void Push_Stack(struct STACK *s);//地址传递,可以直接对指针指向的空间赋值
void Pop_Stack(struct STACK *s);
int Menu(void);int main()
{struct STACK sta={0};//定义局部变量sta.top=-1;//struct STACK sta={.top=-1};while(1){int num1=Menu();switch(num1){case 1:Push_Stack(&sta);break;case 2:Pop_Stack(&sta);break;case 0:return 0;}}return 0;
}
//目录
int Menu(void)
{int num1=0;printf("1.入栈\n");printf("2.出栈\n");printf("0.退出\n");scanf("%d",&num1);getchar();return num1;
}
//出栈
void Pop_Stack(struct STACK *s)
{if(s->top==-1)//判断栈是否已经取完{printf("栈已取空\n");return;}//代码到此说明栈还有数据printf("数据:%d\n",s->num[s->top]);(s->top)--;return;
}
//入栈
void Push_Stack(struct STACK *s)
{if(s->top==5)//判断栈是否已经存满,只能存6个数{printf("栈已存满\n");return;}//代码到此说明栈可以存数据(s->top)++;printf("请输入要入栈的数据:\n");scanf("%d",&(s->num[s->top]));getchar();printf("入栈成功\n");return;
}
链表栈的相关代码操作:
#include <stdio.h>
#include <stdlib.h>
/*链表栈的使用*/
struct NODE{int num;struct NODE *front;
};//定义结构体,定义成全局变量,方便其他的子函数使用//函数的声明
int List(void);
void Push_Stack(struct NODE **top);
void Pop_Stack(struct NODE **top);int main()
{struct NODE *top=NULL;//定义局部变量printf("栈的读和取\n");while(1){switch(List()){case 1:Push_Stack(&top);break;case 2:Pop_Stack(&top);break;case 0:return 0;}}return 0;
}
//目录
int List(void)
{int n=0;printf("1.入栈\n");printf("2.出栈\n");printf("0.退出\n");scanf("%d",&n);getchar();return n;
}
//出栈
void Pop_Stack(struct NODE **top)
{struct NODE *del=NULL;if((*top)==NULL){printf("栈为空\n");return;}//运行到此说明栈中还有数据printf("取出储存的数据:");printf("%d\n",(*top)->num);//打印数据del=*top;//把top暂存到del节点中(*top)=((*top)->front);//令原来top节点front地址中的节点等于新的topfree(del);//释放del节点,完成删除return;
}
//入栈
void Push_Stack(struct NODE **top)//传入top数据类型为struct NODE *,指针的命名为指针指向空间的数据类型 *所以格式为struct NODE **top
{struct NODE *new=(struct NODE *)malloc(sizeof(struct NODE));//创建新的节点new->front=NULL;//新节点的指针域为空printf("需要储存的数据\n");scanf("%d",&new->num);//传入数据到new节点的数据域num;getchar();new->front=(*top);//new节点的指针域指向top节点(*top)=new;//另new节点成为新的top,以此类推return;
}2.队列
队列(Queue)是只允许在一端进行插入,而在另一端进行删除的运算受限的线性表。
(1)允许删除的一端称为队头(Front)。
(2)允许插入的一端称为队尾(Rear)。
(3)当队列中没有元素时称为空队列。
(4)队列亦称作先进先出(First In First Out)的线性表,简称为FIFO表。
队列的修改是依先进先出的原则进行的。新来的成员总是加入队尾(即不允许"加塞"),每次离开的成员总是队列头上的(不允许中途离队),即当前"最老的"成员离队。
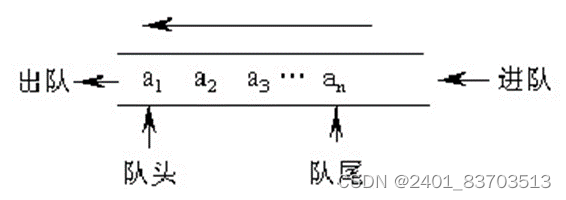
顺序队列:队列的顺序存储结构称为顺序队列。它是运算受限的顺序表。
循环队列:将向量空间想象为一个首尾相接的圆环,并称这种向量为循环向量。存储在其中的队列称为循环队列(Circular Queue)。
链队列:队列的链式存储结构称为链队列,如图3.16所示。一个链队列显然需要两个指针才能唯一确定,它们分别指示队头和队尾(分别称为头指针和尾指针)。与线性表的单链表一样,为了操作方便起见,我们也给链队列添加了一个头结点,并令头指针指向头结点.由此,空的链队列的判别条件为头指针和尾指针均指向头结点,如图3.17(a)所示。
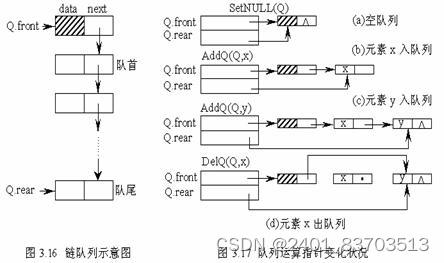
队列采用链表存储结构时,需要两个指针才能唯一确定,它们分别指示队头和队尾(分别称为头指针和尾指针)。
注意:
①和链栈类似,无须考虑判队满的运算及上溢。
②在出队算法中,一般只需修改队头指针。但当原队中只有一个结点时,该结点既是队头也是队尾,故删去此结点时亦需修改尾指针,且删去此结点后队列变空。
③和单链表类似,为了简化边界条件的处理,在队头结点前也可附加一个头结点,增加头结点的链队列的基本运算。
3.树
树型结构是一种非线性结构,树tree是是由一个或多个结点组成的有限集合。
树有跟结点root(树的根结点没有前驱结点,除根结点之外的所有结点有且只有一个前驱结点),根的子树subtree。树的递归:一棵非空树是由若干子树构成的,而子树又可由若干更小的子树构成。
相关名词:
结点的度:一个结点拥有的子树数目。
树的度:是指该树中结点的最大度数。
叶子结点(Leaf)或终端结点:度为零的结点。
分支结点或非终端结点:度不为零的结点。
孩子结点、双亲结点、兄弟结点、结点的层数(Level)、 树的高度、有序树(二叉树就是有序树)
4.二叉树
二叉树:由一个根结点及两棵互不相交的、分别称作这个根的左子树和右子树的二叉树组成。
满二叉树、完全二叉树;
二叉树的链式存储结构主要是通过二叉链表来存储的。二叉链表的每个结点有一个数据域和两个指针域,一个指针指向左孩子,另一个指针指向右孩子。

struct tagBTNODE
{int data; /* 数据域 */struct tagBTNODE *lchild; /* 左指针域(左孩子) */struct tagBTNODE *rchild; /* 左指针域(右孩子)*/
};二叉树的遍历:
按某条搜索路径访问树中的每一个结点,使得每一个结点均被访问一次并且仅被访问一次。
主要是利用递归操作反复调用自己来实现遍历:
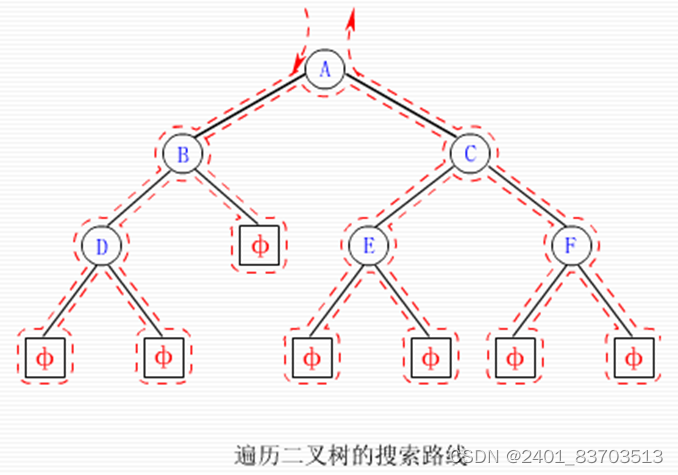
从根结点出发,逆时针沿着二叉树外缘移动,对每个结点均途径三次,最后回到根结点。
①先根遍历(NLR):根左右
如果二叉树为空,则空操作。否则依次执行以下三个操作:
1>. 访问跟结点
2>. 先根遍历左子树
3>. 先根遍历右子树
算法实现如下:
void PreOrder(struct tagBTNODE *root)
{if(root != NULL){ printf("%d", root ->data); PreOrder(root ->lchild);PreOrder(root ->rchild);}
}遍历结果如下:A B D C E F
②中根遍历(LNR):左根右
如果二叉树为空,则空操作。否则依次执行以下三个操作:
1>. 中根遍历左子树
2>. 访问根节点
3>. 中根遍历右子树
算法实现如下:
void InOrder(struct tagBTNODE *root)
{if(root != NULL){InOrder(root ->lchild);printf("%d", root ->data);InOrder(root ->rchild);}
}遍历结果如下:D B A E C F
③后根遍历(LRN):左右根
如果二叉树为空,则空操作。否则依次执行以下三个操作:
1>. 后跟遍历左子树
2>. 后根遍历右子树
3>. 访问根节点
算法实现如下:
void PostOrder(struct tagBTNODE *root)
{if(root != NULL){PostOrder(root ->lchild);PostOrder(root ->rchild);printf("%d", root ->data);}
}遍历结果如下:D B E F C A
三种方式都是利用函数的递归操作进行遍历,根据读取的结点顺序不同,读到的数据顺序也有所不同,在分析时可以利用函数递归知识点里面的画图进行分析。
这篇关于栈、队列、树——知识简单概括的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








