本文主要是介绍关于时频分析的一些事-答知乎问(一),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
从信号的时频谱图中可以提取什么特征?
基于时频谱图的特征一般包括能量特征、时域和频域拓展特征以及时频内禀特征。
基于时频图的能量特征
基于时频图的特征中,能量特征是最简单的一种,通过分析时频谱图中的能量分布特性而获取信号的时频信息,包括某个特定频带的能量、总能量和时频图沿时间轴或频率轴压缩后的统计特征,如下:
(1)特定频带能量 :特定频带能量是指时频图中一行或几行系数之和。
(2)总能量:总能量即整个时频图的系数之和。
(3)时频图沿时间轴或频率轴压缩后的统计特征 。
时频图是一个二维矩阵,把其中各列系数分别求和便得到时频能量随时间的分布;把各行系数分别求和,便得到时频能量随频率的分布。
频域拓展特征
常用的频域特征包括谱通量、谱熵和谱平坦度,然而这些特征不考虑非平稳信号的时变特性。当两个不同信号具有相似的频谱时,频域特征无法对它们进行区分。比如谱平坦度主要用于区分窄带信号和宽带信号,但它不能区分两个具有不同时频特性的宽带信号。 这一问题可通过将频域特征拓展到时频域来解决。
(1)谱通量
谱通量主要用于测量信号的频谱随时间的变化率,将其拓展到时频域之后, 可同时测量信号的时频谱随时间和频率的变化率。
(2)谱熵
谱熵测量频域中信号能量分布的随机性,熵值越大表明信号的随机性越大或者信号在频域中分布均匀,熵值越小表明信号的随机性越小或者能量在频域中分布集中。
(3)谱平坦度
谱平坦度测量信号在频域中能量分布的均匀性,平坦度大说明信号是宽带的,平坦度小说明信号是窄带的,拓展后的谱平坦度测量信号在时频域中能量分布的均匀性。
基于时频图的内禀特征
有一些特征本质上属于时频特征,它们在时域和频域无法进行定义,下面给出基于时频图的内禀特征。
基于奇异值分解的特征
瞬时频率均值
瞬时频率偏差
时频集中度
集合经验模态分解EEMD如何做有效改进?
可以结合统计学上的四分位差方法。
四分位差反映了中间50%数据的离散程度,其定义为上四分位数(Q3,即位于 75%)和下四分位数(Q1,即位于 25%)的差,值越大,反应数据集的离散程度越大,也就是数据分布的越不均匀,而且四分位差不受个别数据极值的影响,避免了统计数据因个别异常点导致无法反应大部分数据特点的缺点。
EEMD中加入白噪声的根本目的在于使信号极大(极小)值点的分布更加均匀, 波动程度尽可能小。四分位差可以表征数据均匀性的度量,四分位差越大,表示数据的不均匀性,也就是波动程度越大。因此可以以四分位差作为特征量,衡量极值点分布的均匀性,通过加入不同幅值系数的白噪声,计算极值点序列间距的四分位差,选择相对四分位差最小时的白噪声幅值系数作为最优参数,根据选取的最优白噪声幅值系数,按照给定的分解误差,计算出相应的聚合次数,达到根据实际分解信号自适应的优化参数的目的。
谱重排变换和同步压缩变换的区别是什么?
谱重排方法能够得到非常高的时频分辨率,但是同样也存在一个问题,不能重构原始信号,2011 年 Daubechies 提出了一种基于相位的高分辨率时频分析方法—同步压缩小波变换,该方法也是一种谱重排的方法,能使非平稳非线性信号在时频域高度聚焦,与传统谱重排不同的是,同步压缩小波变换能够重构原始信号。
谱重排是在谱图等二次型时频分布的基础上重新排列时间-频率坐标系,它对时频谱上的点沿时间和频率两个方向都做了移动,而同步压缩变换是在短时傅里叶变换和小波变换等线性时频分布基础上进行的,只对频率进行重排,没有考虑时间,如下图所示。
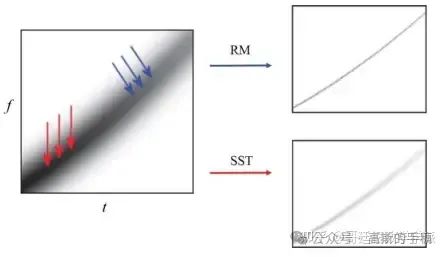
蓝色箭头为谱重排(RM)的能量重排方式,红色箭头为同步压缩变换的能量重排方式。所以谱重排不能重构信号,而同步压缩变换可以。
以一个模拟信号为例,分别做 Gabor变换,小波变换,同步压缩Gabor变换和同步压缩小波变换,这个信号在时间 0-0.35s之间频率为10Hz,0.35s-0.65s之间频率为20Hz,0.65s-1s之间频率为 30Hz。Gabor 变换(图a)具有恒定的时频分辨率,因此对于不同的频率成分,其时频展布是相同的,小波变换(图b)在高频端具有高时间分辨率, 但是频率分辨能力较差,通过同步压缩小波变换(图d),发散的能量得到了很好的聚焦,与同步压缩 Gabor 变换得到的结果(图c)相似,都具有非常高的时频分辨率。

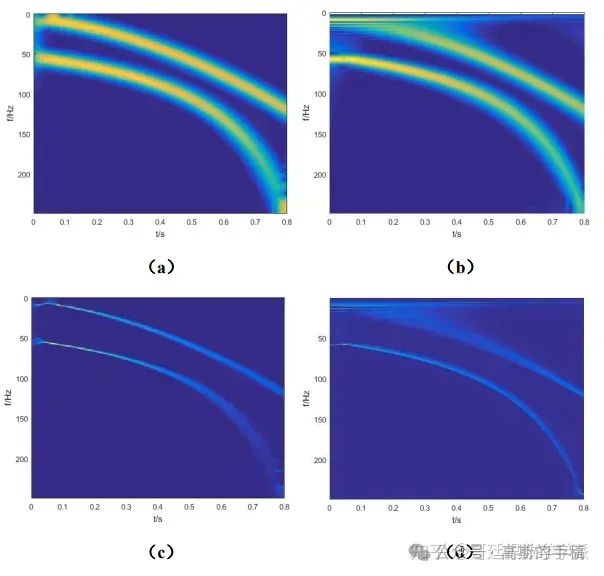
同步压缩变换只在频率方向上进行压缩,因此对于平稳的信号可以得到极高的时频分辨率,但是当信号变化比较剧烈时,时频分辨能力会有所下降。对一个频率变化比较剧烈的信号 ( ):
![]()
分别采用不同的时频分析方法得到的时频谱。Gabor 变换(图a)窗函数固定,所以高频端时间分辨率不足,导致同步压缩 Gabor 变换(图c)高频分辨率不如同步压缩小波变换(图d),小波变 换(图b)在低频端时间分辨率较差,同步压缩小波变换也存在这一问题。
魏格纳分布的交叉项抑制方法主要有哪些?
魏格纳分布属于二次型时频分布,不受Heisenberg不确定性原理的制约,因此具有非常高的时频分辨能力。通过对几种典型信号做魏格纳时频分析可以知道,对于单分量信号,其魏格纳分布只在该信号频率处有脉冲值,因此魏格纳分布具有极高的时频分辨能力,可以精确的展现原始信号的时频分布。但是当输入信号包含两个或者两个以上分量时,魏格纳分布就会存在交叉项的干扰,导致其在实际应用中受到了限制。针对这一问题,可以从不同的角度对其进行了改进,主要概括为三类:
(1)核函数方法
这类方法是对核函数加上制约条件,比如最为熟悉的伪魏格纳分布(PWVD), 平滑伪魏格纳分布(SPWVD)等。除此之外,还有很多方法,包括自适应核函数法,都属于改变核函数抑制交叉项的类型。
(2)信号分解法
这类交叉项抑制方法的出发点是将信号分解成一系列单分量信号,然后对各个分量的信号分别做魏格纳分布,最后线性相加,从而避免了多分量引起的交叉项问题。信号分解的方式有基于经验模态分解的,基于小波包变换的,以及基于频率域“CLEAN”等。
(3)多谱图叠加法
多谱图叠加法的基本思想是利用多种不同时频谱图叠加,通过阈值选取,确定魏格纳分布的支撑区间,然后用该区间函数与魏格纳分布相乘,得到新的时频分析结果。 Gabor-Wigner 变换就是其中一种,以 Gabor 变换作为一种滤波工具,去除魏格纳分布的交叉项。
以上几种交叉项抑制方法各具优势,但也存在一些问题,核函数方法是在时频域加了一个低通滤波窗,抑制交叉项的同时也会降低时频分辨率;对于信号分解法,如何选择分解方式才能得到正确的分量是需要进一步研究的问题;而多谱图叠加法对于阈值选取和支撑区间的选择要求也较高,不合适的处理可能会导致弱信号无法提取。
S 变换与 WVD 之间的关系是什么?
如果一个窗函数是高斯调制的,即 :
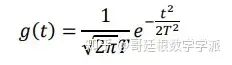
则该窗函数的 WVD 为:

此时,S 变换与 WVD 分布之间的关系为:
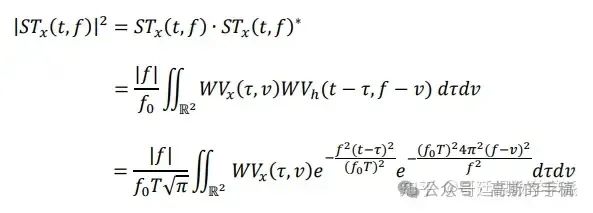
S变换没有交叉项,而 WVD具有较高的时频分辨率,如果将二者结合,既可以避免交叉项问题,又可以提高时频分辨能力。比如可以利用反褶积短时傅里叶谱提高时频分辨率,利用短时傅里叶变换和 WVD之间的关系,得到了比较好的时频聚焦结果。
小波基的构造方法有哪些?
构造小波基的方法多种多样,有构造滤波器法、基于已知小波滤波器系数和完美重构条件的提升算法、根据实际分析需要改进已知函数法、综合已有小波基法和基于机器学习/深度学习的数据驱动的小波构造法等,重点说一下后面3种。
改进已有函数法
在实际应用中,往往需要根据不同的分析目的构造具有不同特性的小波基。通过对已知函数进行改进,构造出的小波基可保留原函数的良好性质,并可根据不同的处理需要对函数的某些特性进行改进。这种小波基构造方法比较简单,且能得到较好的应用效果。Morlet小波是最常用到的复小波,它的函数表达式较简单,且不同的参数具有不同的特性。对Morlet小波进行改进,可得到适用于爆破震动信号分析的复小波和在提取信号特征中具有良好效果的小波基;脉冲冲击作用于二阶弱阻尼振动系统的响应函数具有指数衰减特性,将其稍作调整作为小波基进行应用,可根据不同的冲击条件和振动系统得到不同的小波基,能避免通常情况下需选择不同小波基的繁琐过程。
综合小波函数法
已知的几类经典小波基具有不同的时间频率特性,在信号分析中有各自独特的优势。如Morlet小波在时、频域内均具有良好的局部性,适用于复数信号的分解和时频分析;Gauss小波具有指数衰减特征,在信号和图像的边缘提取中具有良好的应用效果。通过综合几种已知小波基构造出的小波函数可同时具有这几种小波基的优点,并能补充各自的不足,在信号处理中能获得比单个小波基更好的分析效果,应用范围更广。将多个中心频率不同的Morlet小波进行组合得到的小波函数,具有滤波效果好、频率分辨能力强的特点,且能直接锁定信号特征所在频段,从而减少小波变换的计算量;将具有良好滤波性但衰减较慢的Shannon函数和衰减快但低通滤波效果较差的Gauss函数进行结合,可构造出不仅滤波效果好且衰减迅速的小波基;将具有良好光滑性的小波构造成小波库,能取得比单小波更好的信号去噪效果。
利用机器学习模型设计正交小波滤波器
小波变换是一种特殊类型的数学变换,通俗来说,是用有限波的平移和缩放表示信号,就其应用而言,离散小波变换DWT常用于信号编码(典型的JPEG2000格式),而连续小波变换一般用于信号分析。小波的缺点之一是必须事先选择要使用的母小波,例如轴承故障检测中经常使用的Morlet小波,适用于地震信号处理的Ricker小波,适用模态分析的Laplace小波等等,这些一定程度上限制了小波的应用范围。
相关参考见知乎上的如下文章:
形象易懂讲解算法I——小波变换 - 咚懂咚懂咚的文章 - 知乎 https://zhuanlan.zhihu.com/p/22450818
因此,有这样一种想法,即开发一种机器学习或深度学习模型,该模型能够在给定信号的情况下找到正交小波的滤波器 h 和 g,找到的这些滤波器应该足够“好”,以便在对信号应用小波变换时能保留最多的信息。总体思路是建立一种自编码器,其参数是滤波器 h 和 g,对信号X进行小波变换(滤波器 h 和 g), 逆变换反过来。将损失函数通过梯度下降算法迭代优化 h 和 g 的系数, 然后使用新的系数对信号 X 重复第一步的过程。当满足某些停止条件时,过程结束。其实也比较容易理解,本质就是梯度下降算法迭代改进滤波器 h 和 g的系数。
可以参考
利用机器学习模型设计正交小波滤波器 - 哥廷根数学学派的文章 - 知乎 https://zhuanlan.zhihu.com/p/53
知乎学术咨询:
哥廷根数学学派 - 知乎
工学博士,担任《Mechanical System and Signal Processing》等期刊审稿专家,擅长领域:现代信号处理,机器学习,深度学习,数字孪生,时间序列分析,设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。
这篇关于关于时频分析的一些事-答知乎问(一)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





