DP算法的精髓是什么？

2024-04-14 13:20

文章标签 算法 dp 精髓

本文主要是介绍DP算法的精髓是什么？，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

概述

DP(动态规划)通过将原问题拆分成一系列子问题，并通过对子问题求解。所以，也可以把DP算法定义为“多阶段决策最优解模型”（决策树）

同时该模型也具有以下明显特征：

问题的最优解包含子问题的最优解。反过来说的是，可以通过子问题的最优解，推导出问题的最优解
可以理解为，后面阶段的状态可以通过前面阶段的状态推导出来

无后效性(两层含义)

第一层含义，在推导后面阶段的状态的时候，只关心前面阶段的状态值，不关心这个状态是怎么一步一步推导出来的
第二层含义，某阶段状态一旦确定，就不受之后阶段决策影响
不同的决策序列，到达某个相同的阶段时，可能会产生重复的状态

案例 : 找零钱

给定 3 种不同面值的硬币，分别记为 {1,3,5}，同时还有一个总金额 9，求出最少需要几枚硬币凑出这个金额？

回溯图
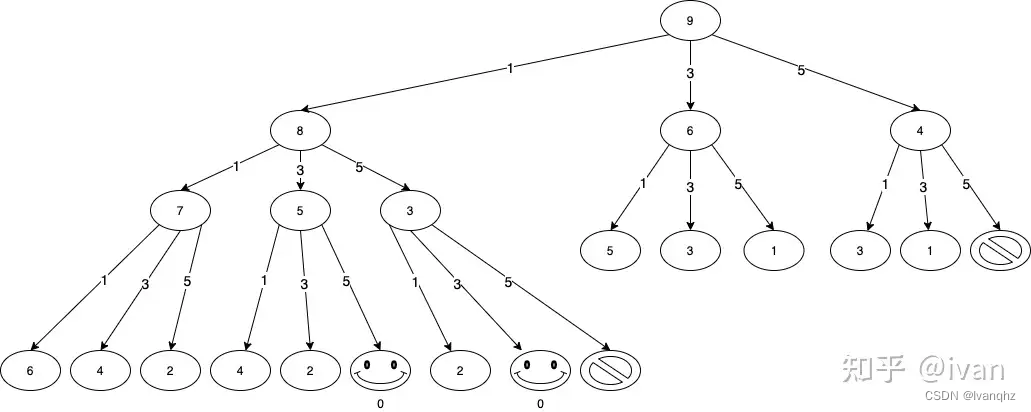
在这里插入图片描述
通过上述回溯图，把整个找零钱的过程，拆分成各个子节点，每个子节点再根据3种不同的硬币进行决策，直到完成整个决策过程

同时确定了初始状态和边界条件，只有3枚硬币的时候，就会只有3种分配方法。通过这个回溯树也可以看到在某个阶段的时候，会出现重复的决策结果

通过回溯树可知金额 9，只能从金额 9 - 1 ＝ 8 和 9 - 3 ＝ 6、9 - 5 = 4 递推过来。用通式表达就是金额只能由金额 money - coin（ coin 为给定硬币中的任一面值）推导出来

整个过程中，只有金额才是变化的量，因此我们可以用一维数组来作为备忘录假设 DP(money) 表示凑出金额9需要的最少硬币个数，那么，DP(money) 可以表示为:

DP(money) = min(1 + DP(money - coin))

动态规划代码:

#include <stdio.h>
#include <vector>
#include <limits.h>
#include <iostream>using namespace std;
#define MIN(a, b) (a) > (b) ? (b) : (a)int minCoins(int money, const std::vector<int>& coins, std::vector<int>& dp) {int coinsLength = coins.size();for(int i = 1; i < money + 1; i++) {for(int j = 0; j < coinsLength; j++) {int v = coins[j];if (i < v) { continue; }dp[i] = MIN(dp[i], dp[i - v] + 1);}}return dp[money];
}int main() {int coinsArr[] = {1, 3, 5};std::vector<int> coins(coinsArr, coinsArr + sizeof(coinsArr) / sizeof(coinsArr[0]));int money = 9;std::vector<int> dp(money + 1, money + 1); // 备忘录，值初始化为k+1dp[0] = 0;int minCount = minCoins(money, coins, dp);printf(" minCount = %d\n", minCount);return 0;
}

状态转移表变化: