吴恩达机器学习-实践实验室：协同过滤推荐系统（Collaborative Filtering Recommender Systems）

本文主要是介绍吴恩达机器学习-实践实验室：协同过滤推荐系统（Collaborative Filtering Recommender Systems），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在本练习中，您将实现协作过滤，以构建电影推荐系统。

软件包
我们将使用现在熟悉的NumPy和Tensorflow软件包。

import numpy as np
import tensorflow as tf
from tensorflow import keras
from recsys_utils import *

1-概念

下面这段文字描述了一些符号和符号的含义，这些符号通常在协同过滤推荐系统中使用。

• 𝑟(𝑖,𝑗): 标量，如果用户 j 对游戏 i 进行了评分，𝑟(𝑖,𝑗) = 1，否则为 0。
• 𝑦(𝑖,𝑗): 标量，表示用户 j 对游戏 i 给出的评分（仅当 r(i,j) = 1 时定义）。
• 𝐰(𝑗): 向量，表示用户 j 的参数。
• 𝑏(𝑗): 标量，表示用户 j 的参数。
• 𝐱(𝑖): 向量，表示游戏 i 的特征评分。
• 𝑛𝑢: 用户的数量。
• 𝑛𝑚: 游戏的数量。
• 𝑛: 特征的数量。
• 𝐗: 向量 𝐱(𝑖) 的矩阵，表示游戏特征。
• 𝐖: 向量 𝐰(𝑗) 的矩阵，表示用户参数。
• 𝐛: 偏置参数向量 𝑏(𝑗)。
• 𝐑: 元素为 𝑟(𝑖,𝑗) 的矩阵，表示评分矩阵。

这些符号用于描述协同过滤推荐系统中的用户、游戏、评分和参数。通过使用这些符号，可以方便地表示和操作相关的变量和矩阵。

2-推荐系统

在这个实验室中，您将实现协作过滤学习算法，并将其应用于电影评级数据集。协同过滤推荐系统的目标是生成两个向量：对于每个用户，一个体现用户电影品味的“参数向量”。对于每部电影，都有一个相同大小的特征向量，它体现了对电影的一些描述。两个向量的点积加上偏差项应该会产生用户可能对该电影的评分的估计。
下图详细说明了如何学习这些向量。

下面这段文字描述了一个协同过滤推荐系统中的训练数据和参数学习过程。

• 𝑌 是一个矩阵，包含了电影的评分。评分的范围是从0.5到5，以0.5为步长。如果电影没有被评分，则相应的值为0。
• 𝑅 是一个矩阵，其中1表示电影已被评分，0表示电影未被评分。电影在行中，用户在列中。
• 每个用户都有一个参数向量 𝑤𝑢𝑠𝑒𝑟 和一个偏置值。
• 每个电影都有一个特征向量 𝑥𝑚𝑜𝑣𝑖𝑒。
• 这些向量是通过使用现有的用户/电影评分作为训练数据同时进行学习的。上面给出了一个训练示例：𝐰(1)⋅𝐱(1)+𝑏(1)=4。
• 值得注意的是，特征向量 𝑥𝑚𝑜𝑣𝑖𝑒 必须适应所有的用户，而用户向量 𝑤𝑢𝑠𝑒𝑟 必须适应所有的电影。这是这种方法名称的来源——所有的用户共同生成评分集。

简单来说，这段文字描述了在协同过滤推荐系统中使用现有的评分数据作为训练样本，通过学习用户参数向量和电影特征向量来预测缺失的评分。用户和电影的参数向量通过协同合作进行学习，以生成整个评分集。这个过程旨在捕捉用户和电影之间的相关性和偏好，从而提供个性化的推荐。

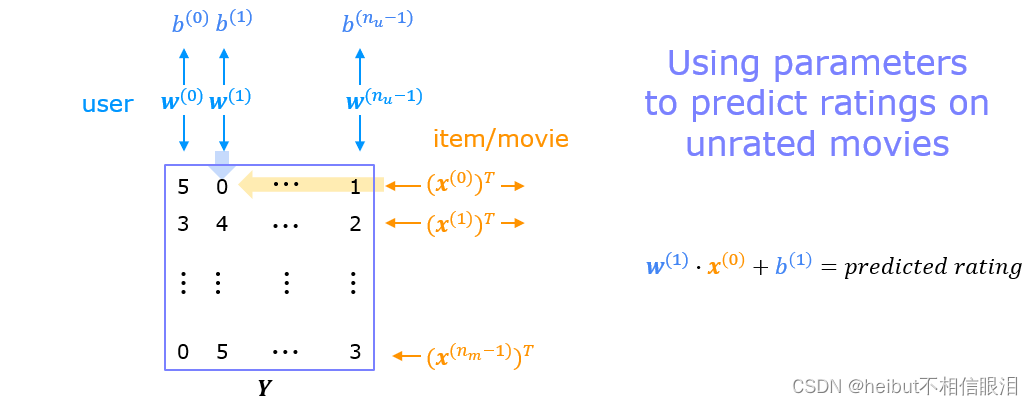
一旦学习了特征向量和参数，它们就可以用来预测用户对未分级电影的评分。如上图所示。该等式是预测用户一对电影零的评分的示例。
在本练习中，您将实现计算协作过滤目标函数的函数cofiCostFunc。实现目标函数后，您将使用TensorFlow自定义训练循环来学习协同过滤的参数。第一步是详细说明实验室中使用的数据集和数据结构。

3-电影评分数据集

这段文字提供了关于MovieLens数据集和在练习中使用的矩阵的信息。以下是关键点的解释：

1. MovieLens数据集：该练习使用的数据集源自MovieLens的"ml-latest-small"数据集。原始数据集包含了600个用户对9000部电影的评分。

2. 数据集尺寸缩减：为了侧重于2000年以后的电影，数据集的大小进行了缩减。缩减后的数据集包含了0.5到5之间以0.5为步长的评分。

3. 数据集维度：缩减后的数据集包含了443个用户（𝑛𝑢）和4778部电影（𝑛𝑚）。

4. 矩阵𝑌：矩阵𝑌是一个𝑛𝑚×𝑛𝑢的矩阵，用于存储评分𝑦(𝑖,𝑗)。每个元素𝑦(𝑖,𝑗)表示用户𝑗对电影𝑖的评分。

5. 矩阵𝑅：矩阵𝑅是一个二值指示矩阵，与𝑌具有相同的维度。元素𝑅(𝑖,𝑗)等于1表示用户𝑗对电影𝑖进行了评分，等于0表示没有评分。该矩阵有助于确定𝑌中哪些条目是有效的评分。

在这部分练习中，您还将使用矩阵𝐗、𝐖和𝐛：

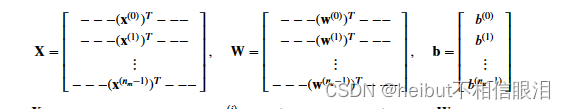
下面这段文字解释了矩阵𝐗、𝐖和向量𝐛的含义和结构。以下是关键点的解释：

1. 𝐗矩阵：𝐗矩阵的第𝑖行对应于第𝑖部电影的特征向量𝑥(𝑖)。𝑥(𝑖)是一个𝑛维向量，表示第𝑖部电影的特征。在这个练习中，𝑛的取值为10，因此𝑥(𝑖)是一个包含10个元素的向量。𝐗是一个𝑛𝑚×10的矩阵，其中𝑛𝑚是电影的数量。

2. 𝐖矩阵：𝐖矩阵的第𝑗行对应于第𝑗个用户的参数向量𝐰(𝑗)。𝐰(𝑗)是一个𝑛维向量，表示第𝑗个用户的参数。与𝐗类似，𝐰(𝑗)也包含10个元素。𝐖是一个𝑛𝑢×10的矩阵，其中𝑛𝑢是用户的数量。

3. 𝐛向量：𝐛是一个预先计算的值向量。在这个练习中，它将被用于开发成本模型。

在这段文字中，提到了𝑌和𝑅矩阵将与电影数据集一起加载。同时，𝐗、𝐖和𝐛也会被加载，并且这些预先计算的值将在后面的实验中进行学习。

#Load data
X, W, b, num_movies, num_features, num_users = load_precalc_params_small()
Y, R = load_ratings_small()print("Y", Y.shape, "R", R.shape)
print("X", X.shape)
print("W", W.shape)
print("b", b.shape)
print("num_features", num_features)
print("num_movies",   num_movies)
print("num_users",    num_users)

Y (4778, 443) R (4778, 443)
X (4778, 10)
W (443, 10)
b (1, 443)
num_features 10
num_movies 4778
num_users 443

#  From the matrix, we can compute statistics like average rating.
tsmean =  np.mean(Y[0, R[0, :].astype(bool)])
print(f"Average rating for movie 1 : {tsmean:0.3f} / 5" )

Average rating for movie 1 : 3.400 / 5

这段代码计算了电影1的平均评分。让我逐步解释代码的含义：

1. Y[0, R[0, :].astype(bool)]: 这部分代码使用索引操作符[]来获取矩阵Y中的一部分数据。Y[0, :]表示获取Y矩阵的第1行（电影1的评分数据）。R[0, :]表示获取R矩阵的第1行（与电影1相关的评分指示器）。.astype(bool)将R矩阵的元素转换为布尔类型，将非零值转换为True，零值转换为False。这样做是为了过滤掉没有评分的条目。

2. np.mean(Y[0, R[0, :].astype(bool)]): 这部分代码使用NumPy库的mean函数计算指定数据的平均值。在这里，我们计算了电影1的评分数据的平均值。即对电影1所有有评分的数据进行求平均。

3. f"Average rating for movie 1 : {tsmean:0.3f} / 5": 这部分代码使用了f-string格式化字符串的功能，将计算得到的平均评分tsmean插入到字符串中。:0.3f表示将tsmean格式化为小数点后三位的浮点数。最终的输出是一个字符串，显示电影1的平均评分。

因此，这段代码的作用是计算电影1的平均评分，并将结果打印输出。

“/ 5” 是表示评分的范围。在这个上下文中，评分的范围是从0.5到5，以0.5为步长，总共有10个等级。所以"/ 5" 的含义是将评分结果显示为在5分制下的评分等级

4-协作过滤学习算法

现在，您将开始实现协作过滤学习算法。您将从实现目标函数开始。

1. 参数向量：协同过滤算法考虑了一组𝑛维参数向量，包括电影的参数向量𝐱(0),…,𝐱(𝑛𝑚−1)，用户的参数向量𝐰(0),…,𝐰(𝑛𝑢−1)，以及偏置向量𝑏(0),…,𝑏(𝑛𝑢−1)。这些参数向量用于预测用户𝑗对电影𝑖的评分𝑦(𝑖,𝑗)。

2. 预测评分：模型通过计算内积𝐰(𝑗)⋅𝐱(𝑖)加上偏置𝑏(𝑖)来预测电影𝑖由用户𝑗的评分𝑦(𝑖,𝑗)。这个预测值表示为𝑦(𝑖,𝑗)=𝐰(𝑗)⋅𝐱(𝑖)+𝑏(𝑖)。

3. 目标：给定一个由一些用户对一些电影产生的评分数据集，目标是学习参数向量𝐱(0),…,𝐱(𝑛𝑚−1),𝐰(0),…,𝐰(𝑛𝑢−1)和𝑏(0),…,𝑏(𝑛𝑢−1)，以使其最佳拟合（最小化平方误差）。

这段文字提到了你需要完成的cofiCostFunc代码，用于计算协同过滤的成本函数。在该函数中，你将计算协同过滤的成本函数，用于衡量预测评分与实际评分之间的差异。

4.1协同过滤成本函数

协同过滤成本函数由下式给出

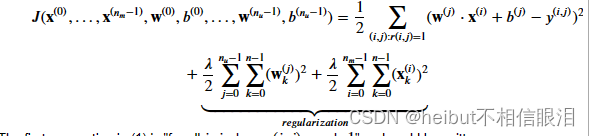
（1）中的第一个总和是“对于所有𝑖, 𝑗。𝑟(𝑖,𝑗)=1并且可以写成：

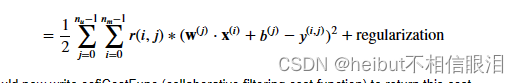
您现在应该编写cofiCostFunc（协作过滤成本函数）来返回此成本。

练习1
循环实施：
首先使用for循环实现成本函数。考虑分两步开发成本函数。首先，在没有正则化的情况下开发成本函数。下面提供了一个不包括正则化的测试用例来测试您的实现。一旦这起作用，添加正则化并运行包括正则化的测试。请注意：当计算成本函数时，只有当𝑅(𝑖,𝑗)等于1时，才应该累积用户𝑗对电影𝑖的评分差异。也就是说，只有在用户对电影进行了评分的情况下，才会考虑该评分对成本函数的贡献。
正确答案：

#wuenda
# GRADED FUNCTION: cofi_cost_func
# UNQ_C1def cofi_cost_func(X, W, b, Y, R, lambda_):"""Returns the cost for the content-based filteringArgs:X (ndarray (num_movies,num_features)): matrix of item featuresW (ndarray (num_users,num_features)) : matrix of user parametersb (ndarray (1, num_users)            : vector of user parametersY (ndarray (num_movies,num_users)    : matrix of user ratings of moviesR (ndarray (num_movies,num_users)    : matrix, where R(i, j) = 1 if the i-th movies was rated by the j-th userlambda_ (float): regularization parameterReturns:J (float) : Cost"""nm, nu = Y.shapen=W.shape[1]J = 0### START CODE HERE ###  for j in range(nu):w = W[j,:]b_j = b[0,j]for i in range(nm):x = X[i,:]y = Y[i,j]r = R[i,j]J += np.square(r * (np.dot(w,x) + b_j - y ) )J = J/2### END CODE HERE ### J += lambda_/2* (np.sum(np.square(W)) + np.sum(np.square(X)))return J

我的答案：

	J = 0regularization_w=0regularization_x=0### START CODE HERE ###  for j in range(nu):for i in range(nm):J=J+R[i][j]*(np.dot(W[j],X[i])+b[0][j]-Y[i][j])**2J=J/2if lambda_:for j in range(nu):for k in range(n):regularization_w=regularization_w+W[j][k]**2for i in range(nm):for k in range(n):regularization_x=regularization_x+X[i][k]**2regularization=lambda_/2*(regularization_w+regularization_x)   J=J+ regularization      ### END CODE HERE ### 

poe答案：

    J = 0for j in range(nu):for i in range(nm):if R[i][j] == 1:J += R[i][j] * (np.dot(W[j], X[i]) + b[0][j] - Y[i][j]) ** 2J /= 2if lambda_:regularization_w = np.sum(W**2)regularization_x = np.sum(X**2)regularization = lambda_ / 2 * (regularization_w + regularization_x)J += regularization

检验：

# Public tests
from public_tests import *
test_cofi_cost_func(cofi_cost_func)

All tests passed!

测试前4个人对前5个电影实际打分喝预测之前的误差：

# Reduce the data set size so that this runs faster
num_users_r = 4
num_movies_r = 5 
num_features_r = 3X_r = X[:num_movies_r, :num_features_r]
W_r = W[:num_users_r,  :num_features_r]
b_r = b[0, :num_users_r].reshape(1,-1)
Y_r = Y[:num_movies_r, :num_users_r]
R_r = R[:num_movies_r, :num_users_r]# Evaluate cost function
J = cofi_cost_func(X_r, W_r, b_r, Y_r, R_r, 0);
print(f"Cost: {J:0.2f}")

Cost: 13.67

Expected Output (lambda = 0):
13.67

加入正则化之后对比：

# Evaluate cost function with regularization 
J = cofi_cost_func(X_r, W_r, b_r, Y_r, R_r, 1.5);
print(f"Cost (with regularization): {J:0.2f}")

Cost (with regularization): 28.09

Expected Output:

28.09

矢量化实现
创建一个矢量化实现来计算𝐽是很重要的，因为它将在优化过程中被多次调用。所使用的线性代数不是本系列的重点，因此提供了实现。如果您是线性代数方面的专家，可以随意创建自己的版本，而无需引用下面的代码。

运行下面的代码并验证它是否产生与未向量化版本相同的结果。

def cofi_cost_func_v(X, W, b, Y, R, lambda_):"""Returns the cost for the content-based filteringVectorized for speed. Uses tensorflow operations to be compatible with custom training loop.Args:X (ndarray (num_movies,num_features)): matrix of item featuresW (ndarray (num_users,num_features)) : matrix of user parametersb (ndarray (1, num_users)            : vector of user parametersY (ndarray (num_movies,num_users)    : matrix of user ratings of moviesR (ndarray (num_movies,num_users)    : matrix, where R(i, j) = 1 if the i-th movies was rated by the j-th userlambda_ (float): regularization parameterReturns:J (float) : Cost"""j = (tf.linalg.matmul(X, tf.transpose(W)) + b - Y)*RJ = 0.5 * tf.reduce_sum(j**2) + (lambda_/2) * (tf.reduce_sum(X**2) + tf.reduce_sum(W**2))return J

# Evaluate cost function
J = cofi_cost_func_v(X_r, W_r, b_r, Y_r, R_r, 0);
print(f"Cost: {J:0.2f}")# Evaluate cost function with regularization 
J = cofi_cost_func_v(X_r, W_r, b_r, Y_r, R_r, 1.5);
print(f"Cost (with regularization): {J:0.2f}")

Cost: 13.67
Cost (with regularization): 28.09

Expected Output:
Cost: 13.67
Cost (with regularization): 28.09

5-学习电影推荐

在完成协同过滤成本函数的实现后，您可以开始训练算法，为自己推荐电影。
在下面的单元格中，您可以输入自己的电影选择。然后算法将为您提供建议！我们已经根据自己的喜好填写了一些值，但在您对我们的选择进行处理后，您应该根据自己的口味进行更改。数据集中所有电影的列表在文件电影列表中。

movieList, movieList_df = load_Movie_List_pd()my_ratings = np.zeros(num_movies)          #  Initialize my ratings# Check the file small_movie_list.csv for id of each movie in our dataset
# For example, Toy Story 3 (2010) has ID 2700, so to rate it "5", you can set
my_ratings[2700] = 5 #Or suppose you did not enjoy Persuasion (2007), you can set
my_ratings[2609] = 2;# We have selected a few movies we liked / did not like and the ratings we
# gave are as follows:
my_ratings[929]  = 5   # Lord of the Rings: The Return of the King, The
my_ratings[246]  = 5   # Shrek (2001)
my_ratings[2716] = 3   # Inception
my_ratings[1150] = 5   # Incredibles, The (2004)
my_ratings[382]  = 2   # Amelie (Fabuleux destin d'Amélie Poulain, Le)
my_ratings[366]  = 5   # Harry Potter and the Sorcerer's Stone (a.k.a. Harry Potter and the Philosopher's Stone) (2001)
my_ratings[622]  = 5   # Harry Potter and the Chamber of Secrets (2002)
my_ratings[988]  = 3   # Eternal Sunshine of the Spotless Mind (2004)
my_ratings[2925] = 1   # Louis Theroux: Law & Disorder (2008)
my_ratings[2937] = 1   # Nothing to Declare (Rien à déclarer)
my_ratings[793]  = 5   # Pirates of the Caribbean: The Curse of the Black Pearl (2003)
my_rated = [i for i in range(len(my_ratings)) if my_ratings[i] > 0]print('\nNew user ratings:\n')
for i in range(len(my_ratings)):if my_ratings[i] > 0 :print(f'Rated {my_ratings[i]} for  {movieList_df.loc[i,"title"]}');

New user ratings:Rated 5.0 for  Shrek (2001)
Rated 5.0 for  Harry Potter and the Sorcerer's Stone (a.k.a. Harry Potter and the Philosopher's Stone) (2001)
Rated 2.0 for  Amelie (Fabuleux destin d'Amélie Poulain, Le) (2001)
Rated 5.0 for  Harry Potter and the Chamber of Secrets (2002)
Rated 5.0 for  Pirates of the Caribbean: The Curse of the Black Pearl (2003)
Rated 5.0 for  Lord of the Rings: The Return of the King, The (2003)
Rated 3.0 for  Eternal Sunshine of the Spotless Mind (2004)
Rated 5.0 for  Incredibles, The (2004)
Rated 2.0 for  Persuasion (2007)
Rated 5.0 for  Toy Story 3 (2010)
Rated 3.0 for  Inception (2010)
Rated 1.0 for  Louis Theroux: Law & Disorder (2008)
Rated 1.0 for  Nothing to Declare (Rien à déclarer) (2010)

现在，让我们将这些评论添加到𝑌和𝑅并将评级标准化。

# Reload ratings and add new ratings
Y, R = load_ratings_small()
Y    = np.c_[my_ratings, Y]
R    = np.c_[(my_ratings != 0).astype(int), R]# Normalize the Dataset
Ynorm, Ymean = normalizeRatings(Y, R)

让我们准备训练模型。初始化参数并选择Adam优化器。

#  Useful Values
num_movies, num_users = Y.shape
num_features = 100# Set Initial Parameters (W, X), use tf.Variable to track these variables
tf.random.set_seed(1234) # for consistent results
W = tf.Variable(tf.random.normal((num_users,  num_features),dtype=tf.float64),  name='W')
X = tf.Variable(tf.random.normal((num_movies, num_features),dtype=tf.float64),  name='X')
b = tf.Variable(tf.random.normal((1,          num_users),   dtype=tf.float64),  name='b')# Instantiate an optimizer.
optimizer = keras.optimizers.Adam(learning_rate=1e-1)

学习中涉及的操作𝑤, 𝑏和𝑥同时不属于TensorFlow神经网络包中提供的典型“层”。因此，课程2中使用的流：Model、Compile（）、Fit（）、Predict（）不直接适用。相反，我们可以使用自定义的训练循环。

• 回想一下早期实验室的梯度下降步骤。
• 重复直到收敛：
  • 计算前向通过
  • 计算损失相对于参数的导数
  • 使用学习率更新参数，计算出的导数

TensorFlow具有为您计算导数的非凡能力。如下所示。在tf.GradientTape（）部分中，跟踪对Tensorflow Variables的操作。稍后调用tape.gradient（）时，它将返回相对于跟踪变量的损失梯度。然后可以使用优化器将梯度应用于参数。这是对TensorFlow和其他机器学习框架的一个有用功能的非常简短的介绍。进一步的信息可以通过调查感兴趣的框架内的“自定义训练循环”来找到。

iterations = 200
lambda_ = 1
for iter in range(iterations):# Use TensorFlow’s GradientTape# to record the operations used to compute the cost with tf.GradientTape() as tape:# Compute the cost (forward pass included in cost)cost_value = cofi_cost_func_v(X, W, b, Ynorm, R, lambda_)# Use the gradient tape to automatically retrieve# the gradients of the trainable variables with respect to the lossgrads = tape.gradient( cost_value, [X,W,b] )# Run one step of gradient descent by updating# the value of the variables to minimize the loss.optimizer.apply_gradients( zip(grads, [X,W,b]) )# Log periodically.if iter % 20 == 0:print(f"Training loss at iteration {iter}: {cost_value:0.1f}")

Training loss at iteration 0: 2321191.3
Training loss at iteration 20: 136169.3
Training loss at iteration 40: 51863.7
Training loss at iteration 60: 24599.0
Training loss at iteration 80: 13630.6
Training loss at iteration 100: 8487.7
Training loss at iteration 120: 5807.8
Training loss at iteration 140: 4311.6
Training loss at iteration 160: 3435.3
Training loss at iteration 180: 2902.1

6-建议

下面，我们计算所有电影和用户的评分，并显示推荐的电影。这些是基于以上my_ratings[]输入的电影和评分。预测电影的评分𝑖对于用户𝑗，你计算𝐰(𝑗)⋅𝐱(𝑖)+𝑏(𝑗)
这可以使用矩阵乘法对所有评级进行计算。

# Make a prediction using trained weights and biases
p = np.matmul(X.numpy(), np.transpose(W.numpy())) + b.numpy()#restore the mean
pm = p + Ymeanmy_predictions = pm[:,0]# sort predictions
ix = tf.argsort(my_predictions, direction='DESCENDING')for i in range(17):j = ix[i]if j not in my_rated:print(f'Predicting rating {my_predictions[j]:0.2f} for movie {movieList[j]}')print('\n\nOriginal vs Predicted ratings:\n')
for i in range(len(my_ratings)):if my_ratings[i] > 0:print(f'Original {my_ratings[i]}, Predicted {my_predictions[i]:0.2f} for {movieList[i]}')

Predicting rating 4.49 for movie My Sassy Girl (Yeopgijeogin geunyeo) (2001)
Predicting rating 4.48 for movie Martin Lawrence Live: Runteldat (2002)
Predicting rating 4.48 for movie Memento (2000)
Predicting rating 4.47 for movie Delirium (2014)
Predicting rating 4.47 for movie Laggies (2014)
Predicting rating 4.47 for movie One I Love, The (2014)
Predicting rating 4.46 for movie Particle Fever (2013)
Predicting rating 4.45 for movie Eichmann (2007)
Predicting rating 4.45 for movie Battle Royale 2: Requiem (Batoru rowaiaru II: Chinkonka) (2003)
Predicting rating 4.45 for movie Into the Abyss (2011)Original vs Predicted ratings:Original 5.0, Predicted 4.90 for Shrek (2001)
Original 5.0, Predicted 4.84 for Harry Potter and the Sorcerer's Stone (a.k.a. Harry Potter and the Philosopher's Stone) (2001)
Original 2.0, Predicted 2.13 for Amelie (Fabuleux destin d'Amélie Poulain, Le) (2001)
Original 5.0, Predicted 4.88 for Harry Potter and the Chamber of Secrets (2002)
Original 5.0, Predicted 4.87 for Pirates of the Caribbean: The Curse of the Black Pearl (2003)
Original 5.0, Predicted 4.89 for Lord of the Rings: The Return of the King, The (2003)
Original 3.0, Predicted 3.00 for Eternal Sunshine of the Spotless Mind (2004)
Original 5.0, Predicted 4.90 for Incredibles, The (2004)
Original 2.0, Predicted 2.11 for Persuasion (2007)
Original 5.0, Predicted 4.80 for Toy Story 3 (2010)
Original 3.0, Predicted 3.00 for Inception (2010)
Original 1.0, Predicted 1.41 for Louis Theroux: Law & Disorder (2008)
Original 1.0, Predicted 1.26 for Nothing to Declare (Rien à déclarer) (2010)

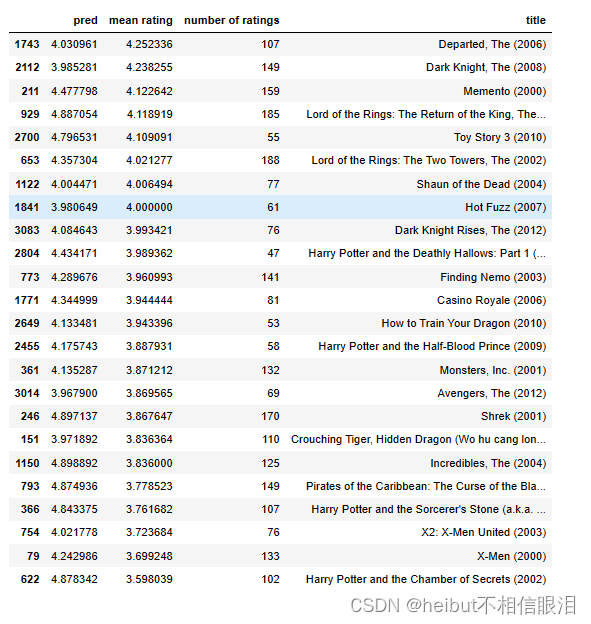
在实践中，可以利用额外的信息来增强我们的预测。上面，前几百部电影的预测收视率范围很小。我们可以通过从那些顶级电影、平均收视率高的电影和收视率超过20的电影中进行选择来扩大上述内容。本节使用Pandas数据框架，该框架具有许多方便的排序功能。

filter=(movieList_df["number of ratings"] > 20)
movieList_df["pred"] = my_predictions
movieList_df = movieList_df.reindex(columns=["pred", "mean rating", "number of ratings", "title"])
movieList_df.loc[ix[:300]].loc[filter].sort_values("mean rating", ascending=False)

7-祝贺

你已经实现了一个有用的推荐系统！

这篇关于吴恩达机器学习-实践实验室：协同过滤推荐系统（Collaborative Filtering Recommender Systems）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---