LeetCode-152. 乘积最大子数组【数组动态规划】

本文主要是介绍LeetCode-152. 乘积最大子数组【数组动态规划】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

LeetCode-152. 乘积最大子数组【数组动态规划】

题目描述：
解题思路一：动态规划五部曲：定推初遍举
解题思路二：因为每一个状态只与前一个状态有关，可以使用「滚动变量」技巧，使用常数个变量完成这道问题。
解题思路三：0

题目描述：

给你一个整数数组 nums ，请你找出数组中乘积最大的非空连续
子数组
（该子数组中至少包含一个数字），并返回该子数组所对应的乘积。

测试用例的答案是一个 32-位整数。

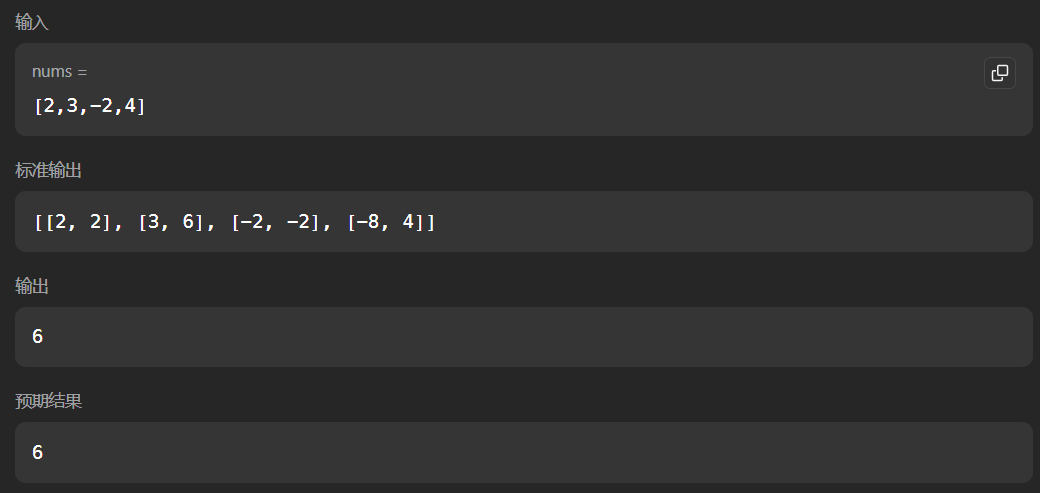
示例 1:

输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:

输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。

提示:

1 <= nums.length <= 2 * 10⁴
-10 <= nums[i] <= 10
nums 的任何前缀或后缀的乘积都保证是一个 32-位整数

解题思路一：动态规划五部曲：定推初遍举

dp定义
以下标 i 结尾的连续子序列的乘积的最大值。
牢记状态的定义，一定以下标 i 结尾，即：乘积数组中 nums[i] 必须被选取。
- 如果 dp[i - 1] 是负数，乘上 nums[i] 还是负数，倒不如另起炉灶。
- 如果 nums[i] 是负数该怎么办呢？dp[i - 1] 是正数的时候，越乘越小，dp[i - 1] 是负数的时候，越乘越大，于是我们可能就需要记录一下负数的那个最小数。

遇到这样的问题，其实就在提示我们状态不够用了。因此，需要在原来的一维 dp 后面新增一个状态。

针对这道题，第 2 维状态只需要两个：

用 0 表示遍历的过程中得到的以 nums[i] 结尾的连续子序列的乘积的最小值；
用 1 表示遍历的过程中得到的以 nums[i] 结尾的连续子序列的乘积的最大值。

当 nums[i] = 0 的时候包含在上面二者之中，无需单独讨论。

状态转移方程写在了参考代码 1 中。即使用二维状态数组同时记录乘积的最大值和最小值，本来写了一堆文字的，后来看太长了，好多废话，直接看代码比较清楚一些。

这里就声明一下状态：

dp[i][1] 表示：以 nums[i] 结尾的连续子序列的乘积的最大值；
dp[i][0] 表示：以 nums[i] 结尾的连续子序列的乘积的最小值。

推导公式

if nums[i] >= 0:dp[i][1] = max(nums[i], dp[i-1][1] * nums[i])dp[i][0] = min(nums[i], dp[i-1][0] * nums[i])else:dp[i][1] = max(nums[i], dp[i-1][0] * nums[i])dp[i][0] = max(nums[i], dp[i-1][1] * nums[i])

初始化

dp = [[0, 0] for _ in range(n)]dp[0][0] = nums[0]dp[0][1] = nums[0]

遍历顺序，显然是从前往后

for i in range(1, n):

举例

class Solution:def maxProduct(self, nums: List[int]) -> int:n = len(nums)if n == 0:return 0dp = [[0, 0] for _ in range(n)]dp[0][0] = nums[0]dp[0][1] = nums[0]for i in range(1, n):if nums[i] >= 0:dp[i][1] = max(nums[i], dp[i-1][1] * nums[i])dp[i][0] = min(nums[i], dp[i-1][0] * nums[i])else:dp[i][1] = max(nums[i], dp[i-1][0] * nums[i])dp[i][0] = min(nums[i], dp[i-1][1] * nums[i])# print(dp)ans = dp[0][1]for i in range(1, n):ans = max(ans, dp[i][1])return ans

时间复杂度：O(n)
空间复杂度：O(n)

解题思路二：因为每一个状态只与前一个状态有关，可以使用「滚动变量」技巧，使用常数个变量完成这道问题。

class Solution:def maxProduct(self, nums: List[int]) -> int:n = len(nums)if n == 0:return 0# dp = [[0, 0] for _ in range(n)]# dp[0][0] = nums[0]# dp[0][1] = nums[0]preMax = nums[0]preMin = nums[0]curMax = preMaxcurMin = preMinans = nums[0]for i in range(1, n):if nums[i] >= 0:curMax = max(nums[i], preMax * nums[i])curMin = min(nums[i], preMin * nums[i])else:curMax = max(nums[i], preMin * nums[i])curMin = min(nums[i], preMax * nums[i])ans = max(ans, curMax)# 滚动变量preMax = curMaxpreMin = curMinreturn ans