【算法一则】做算法学数据结构 - 简化路径

本文主要是介绍【算法一则】做算法学数据结构 - 简化路径 - 【栈】，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

题目

给你一个字符串 path ，表示指向某一文件或目录的 Unix 风格绝对路径（以 ‘/’ 开头），请你将其转化为更加简洁的规范路径。

在 Unix 风格的文件系统中，一个点（.）表示当前目录本身；此外，两个点（…）表示将目录切换到上一级（指向父目录）；两者都可以是复杂相对路径的组成部分。任意多个连续的斜杠（即，‘//’）都被视为单个斜杠 ‘/’ 。对于此问题，任何其他格式的点（例如，‘…’）均被视为文件/目录名称。

请注意，返回的规范路径必须遵循下述格式：

始终以斜杠 ‘/’ 开头。
两个目录名之间必须只有一个斜杠 ‘/’ 。
最后一个目录名（如果存在）不能以 ‘/’ 结尾。
此外，路径仅包含从根目录到目标文件或目录的路径上的目录（即，不含 ‘.’ 或 ‘…’）。
返回简化后得到的规范路径。

示例 1：输入：path = "/home/"
输出："/home"
解释：注意，最后一个目录名后面没有斜杠。 
示例 2：输入：path = "/../"
输出："/"
解释：从根目录向上一级是不可行的，因为根目录是你可以到达的最高级。
示例 3：输入：path = "/home//foo/"
输出："/home/foo"
解释：在规范路径中，多个连续斜杠需要用一个斜杠替换。
示例 4：输入：path = "/a/./b/../../c/"
输出："/c"
提示：1 <= path.length <= 3000
path 由英文字母，数字，'.'，'/' 或 '_' 组成。
path 是一个有效的 Unix 风格绝对路径。

栈

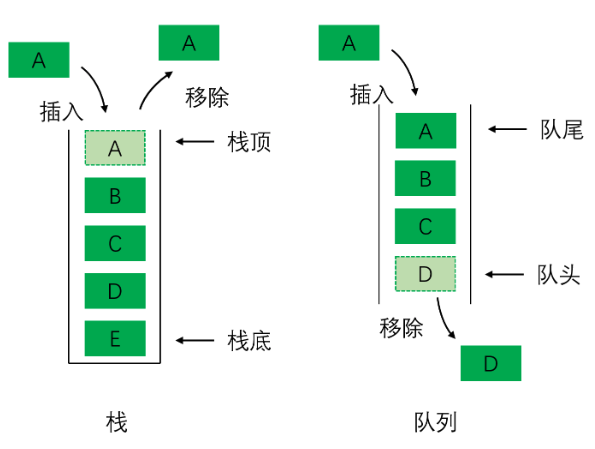
在这里插入图片描述

栈是一种常见的数据结构，它遵循先进后出（LIFO）的原则。栈有两个主要的操作：入栈（push）和出栈（pop）。入栈操作将元素放入栈的顶部，出栈操作将栈顶的元素移除并返回。

以下是一个简单的栈的Java实现示例：

import java.util.ArrayList;
import java.util.EmptyStackException;
import java.util.List;public class Stack<T> {private List<T> stackList;public Stack() {stackList = new ArrayList<>();}public void push(T element) {stackList.add(element);}public T pop() {if (isEmpty()) {throw new EmptyStackException();}int lastIndex = stackList.size() - 1;T element = stackList.get(lastIndex);stackList.remove(lastIndex);return element;}public T peek() {if (isEmpty()) {throw new EmptyStackException();}return stackList.get(stackList.size() - 1);}public boolean isEmpty() {return stackList.isEmpty();}public int size() {return stackList.size();}
}

上述代码中，我们使用一个 List 来存储栈中的元素。push 方法将元素添加到列表的末尾，pop 方法从列表的末尾移除元素并返回它。peek 方法返回栈顶的元素而不移除它。isEmpty 方法用于检查栈是否为空，size 方法返回栈的大小。

使用该栈的示例：

public class Main {public static void main(String[] args) {Stack<Integer> stack = new Stack<>();stack.push(1);stack.push(2);stack.push(3);System.out.println(stack.pop());  // 输出：3System.out.println(stack.peek()); // 输出：2System.out.println(stack.size()); // 输出：2System.out.println(stack.isEmpty()); // 输出：false}
}

上述示例展示了栈的基本操作，包括入栈、出栈、查看栈顶元素、获取栈的大小以及检查栈是否为空。

代码

public String simplifyPath(String path) {String[] split = path.split("/");Stack<String> stack = new Stack<>();Arrays.stream(split).forEach(s -> {if (s.equals("..")) {if (!stack.isEmpty()) {stack.pop();}} else if (!s.equals(".") && !s.equals("")) {stack.push(s);}});if (stack.size() > 0) {String lastElement = stack.lastElement();if (lastElement.equals("/")) {stack.remove(stack.size() - 1);}}StringBuilder sb = new StringBuilder();for (String s : stack) {sb.append("/").append(s);}return sb.toString().length() == 0 ? "/" : sb.toString();
}