本文主要是介绍[算法与数据结构] - No.8 图论(1)- 图的表示与遍历,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
在我们对图进行表示的时候,有两种邻接矩阵和邻接表两种表示:
1. 图的表示
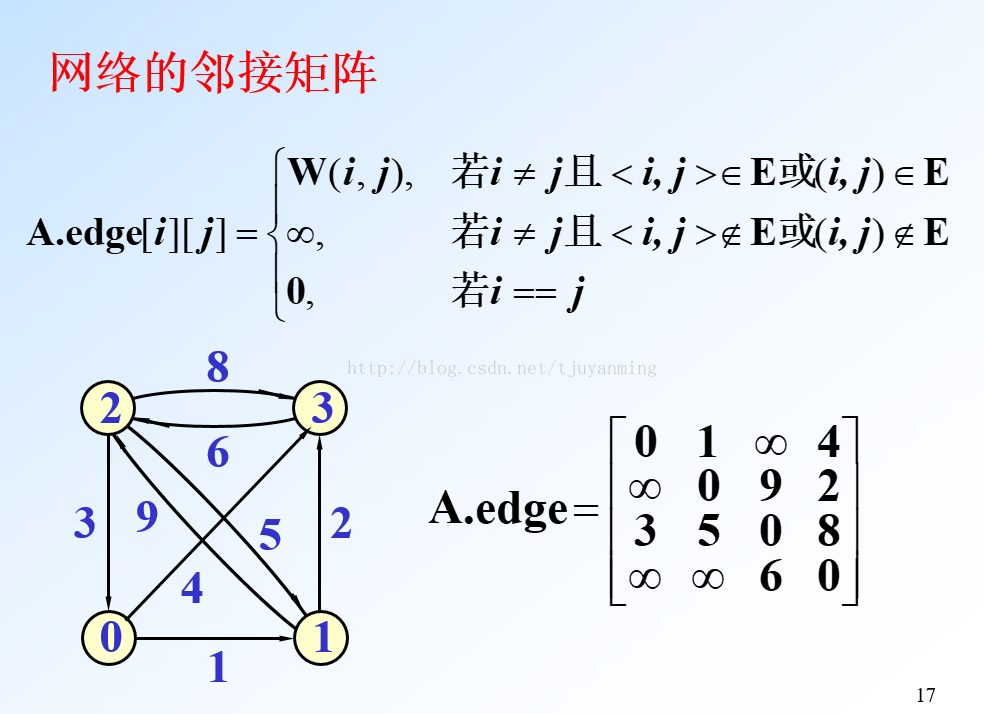
邻接矩阵:在一个矩阵matrix中,matrix[i][j]表示边<i,j>,在无权值的图中,其表示是i,j中是否有边;在有权值的图中,其表示i,j的权值
#include <iostream>using namespace std;int main()
{int matrix[100][100];int n,e;cout<<"请输入图的顶点数和边数(顶点从0开始):"<<endl;cin>>n>>e;for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i==j)matrix[i][j] = 0;elsematrix[i][j] = -1;}}for(int k=0;k<e;k++){int from,to;cout<<"请输入第"<<k<<"条边:"<<endl;cin>>from>>to;matrix[from][to] = 1;matrix[to][from] = 1;}for(int i=0;i<n;i++){for(int j=0;j<n;j++){cout<<matrix[i][j]<<" ";}cout<<endl;}}
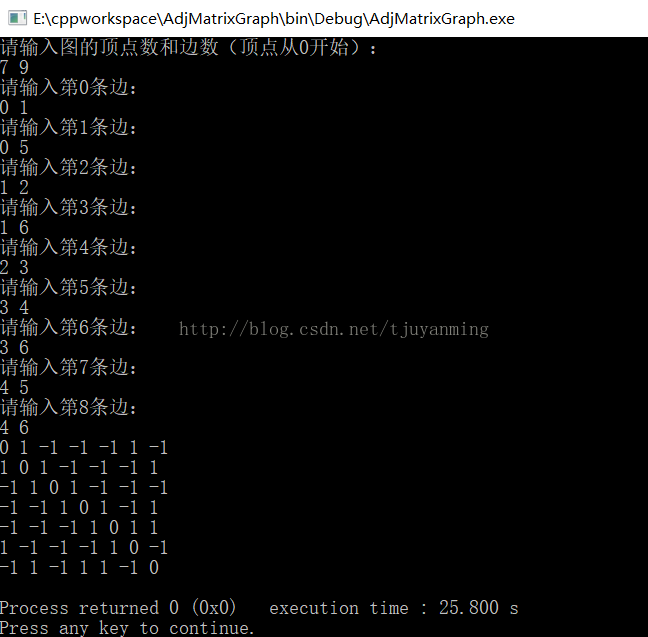
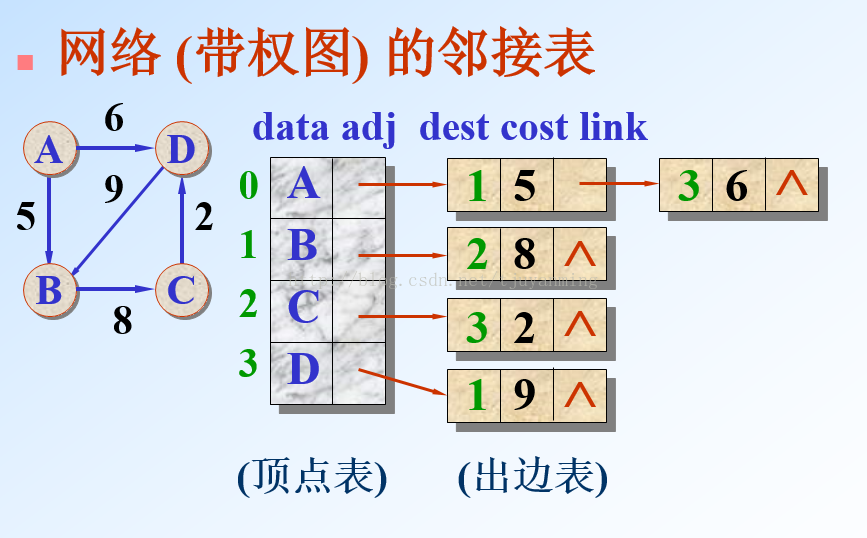
邻接表:
#include <iostream>
#include <stdio.h>
#include <stdlib.h>#define MaxVertexNum 50
using namespace std;typedef struct AdjNode{int vertex;struct AdjNode *nextNode;
}AdjNode,*PAdjNode;typedef struct Node{int vertex;PAdjNode firstNode;
}Node,*PNode;typedef struct Graph{int n;int e;PNode adjList;
}ALGraph,*PALGraph;
void createGraph(PALGraph G)
{int n,e;cout<<"请输入图的顶点数和边数(顶点从0开始):"<<endl;cin>>n>>e;G->n = n;G->e = e;for(int i=0;i<n;i++){G->adjList[i].vertex = i;G->adjList[i].firstNode = NULL;}for(int j=0;j<G->e;j++){cout<<"请输入第"<<j<<"条边:"<<endl;int startIndex,endIndex;cin>>startIndex>>endIndex;PAdjNode newNode = (PAdjNode)malloc(sizeof(AdjNode));newNode->vertex=endIndex;newNode->nextNode = G->adjList[startIndex].firstNode;G->adjList[startIndex].firstNode = newNode;}
}
int main()
{PALGraph G = (PALGraph)malloc(sizeof(ALGraph));G->adjList = (PNode)malloc(sizeof(Node)*1000);createGraph(G);for(int i=0;i<G->n;i++){int from = G->adjList[i].vertex;PAdjNode temp = G->adjList[i].firstNode;while(temp!=NULL){int to = temp->vertex;cout<<from<<"->"<<to<<endl;temp = temp->nextNode;}}
}
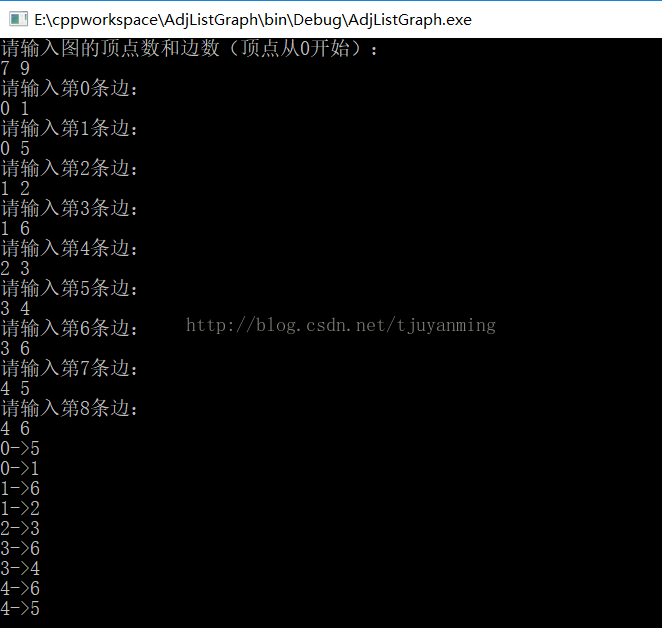
2. 图的遍历
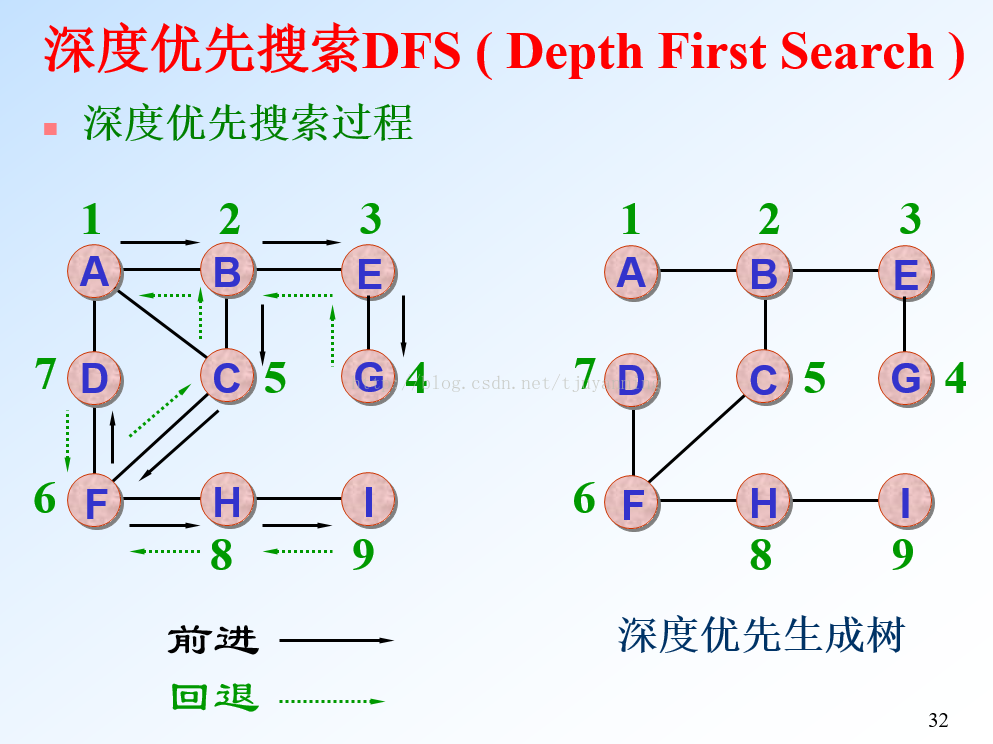
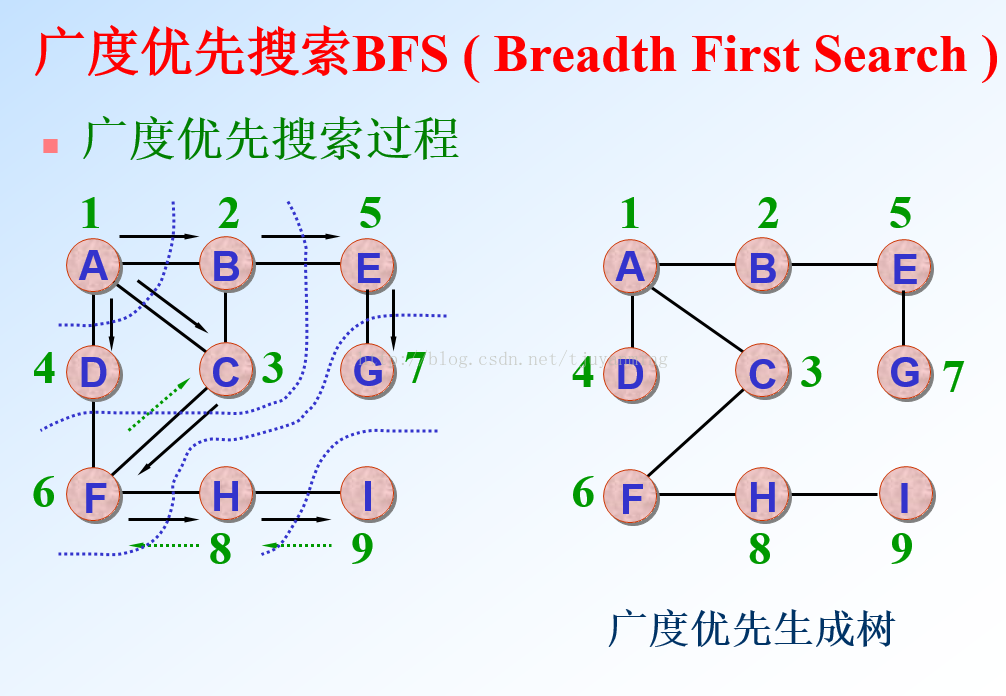
图的遍历分为深度优先和广度优先(我们以邻接矩阵为例)
算法实现(将上图的ABC...替换为0.1.2.3.....):
#include <iostream>using namespace std;
int n,e;
void DFS(int visited[],int m[][100],int i)
{if(visited[i]!=1){cout<<i<<" ";visited[i] = 1;for(int k = 0;k<n;k++){if(m[i][k]!=-1){DFS(visited,m,k);}}}
}
int main()
{int matrix[100][100];int visited[100] = {0};cout<<"请输入图的顶点数和边数(顶点从0开始):"<<endl;cin>>n>>e;for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i==j)matrix[i][j] = 0;elsematrix[i][j] = -1;}}for(int k=0;k<e;k++){int from,to;cout<<"请输入第"<<k<<"条边:"<<endl;cin>>from>>to;matrix[from][to] = 1;matrix[to][from] = 1;}/*for(int i=0;i<n;i++){for(int j=0;j<n;j++){cout<<matrix[i][j]<<" ";}cout<<endl;}*/DFS(visited,matrix,0);}
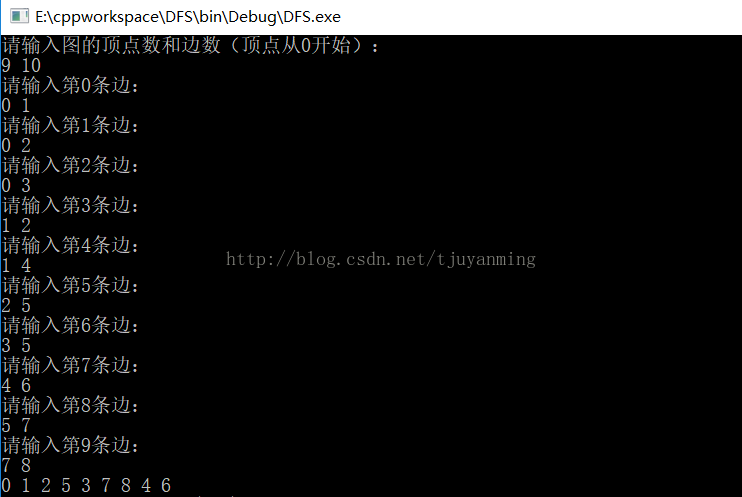
算法实现:
#include <iostream>
#include <queue>
using namespace std;
int n,e;
void BFS(int visited[],int m[][100],int i)
{queue<int>myqueue;while(!myqueue.empty()){myqueue.pop();}myqueue.push(i);while(!myqueue.empty()){int node = myqueue.front();myqueue.pop();if(visited[node]!=1){cout<<node<<" ";visited[node] = 1;}for(int k = 0; k<n; k++){if(m[node][k] == 1&&visited[k]!=1){myqueue.push(k);}}}}
int main()
{int matrix[100][100];int visited[100] = {0};cout<<"请输入图的顶点数和边数(顶点从0开始):"<<endl;cin>>n>>e;for(int i=0;i<n;i++){for(int j=0;j<n;j++){if(i==j)matrix[i][j] = 0;elsematrix[i][j] = -1;}}for(int k=0;k<e;k++){int from,to;cout<<"请输入第"<<k<<"条边:"<<endl;cin>>from>>to;matrix[from][to] = 1;matrix[to][from] = 1;}BFS(visited,matrix,0);}
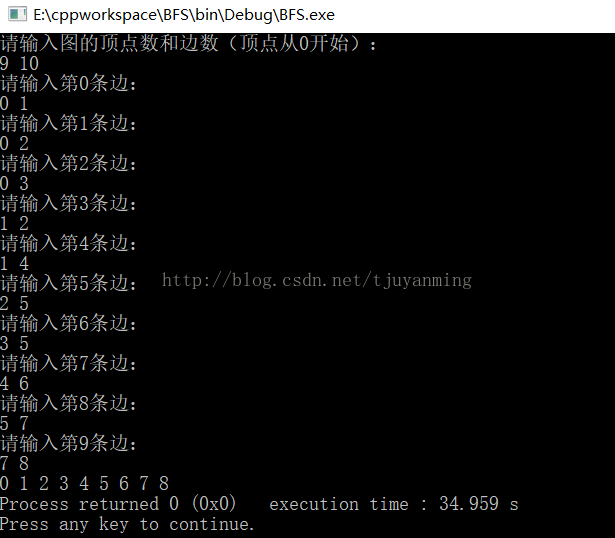
P.S. 文章不妥之处还望指正
这篇关于[算法与数据结构] - No.8 图论(1)- 图的表示与遍历的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!