龙书D3D11章节习题答案(第十章)

本文主要是介绍龙书D3D11章节习题答案(第十章)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

以下答案仅供参考，有错欢迎留言。

Chapter 10 : Stenciling

1. Prove that the general shadow matrix S reduced to Sdir if Lw = 0 and S reduces to Spoint for Lw = 1.

P.833~834的C.4.7 Ray/Plane Intersection给出了S的推导过程，Sdir和Spoint唯一的区别在于Sdir所用的L为(Lx,Ly,Lz,0), 而Spoint所用的L为(Lx,Ly,Lz,1)，为了在处理阴影时统一用一个Shadow Matrix计算，引入Lw来表示0和1，具体证明可用笔验算。

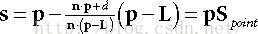
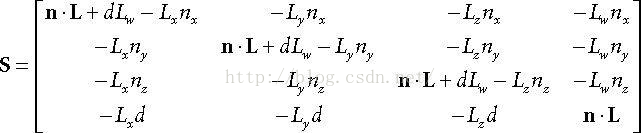
2. Prove that  by doing the matrix multiplication for each component, as was done in §10.5.1 for directional lights.

 // Lw=1

首先把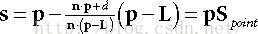变形为s = (-p*n·(p-L) + (n·p+d)*(p-L))/(-n·(p-L))

由S’ = [Px, Py, Pz, 1] * S，

Sw = -PxNx - PyNy - PzNz + n·L= -n·(p-L)， 

即上式的分母(在投影到齐次空间w=1上时会自动做除法，所以接下来只要证明[Px, Py, Pz, 1] * S计算得出的分子与公式变形得到的分子(-p*n·(p-L) + (n·p+d)*(p-L))是相同的即可)。

将分子(-p*n·(p-L) + (n·p+d)*(p-L))

化简：-p*n·p + p*n·L + n·p*p - n·p*L + d*p - d*L = p*n·L - L*n·p + d*p - d*L = p*(n·L+d) - L*(n·p+d)

由S’ = [Px, Py, Pz, 1] * S，

Si = Pi*(n·L + d) - Li*(PxNx+PyNy+PzNz+d) = Pi*(n·L + d) - Li*(n·p + d), 

即计算所得的Si与上述由分子得到的化简式相同，证毕。

这篇关于龙书D3D11章节习题答案(第十章)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---