LC 501.二叉搜索树中的众数

本文主要是介绍LC 501.二叉搜索树中的众数，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

501.二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有众数（即，出现频率最高的元素）。

如果树中有不止一个众数，可以按 任意顺序 返回。

假定 BST 满足如下定义：

结点左子树中所含节点的值 小于等于 当前节点的值
结点右子树中所含节点的值 大于等于 当前节点的值
左子树和右子树都是二叉搜索树

示例 1：

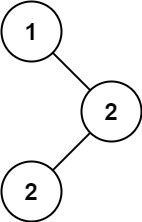
输入： root = [1,null,2,2]
输出：[2]

示例 2：

输入： root = [0]
输出：[0]

提示：

树中节点的数目在范围 $1, 10^4]$ 内
$-10^5 \leq Node.val \leq 10^5$

进阶： 你可以不使用额外的空间吗？（假设由递归产生的隐式调用栈的开销不被计算在内）

解法一(递归 + 中序遍历)

思路分析：

首先题目给出二叉搜索树的定义，因此可以使用中序遍历来遍历二叉树，从而得到一个有序的序列，然后根据该有序的序列寻找众数。
使用递归的方式来实现二叉搜索树的中序遍历
同时对于递归的返回值，为null，递归的参数则有二叉树的节点
对于递归的边界条件，若二叉树的节点为null，结束递归
对于递归的一般过程；则对该节点的值进行统计与判断
1. 首先需要一个全局变量val来记录上一个节点的值，初始为root.val，然后使用一个全局变量num来统计对应val值出现的次数，初始为0
2. 当遍历到某节点时，若该节点的值node.val == val，则++ num
3. 若该节点的值不等于val，则将已经统计记录的val和num进行判断，另一个全局变量maxNum用于记录出现某值的最大次数
  1. 若num > maxNum，则出现新的众数，重新记录保存val
  2. 若num == maxNum，则将该众数继续保存到已有的记录中
  3. 若num < maxNum，则无需操作
4. 当判断记录结束后，更新val和num

实现代码如下：

class Solution {int val;	// 用于记录中序遍历上一个节点的值int num;	// 用于记录值等于val的节点个数int maxNum;	// 用于记录num出现的最大值List<Integer> ans;	// 用于保存记录出现的众数public int[] findMode(TreeNode root) {val = root.val;	// 初始化为根节点ans = new LinkedList<>();doFindMode(root);updateAns();	// 再进行更新ans 防止漏掉序列最后连续的数值int[] arr = new int[ans.size()];for (int i = 0; i < ans.size(); ++ i) {arr[i] = ans.get(i);}return arr;}private void doFindMode(TreeNode node) {if (node == null)return ;doFindMode(node.left);		// 遍历左子树if (node.val == val) {++ num;} else {updateAns();	// 对列表进行更新val = node.val;num = 1;}doFindMode(node.right);		// 遍历右子树}private void updateAns() {if (num > maxNum) {ans.clear();	// 清除记录ans.add(val);	// 记录新的众数maxNum = num;	// 更新最大num} else if (num == maxNum) {ans.add(val);	// 增加新的众数}}
}