15.java openCV4.x 入门-Core之广义矩阵乘法运算

本文主要是介绍15.java openCV4.x 入门-Core之广义矩阵乘法运算，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

专栏简介
💒个人主页 📰专栏目录 点击上方查看更多内容	📖心灵鸡汤📖 我们唯一拥有的就是今天，唯一能把握的也是今天 建议把本文当作笔记来看，据说专栏目录里面有相应视频🤫	🧭文章导航🧭 ⬆️ 14.Core之图像融合 ⬇️ 16.Core之图像变换

  

一、广义矩阵乘法

   gemm其名称来源于 “General Matrix Multiply”，即广义矩阵乘法。此方法与matMul()方法有一样的作用，不过此方法支持第三个矩阵。

1. 字段

GEMM_1_T	这是矩阵乘法的一种变换方式，表示对第一个矩阵进行转置
GEMM_2_T	表示对第二个矩阵进行转置.
GEMM_3_T	表示对第三个矩阵进行转置.

2.方法介绍

gemm​(Mat src1, Mat src2, double alpha, Mat src3, double beta, Mat dst, int flags)
参数：
src1	第一个要进行乘法的输入矩阵，可以是实数类型（CV_32FC1，CV_64FC1）或复数类型（CV_32FC2，CV_64FC2）
src2	第二个与src1相同类型的要进行乘法的输入矩阵
alpha	矩阵乘积的缩放因子
src3	第三个可选的增量矩阵，添加到矩阵乘积中；它应该与src1和src2具有相同类型
beta	src3的权重
dst	输出矩阵；它具有适当的尺寸，并且与输入矩阵具有相同的类型.
flags	操作标志. GEMM_*。（支持组合 G1+G2）

   gemm(src1, src2, alpha, src3, beta, dst, GEMM_1_T + GEMM_3_T)

   对应的数学表达式为:$\text{dst}=\text{alpha}\cdot {\text{src1}}^T\cdot \text{src2}+\text{beta}\cdot {\text{src3}}^T$。
   其中${\text{src1}}^T和{\text{src3}}^T$分别表示$\text{src1}和\text{src3}$转置

3.算法说明

   算法涉及到实数矩阵和复数矩阵

1.算法规则

   1.结果矩阵的行数等于第一个矩阵的行数，列数等于第二个矩阵的列数。如果 (A) 是一个 $(m\times n)$ 的矩阵，(B) 是一个 $(n\times p)$ 的矩阵，则结果矩阵 © 是一个 $(m\times p)$ 的矩阵。
   2.结果矩阵中的每个元素 $(c_{ij})$ 是由第一个矩阵 (A) 的第$(i)$ 行与第二个矩阵 (B) 的第$(j)$ 列对应元素相乘后相加得到的。即：

   $[C_{ij}={\sum }_{k=1}^n{A}_{ik}\cdot B_{kj}]$

,其中 $(1\le i\le m)，(1\le j\le p)，(1\le k\le n)，i是行索引，j是列索引，k为1到n之间的值$
   3.矩阵乘法并不满足交换律，即A×B不一定等于B×A，除非矩阵A和B是方阵（即行数和列数相等）且是可交换的。

2.实数矩阵（单通道）

   1.计算 $(C_{ij})$ 的值，即将第一个矩阵 A的第 $i$ 行与第二个矩阵 B 的第 $j$ 列对应元素相乘后相加得到。
   2.将计算结果赋值给结果矩阵C的对应位置。

示例一：

        Mat A =  new Mat(2,3, CvType.CV_32FC1);A.put(0,0,1,2,3,4,5,6);Mat B = new Mat(3,2,CvType.CV_32FC1 );B.put(0,0,3,4,5,6,7,8);Mat C= new Mat();/Core.gemm(A,B,1,new Mat(),1,C);System.out.println("A.dump() = \n"  + A.dump());System.out.println("B.dump() = \n" + B.dump());System.out.println("C.dump() = \n" + C.dump());

结果：

A.dump() = 
[1, 2, 3;4, 5, 6]
B.dump() = 
[3, 4;5, 6;7, 8]
C.dump() = 
[34, 40;79, 94]

计算如下：

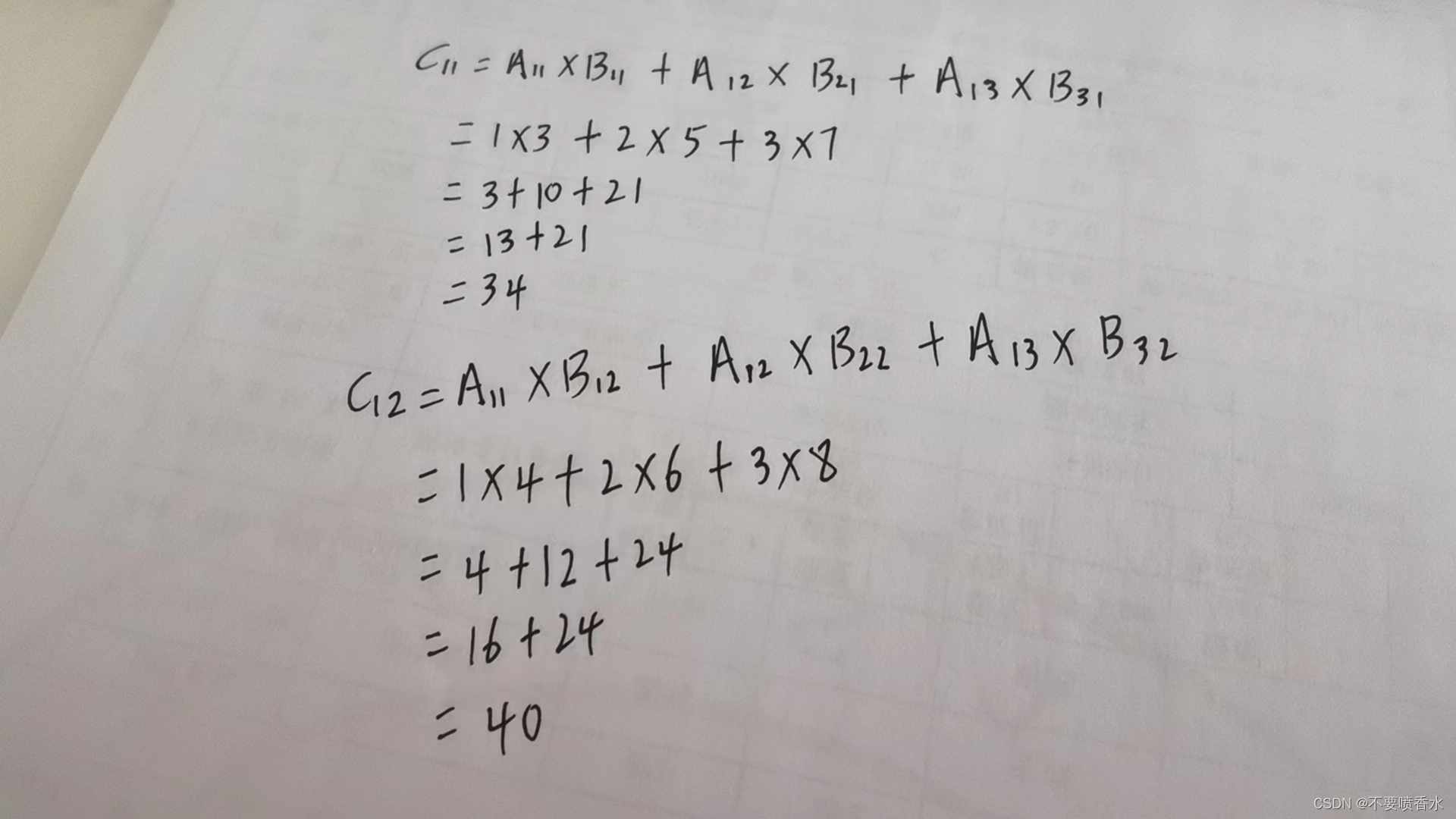
然后依次计算出位置的值即可。
示例二、

        Mat src1 =  new Mat(2,3, CvType.CV_32FC1);src1.put(0,0,1,2,3,4,5,6);Mat src2 = new Mat(3,2,CvType.CV_32FC1 );src2.put(0,0,3,4,5,6,7,8);Mat dst = new Mat();Mat src3 = new Mat(3,3,CvType.CV_32FC1);src3.put(0,0,1,2,3,4);Core.gemm(src1,src2,2,src3,1,dst,Core.GEMM_1_T+Core.GEMM_2_T);System.out.println("src1.dump() = \n"  + src1.dump());System.out.println("src2.dump() = \n" + src2.dump());System.out.println("dst.dump() = \n" + dst.dump());

请自行验证结果

3.复数矩阵（双通道）

   对于复数（双通道）数据，它的计算和计算实数矩阵相似，只需要按照复数的计算规则计算即可:
$(a+bi)\ast (c+di)=(ac-bd)+(ad+bc)i$，
其中，$a,b,c,d$ 都是实数，$i$ 是虚数单位。

        System.loadLibrary(Core.NATIVE_LIBRARY_NAME);Mat A =  new Mat(1,2, CvType.CV_32FC2);A.put(0,0,1,2,3,4 );Mat B = new Mat(2,1,CvType.CV_32FC2 );B.put(0,0,3,4,5,6);Mat C= new Mat();Core.gemm(A ,B,new Mat(),1,C);System.out.println("A.dump() = \n"  +  A.dump());System.out.println("B.dump() = \n" + B.dump());System.out.println("C.dump() = \n" + C.dump());

结果

A.dump() = 
[1, 2, 3, 4]
B.dump() = 
[3, 4;5, 6]
C.dump() = 
[-14, 48]

   计算方式如下,

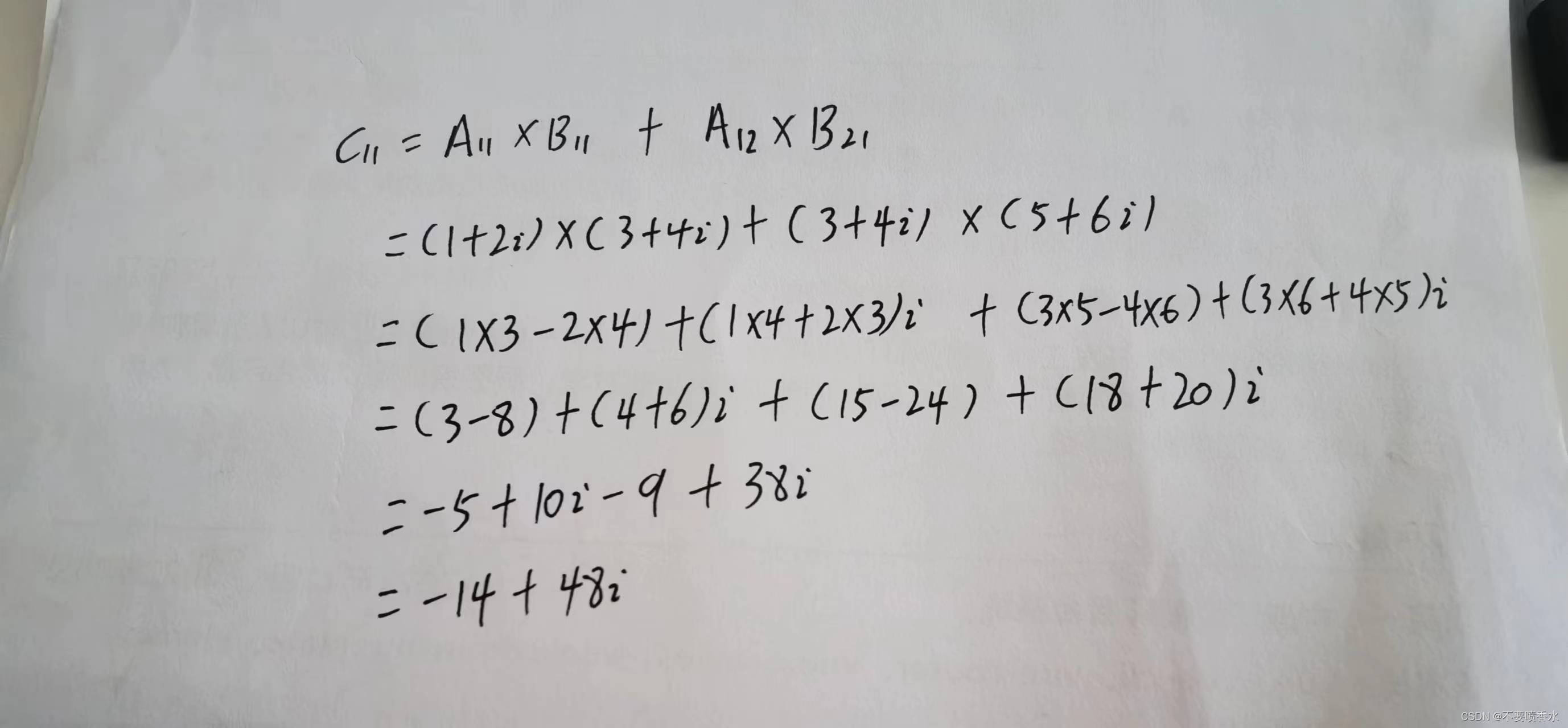
   按照这个方式计算其它位置的值即可。

这篇关于15.java openCV4.x 入门-Core之广义矩阵乘法运算的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---