K近邻法（KNN）学习笔记(used by python matlab)

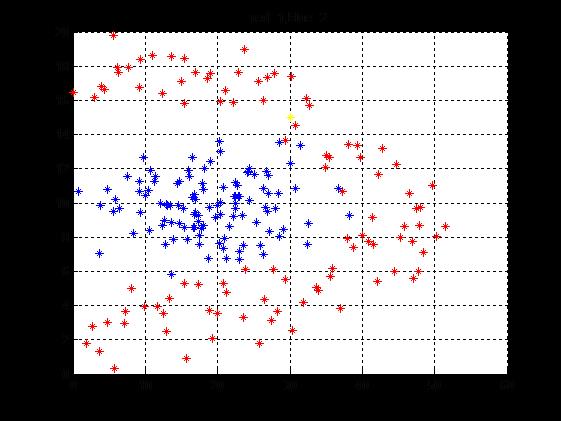
本文主要是介绍K近邻法（KNN）学习笔记(used by python matlab)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. K 近邻法，简单的说，就是给定一个训练数据集，对新的输入实例，在训练数据集中找到与该实例最邻近的k个实例，这k个实例的多数属于某个类，就把该输入实例分为这个类。
图示说明
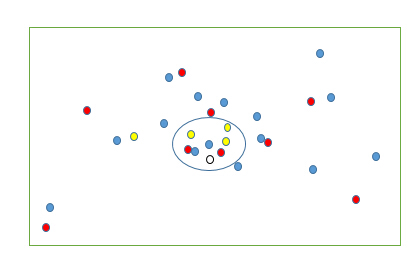
2. 模型：
三要素：距离度量、k值的选择和分类判决规则
2.1 距离度量
定义 $x_i$ 和 $x_j$ 之间的距离为：

L p (x i, x j) = (\sum l | x l i - x l j | p) 1 / p

$L_p(x_i,x_j)=(\sum_l|x_i^l-x_j^l|^p)^{1/p}$
当P=2时，为欧氏距离；当P=1时，为曼哈顿距离；当P=∞时，为各个坐标距离的最大值。
2.2 k值的选择

选择	优点	缺点
较小K值	减小近似误差	模型变得复杂可能发生过拟合
较大K值	减小估计误差，模型简单	近似误差增大

解决方式：交叉验证法
2.3 分类决策规则
多数表决规则，等价于，经验风险最小化。
2.4 代码演示（matlab实现）
matalab代码演示

%knearestneighbor 
%data=[1,1,1;1,1.1,1;0,0,2;0,1,2];
%testport=[0,0.1];
clear all;
testport=[30,15];
data = importdata('data.txt');
k=7;
[numbers,demins]=size(data);
record(:,1:demins-1)=data(:,1:demins-1);
label=data(:,demins);
dis=zeros(1,numbers);
for i=1:numbers
dis(i)=distancecount(testport,record(i,:),2);
end
Ddis=sort(dis);
array=find(dis<=Ddis(k));
[n1,n2]=size(array);
for i=1:n2types(i)=label(array(i));
end
if length(find(label==1))>length(find(label==2))ans =1
elseans =2
end
%distance calculate
function distances=distancecount(xi,xj,p)
distances=power(sum(power(abs(xi-xj),p)),1/p);

2.5 KNN UESD BY PYTHON
酒定价问题
已知：一组酒的年龄和等级以及对应的价格，如何求一瓶已知年龄等级的酒的价格？
求解：在数据中找出与这瓶酒相近规格的酒，对这些酒的价格取平均。
分析：
（1）找多少瓶酒？（K值选择）
（2）如何量化相近规格？（距离度量）
（3）价格如何平均？（直接平均Or加权平均）
提升篇：
（1）如果变量不止年龄和等级，还包括出厂通道，尺寸等等？结果又会如何？（模型对不同类型的变量的适用问题）
（2）如果数据来源不是同一处，如折扣店购买等等，那么平均价格的意义有所削减，那么结果如何修改？（概率分布问题）

（1）K值选择
如前文所说，k 值选择影响到结果的准确性，k选太小则对噪声敏感，k选太大会使得结果过于平滑。
衡量K值的选择方法是：交叉验证 cross-validate
数据集=训练集+测试集

直接交叉验证
以一定概率随机选择若干条数据作为测试集，由训练集得到的模型用测试集验证。Python代码如下：

def dividedata(data,test=0.05):trainset=[]testset=[]for row in data:if random()<test:testset.append(row)else:trainset.append(row)return trainset,testsetdef testalgorithm(algf,trainset,testset):error=0.0for row in testset:ans=algf(trainset,row['input'])error+=(row['result']-ans)**2return error/len(testset)def crossvalidate(algf,data,trials=100,test=0.05):error=0.0for i in range(trials):trainset,testset=dividedata(data,test)error+=testalgorithm(algf,trainset,testset)return error/trials

留一式交叉验证
将数据集的每一行单独看做一个测试集，并将数据集的剩余部分都看做训练集。python代码如下：

#leave-one-out
def divideone(data,row1):trainset=[]testset=[]for row in data:if row==row1:testset.append(row)else:trainset.append(row)return trainset,testsetdef crossvalidate1(algf,data):error=0.0for row in data:trainset,testset=divideone(data,row)error+=testalgorithm(algf,trainset,testset)return error/len(data)

测试结果：

value	direct	leave-one-out
k=1	638.15	633.45
k=3	458.99	478.23
k=5	472.71	450.13

（2）距离度量
前文已经提到，不再赘述。给出欧式距离的python代码：

def euclidean(v1,v2):d=0.0for i in range(len(v1)):d+=(v1[i]-v2[i])**2return math.sqrt(d)

（3）价格平均问题
i 直接平均

def knnestimate(data,vec1,k=5):dlist=getdistances(data,vec1)avg=0.0for i in range(k):idx=dlist[i][1]avg+=data[idx]['result']avg=avg/kreturn avg

ii. 加权平均
由于算法可能会选择距离太远的近邻，补偿的办法就是根据距离的远近赋予相应的权重。
有三种方法：

Inverse Function
$w=1/(distance+const)$
Subtraction Function
$w=const-distance,distance<const$
$w=0,distance>const$
Gaussian Function
$w=e^{-distance^2/(2\sigma^2)}$

加权方式：
$ans=\sum{w_id_i}/\sum{w_i}$
（4）不同变量的问题
i. 按比例缩放

def rescale(data,scale):scaleddata=[]for row in data:scaled=[scale[i]*row['input'][i] for i in range(len(scale))]scaleddata.append({'input':scaled,'result':row['result']})return scaleddata

ii. 优化缩放比例（等研究完优化问题再来补充）
（5）概率分布问题

def probguess(data,vec1,low,high,k=5,weightf=gaussian):dlist=getdistances(data,vec1)
#print dlistnweight=0.0tweight=0.0for i in range(k):dist=dlist[i][0]idx=dlist[i][1]weight=weightf(dist)v=data[idx]['result']if v>=low and v<=high:nweight+=weighttweight+=weightif tweight==0:return 0return nweight/tweightdef cumulativegraph(data,vec1,high,k=5,weightf=gaussian):t1=arange(0.0,high,0.1)cprob=array([probguess(data,vec1,0,v,k,weightf) for v in t1])plot(t1,cprob)
#show()def prograph(data,vec1,high,k=5,ss=5.0,weightf=gaussian):t1=arange(0.0,high,0.1)probs=[probguess(data,vec1,v,v+0.1,k,weightf) for v in t1]smooted=[]for i in range(len(probs)):sv=0.0for j in range(0,len(probs)):dist=abs(i-j)*0.1weight=gaussian(dist,sigma=ss)sv+=weight*probs[j]smooted.append(sv)smooted=array(smooted)plot(t1,smooted)
#show()

累积概率图

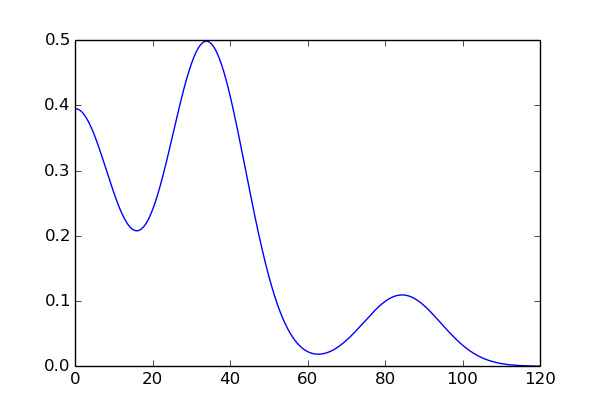
ss=5的概率密度图

ss=1的概率密度图

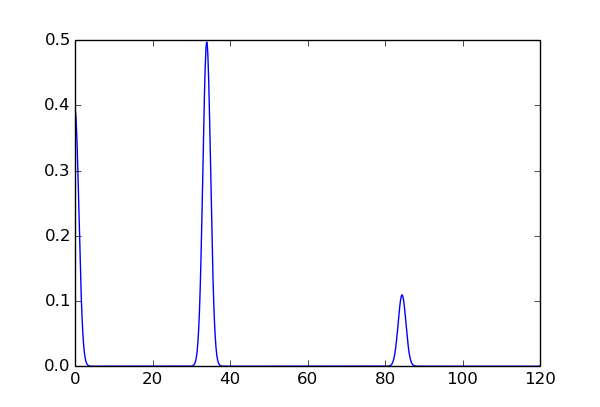
ss=10的概率密度图

链接：
K近邻分类算法实现 in Python
用Python开始机器学习（4：KNN分类算法）
参考书目：
李航《统计学习方法》
附录：
data.txt数据
（数据来源：http://blog.sina.com.cn/s/blog_8bdd25f80101d93o.html）
1.8796 1.8041 1.0000
2.6801 2.7526 1.0000
3.6284 1.3313 1.0000
4.7302 3.0267 1.0000
5.7865 0.3089 1.0000
7.1831 2.9453 1.0000
7.2395 3.6268 1.0000
8.0763 4.9714 1.0000
9.9172 3.9551 1.0000
11.7397 3.9500 1.0000
12.8685 2.4619 1.0000
12.5289 3.5313 1.0000
13.3206 4.4376 1.0000
15.7457 0.9094 1.0000
15.4758 5.2898 1.0000
17.2917 5.2197 1.0000
18.9338 3.7324 1.0000
19.3299 2.0778 1.0000
20.7408 5.2698 1.0000
20.0199 3.5670 1.0000
21.2740 4.7658 1.0000
23.6375 3.3211 1.0000
23.8603 6.1293 1.0000
25.7806 1.8003 1.0000
26.4698 4.3295 1.0000
27.3746 3.1499 1.0000
27.6922 6.1123 1.0000
28.3321 3.6388 1.0000
29.3112 5.5035 1.0000
30.3822 2.5172 1.0000
31.8449 4.1858 1.0000
33.7120 5.0515 1.0000
33.9805 4.8947 1.0000
35.6319 5.7023 1.0000
35.9215 6.1456 1.0000
36.9147 3.8067 1.0000
37.9014 7.9138 1.0000
38.8244 7.3828 1.0000
40.8032 7.7581 1.0000
40.0112 8.0748 1.0000
41.5948 7.5525 1.0000
42.0983 5.4144 1.0000
44.3864 5.9879 1.0000
45.3002 7.9712 1.0000
46.9660 7.7468 1.0000
47.1053 5.5875 1.0000
47.8001 5.9673 1.0000
48.3976 7.1165 1.0000
50.2504 8.0479 1.0000
51.4667 8.6202 1.0000
49.7518 11.0474 1.0000
48.0198 9.7412 1.0000
47.8397 8.6673 1.0000
47.5073 9.6810 1.0000
46.5877 10.5484 1.0000
45.8399 8.6472 1.0000
44.6894 12.2699 1.0000
42.7355 13.1906 1.0000
42.2416 11.6802 1.0000
41.4626 9.1437 1.0000
39.3878 13.3631 1.0000
39.8096 12.6606 1.0000
38.1384 13.4300 1.0000
37.2636 10.7010 1.0000
35.4688 12.6869 1.0000
35.0976 12.7679 1.0000
34.8632 12.0533 1.0000
32.6704 15.7258 1.0000
32.3111 16.0957 1.0000
30.7838 14.5081 1.0000
30.2546 17.3737 1.0000
29.3982 13.6487 1.0000
27.7944 17.5663 1.0000
26.8273 17.3489 1.0000
26.3104 15.9892 1.0000
25.6752 17.1196 1.0000
23.7432 19.0045 1.0000
22.8505 17.6571 1.0000
22.1893 15.8862 1.0000
21.1315 16.5870 1.0000
20.4331 15.9183 1.0000
19.0226 17.5691 1.0000
18.5528 17.2806 1.0000
16.9787 17.6517 1.0000
15.3718 18.4702 1.0000
15.4013 15.8341 1.0000
14.9654 17.0939 1.0000
13.6133 18.5902 1.0000
12.4071 16.4305 1.0000
10.9699 18.6493 1.0000
9.2292 16.7441 1.0000
9.3297 18.4027 1.0000
7.7307 17.9292 1.0000
6.2801 17.6374 1.0000
6.1335 17.9167 1.0000
5.6460 19.7987 1.0000
4.3479 16.6548 1.0000
3.9989 16.7955 1.0000
2.9233 16.1468 1.0000
0.1177 16.4696 1.0000
18.0917 10.7906 2.0000
20.8946 7.9302 2.0000
27.0622 11.5962 2.0000
5.5730 9.4899 2.0000
26.7574 11.8636 2.0000
16.7292 9.3432 2.0000
19.0151 12.4156 2.0000
24.3078 11.8160 2.0000
22.4947 10.3850 2.0000
9.3145 9.4613 2.0000
9.9780 10.4605 2.0000
22.4415 9.6565 2.0000
13.5368 9.8577 2.0000
9.2123 11.2597 2.0000
16.8452 8.5662 2.0000
16.6143 8.5577 2.0000
12.0322 9.9863 2.0000
12.3410 8.6917 2.0000
20.7440 7.3164 2.0000
7.5386 11.5666 2.0000
26.8886 9.5218 2.0000
22.9919 7.1799 2.0000
17.3493 9.2897 2.0000
18.8619 9.7411 2.0000
13.5521 5.7984 2.0000
12.7381 7.5564 2.0000
21.2411 6.7318 2.0000
24.4092 11.9952 2.0000
26.6712 9.7442 2.0000
18.2293 12.0030 2.0000
22.6769 11.0067 2.0000
30.7391 10.8611 2.0000
32.5980 8.7771 2.0000
16.7562 10.5129 2.0000
32.4282 7.6007 2.0000
18.0425 8.6968 2.0000
14.7803 8.8055 2.0000
22.3809 10.3572 2.0000
18.6982 6.7692 2.0000
25.9816 7.5022 2.0000
22.9529 10.3560 2.0000
9.6995 12.6448 2.0000
0.8253 10.6597 2.0000
22.2435 9.2030 2.0000
12.9460 9.9126 2.0000
24.4483 10.1399 2.0000
28.4938 13.5242 2.0000
13.1255 9.8689 2.0000
25.0474 11.6899 2.0000
19.9509 9.8567 2.0000
15.4784 8.5583 2.0000
28.4445 10.5570 2.0000
15.9001 11.8933 2.0000
26.3668 7.0044 2.0000
28.5033 8.0366 2.0000
6.4663 9.6549 2.0000
36.6973 10.8341 2.0000
27.1367 8.3365 2.0000
25.3004 8.8306 2.0000
14.3970 11.1212 2.0000
17.4541 7.5968 2.0000
10.7689 11.8858 2.0000
11.3941 11.5540 2.0000
13.6303 8.8437 2.0000
22.5345 11.1880 2.0000
30.0558 12.3294 2.0000
27.0878 10.5662 2.0000
16.0525 11.5472 2.0000
5.9346 10.2316 2.0000
20.4220 10.0298 2.0000
14.5875 9.8690 2.0000
8.3235 8.2102 2.0000
21.6882 8.6548 2.0000
22.4873 9.9445 2.0000
24.1396 11.7790 2.0000
17.4024 8.9218 2.0000
16.4952 12.6580 2.0000
17.7652 8.5352 2.0000
17.9541 11.1611 2.0000
20.3055 7.6421 2.0000
29.1058 8.4386 2.0000
19.7172 9.1464 2.0000
22.9040 10.4004 2.0000
31.4804 13.3684 2.0000
16.9647 10.1980 2.0000
23.3807 9.2596 2.0000
20.7638 10.9202 2.0000
13.9053 7.8416 2.0000
3.7968 9.8266 2.0000
4.7264 10.8025 2.0000
16.9223 9.4675 2.0000
15.3344 9.6976 2.0000
16.5509 10.3232 2.0000
10.5063 10.7580 2.0000
20.3627 13.0198 2.0000
20.2478 13.5945 2.0000
14.6817 11.2545 2.0000
23.5466 7.5405 2.0000
9.1412 10.6535 2.0000
12.6591 8.9793 2.0000
17.4900 8.1205 2.0000
11.2094 11.2549 2.0000
26.3995 10.8712 2.0000
27.9677 9.6512 2.0000
20.4156 9.3194 2.0000
10.5738 8.4045 2.0000
22.9527 6.6876 2.0000
3.6603 7.0692 2.0000
15.7903 7.8872 2.0000
38.2151 9.2523 2.0000