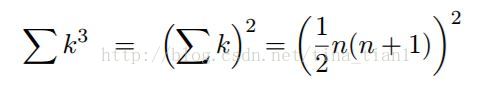本文主要是介绍1的平方加到n的平方公式, 1的立方加到n的立方公式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
证明:
利用公式 (n-1)3 = n3 -3n2 +3n-1
S3 = 13 +23 +33 +43 +...+n3
S2 = 12 +22 +32 +42 +...+n2
S1 = 1 +2 +3 +4+...+n
=>
S3-3S2+3S1-n = (1-1)3 + (2-1)3+ (3-1)3 + (4-1)3 + ... + (n-1)3 = S3 -n3
=>
3S2 = 3S1+n3 -n
而 S1= n(n+1)/2,
=>
S2 = n(n+1)(2n+1)/6
即: 12 +22 +32 +42 +...+n2 = n(n+1)(2n+1)/6
同理可推
相关:
(a+b)^n
=a^n+C(n,1)a^(n-1)b+C(n,2)a^(n-2)b^2+C(n,3)a^(n-3)b^3+……+C(n,n-2)a^2b^(n-2)+C(n,n-1)ab^(n-1)+b^n
杨辉三角
(a+b)0次方的系数 1
(a+b)1次方的系数 1 1
(a+b)2次方的系数 1 2 1
(a+b)3次方的系数 1 3 3 1
(a+b)4次方的系数 1 4 6 4 1
。。。
这篇关于1的平方加到n的平方公式, 1的立方加到n的立方公式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!