[paper note]LoRA+: 原理分析

本文主要是介绍[paper note]LoRA+: 原理分析，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

论文信息

论文标题：LoRA+: Efficient Low Rank Adaptation of Large Models

发表时间：2024年2月

论文内容

摘要

在本文中，我们表明，最初在论文《LoRA: Low-Rank Adaptation of Large Language Models》中引入的低秩适应（LoRA）会导致大宽度（嵌入维度）模型的次优微调。这是因为 LoRA 中的适配器矩阵 A 和 B 以相同的学习率更新。使用大宽度网络的缩放参数，我们证明对 A 和 B 使用相同的学习率并不能实现有效的特征学习。然后我们证明，只需通过精心选择的固定比率为 LoRA 适配器矩阵 A 和 B 设置不同的学习率，即可纠正 LoRA 的这种次优性。我们将此算法称为 LoRA+。在我们广泛的实验中，LoRA+ 提高了性能（1% ‑ 2% 的改进）和微调速度（高达 ~ 2 倍加速），而计算成本与 LoRA 相同。

主要结论

定理 1： （高效 LoRA（非正式））。假设权重矩阵 A 和 B 使用 Adam 进行训练，学习率分别为${\eta }_A$和${\eta }_B$。那么，不可能达到 ${\eta }_A={\eta }_B$ 的效率。然而，LoRA 微调在$η_A = θ(n^{-1} ) $ 和${\eta }_B=\theta (1)$时非常有效。

定理1的结果表明，只有一对满足$\frac{{\eta }_B}{{\eta }_A}=\theta (n)$的学习率才能实现效率。在实践中，这转化为设置${\eta }_B\gg {\eta }_A$，但在调整学习率时并不能提供固定的精确比率$\frac{{\eta }_B}{{\eta }_A}$ （“θ”中的常数通常很难处理），除非我们同时调整${\eta }_B$和${\eta }_A$ ，即从计算角度来看效率不高，因为它变成了 2D 调整问题。因此，很自然地设置一个固定的比率$\frac{{\eta }_B}{{\eta }_A}$并仅调整${\eta }_A$ （或${\eta }_B$），这将有效地将调整过程减少为一维网格搜索，实现与A、B学习率相同的标准 LoRA 的计算成本相当。我们将这种方法称为 LoRA+。

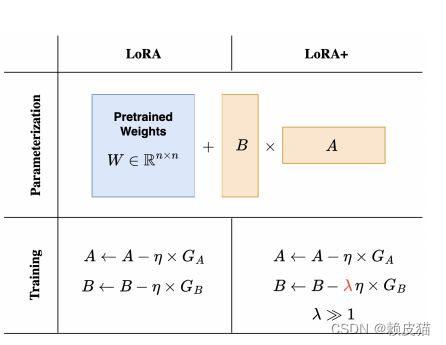
LoRA+ ：设置 LoRA 模块 A、B 的学习率，使得${\eta }_B=\lambda {\eta }_A$，其中 λ > 1 固定并调整${\eta }_A$。

在 LoRA+ 中，比率 λ 的选择至关重要。接近 1 的比率将类似标准 LoRA，而当 $n ≫ r $ 时，选择 $\lambda \gg 1$ 会改善结果。通过广泛的实证评估，我们首先验证我们的理论结果，并表明最优对$({\eta }_A,{\eta }_B)$ （就测试精度而言）通常满足${\eta }_B\gg {\eta }_A$。然后，我们研究了 LoRA+ 的最佳比率 λ，并提出了一个默认比率，根据经验发现，与标准 LoRA 相比，该比率通常可以提高性能。

LoRA+中如何设置比率 $\lambda =\frac{{\eta }_B}{{\eta }_A}$ ？

最佳比率 λ 取决于架构和通过“θ”中的常数进行的微调任务（定理1）。这是这些渐近结果的局限性，因为它们没有提供有关任务和神经架构如何影响常数的任何见解。为了克服这一限制，我们采用经验方法来估计 λ 的合理值。

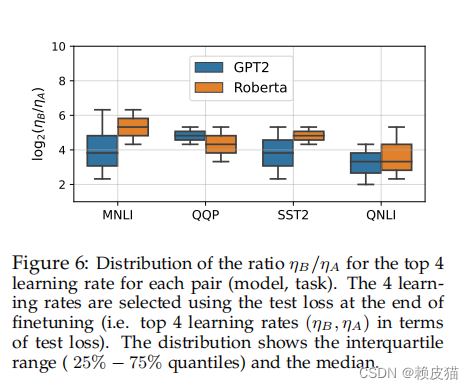
在上图中，显示了不同对（模型、任务）的测试精度方面前 4 次运行的$\frac{{\eta }_B}{{\eta }_A}$比率的分布。最佳比率对模型和任务敏感，但中位数对数比率徘徊在 4 左右。我们估计，通常设置一个比率$\lambda =\frac{{\eta }_B}{{\eta }_A}\approx 2$ 可以提高性能。这可以通过设置${\eta }_A=\eta$、 ${\eta }_B=2^4\eta$ 并调整超参数 η 来实现。

为了检查该方法的有效性，我们在 MNLI 任务上对 Roberta‑base 进行了 3 个时期的微调，使用两种不同的设置：

（LoRA+）${\eta }_B=2^4{\eta }_A$和（标准）${\eta }_B={\eta }_A$。在这两种设置中，我们通过网格搜索调整${\eta }_A$ 。

结果如下图所示

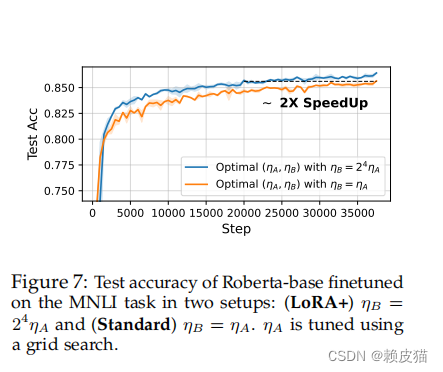
LoRA+（$\lambda =2^4$）显示出最终测试精度和训练速度的显着提高。使用 LoRA+，仅用 1.6 个 epoch，就达到了标准设置3个 epoch 后获得的最终精度。

从业者指南：使用LoRA+进行微调

将 LoRA+ 集成到任何微调代码中都很简单，只需从lora plus中提供的代码导入自定义训练器 LoraPlusTrainer，即可使用单行代码来实现。在Trainer中，λ 的值默认设置为 $ 2^{ 4}$ ，与 LoRA 相比，它可以显著提高性能。然而，请注意，λ 的最佳值取决于任务和模型：如果预训练模型的任务相对困难，则 λ 的选择将至关重要，因为需要有效的训练来使模型与微调任务保持一致。相反，当预训练模型的微调任务相对容易时，λ 的影响不太明显。根据经验，设置 $\lambda =2^4$是一个很好的起点。

结论和局限性

采用缩放参数，我们表明目前在实践中使用的 LoRA 微调效率不高。我们提出了一种方法 LoRA+，通过为 LoRA 适配器矩阵设置不同的学习率来解决这个问题。我们的分析得到了广泛的实证结果的支持，证实了 LoRA+ 在训练速度和性能方面的优势。这些好处对于“硬”任务更为显着，例如 Roberta/GPT2 的 MNLI（例如与 SST2 相比）和 LLama‑7b 的 MMLU（例如与 MNLI 相比）。然而，如图 7 （Figure 7） 所示，对最佳比率ηB/ηA的更精细估计应考虑任务和模型相关性，而我们在本文中的分析缺乏此维度。

这篇关于[paper note]LoRA+: 原理分析的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---