本文主要是介绍P4117 [Ynoi2018] 五彩斑斓的世界,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
分析第一个操作
朴素的做法,遍历一遍大于x就-=x,极限复杂度O(mn)
分块做法
整块:我们维护一个最大值,从mx到x遍历一遍(减去x)用并查集操作merge(i,i-x),考虑mx=100001,x=1,极限复杂度O(mV)
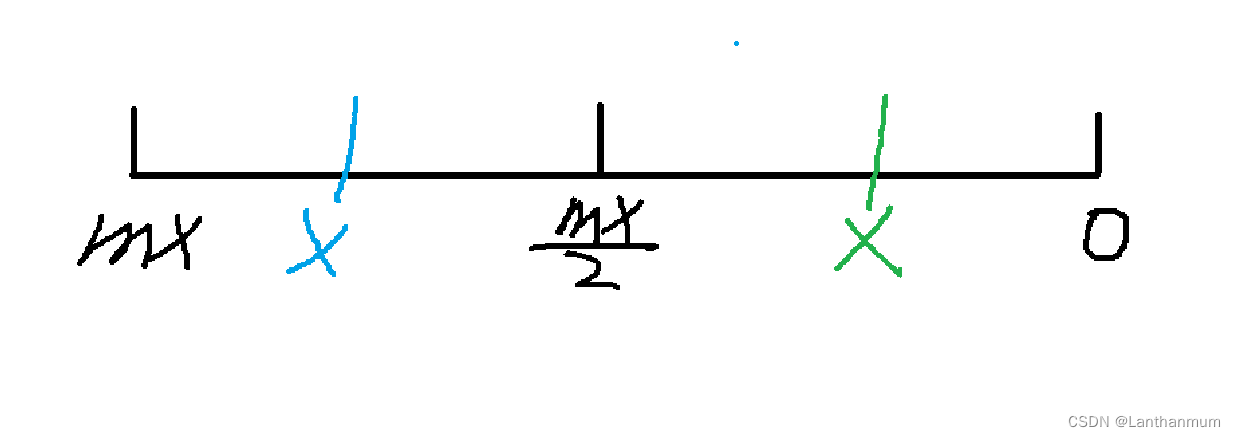
我们可以分析
1.x>(mx/2),从mx到x遍历一遍,应该是最优的复杂度O(mx-x)
2.x<(mx/2),最优的复杂度应该是O(x),因此思考在这种情况下如何操作使得复杂度为O(x),从x到0遍历一遍呗,我们可以遍历一遍x到0,merge(i,i+x),打上区间减法标记
3.x==(mx/2)都行
通过势能分析法总复杂度应该是O(sqrt(n)V) (我母鸡)(操作让区间最大值和区间最小值的差值变小,,值域缩小)
考虑每次都是x==(mx/2),且mx==V,O(V/2*sqrt(m))?
散块:暴力操作,再重构,无脑真不错,每次最多重构O(2*sqrt(n)),总共O(m*sqrt(n))
分析第二个操作
整块:直接得到并查集的大小
散块:遍历l到r,查询并查集==x,res++;
分析总时间复杂度O(Vsqrt(n)+msqrt(n)),快O(1e9),卡卡常啦
如果这样操作我们应该需要一个O(V*sqrt(n))数组,开不下这么大的数组;
lxl这个trick很妙啊
因为我们块与块之间没有关系,且时间挺多,可以离线下来,答案还有可加性,所以我们可以计算每个块的贡献这样只要开O(V)的数组即可
因此空间复杂度是O(V),1e6随便开
接下来,我们用代码实现一下。。。
先分析一下我们定义哪些数据
fa[N]并查集,index[V](存储该值的位置),val[N](存储该位置的值),num[V](存储该值的数量),lazy(减法懒标记),mx(最大值),ans[M](询问的答案)
int a[N];
int fa[N],index[V],num[V],val[N];//fa,该值的位置,大小,该位置的值
int L[B],R[B];//记录每个块的范围[l,r]
int ans[M];
int mx=-INF;
int lazy;//减法懒标记L,R(设为全局变量也行)
并查集2个操作
1.find
inline int find(int x){if(fa[x]==x){return x;}return fa[x]=find(fa[x]);
}2.merge
合并2个值的位置,2个值的数量,以及合并后要对原数组清空
inline void merge(int x,int y){if(index[y]){//值存在fa[index[x]]=index[y];//合并}else{//不存在index[y]=index[x];val[index[x]]=y;//赋值为y}num[y]+=num[x];//合并index[x]=0;//清空num[x]=0;//清空
}重构
重新维护一遍之前的量
inline void rebuild(int pos){//记录最大值,合并值,处理值的数量 mx=-INF;lazy=0;for(int i=L[pos];i<=R[pos];i++){mx=max(mx,a[i]);if(!index[a[i]]){index[a[i]]=i;fa[i]=i;val[i]=a[i];}else{fa[i]=index[a[i]];}num[a[i]]++;}
}操作一
1.整块
inline void modify(int x){//区间 O(V)if((x<<1)<=(mx-lazy)){//x*2<=mx,for(int i=lazy;i<=x+lazy;i++){//a[i]<=x 都加x,lazy+x;O(x);if(index[i]){merge(i,i+x);}}lazy+=x;}else{//2*x>mxfor(int i=mx;i>x+lazy;i--){//a[i]>x 减去x,O(mx-x);if(index[i]){merge(i,i-x);}}//最大的值可能有x,与原本的mx取小mx=min(mx,x+lazy);}
}min解释一下(我一开始不会),现在的情况是2*x>mx,可以转化成x>mx-x
分析2种情况
1.mx>x && x(数组中存在x),x
2.mx<x,mx
因此要取min
2.散块
我们要只需要下传懒标记,操作完重构一下即可
inline void update(int l,int r,int x,int pos){//下传lazyfor(int i=L[pos];i<=R[pos];i++){int temp=val[find(i)];a[i]=temp-lazy;index[temp]=0;num[temp]=0;}for(int i=L[pos];i<=R[pos];i++){val[i]=0;}l=max(l,L[pos]);r=min(r,R[pos]);//暴力操作for(int i=l;i<=r;i++){if(a[i]>x){ a[i]-=x;}}rebuild(pos);
}操作二
1.整块
直接加num[]
ans[j]+=num[que[j].x+lazy];2.遍历一遍
inline int query(int l,int r,int x,int pos){int res=0;l=max(l,L[pos]);r=min(r,R[pos]);for(int i=l;i<=r;i++){if(val[find(i)]-lazy==x){res++;}}return res;
}感觉询问比较轻松,主要是操作维护这块是难点
完整代码
#include<iostream>
#include<cmath>
#include<algorithm>
#include<cstring>
#include<vector>
#define INF 2147483647
using namespace std;
typedef long long ll;
const int N=1e6+9;
const int B=1e4+9;
const int V=1e5+9;
const int M=5e5+9;
namespace Lan {inline string sread() {string s=" ";char e=getchar();while(e==' '||e=='\n')e=getchar();while(e!=' '&&e!='\n')s+=e,e=getchar();return s;}inline void swrite(string s){for(char e:s)putchar(e);printf("\n");}inline ll read() {ll x=0,y=1;char c=getchar();while(!isdigit(c)){if(c=='-')y=-1;c=getchar();}while(isdigit(c)){x=(x<<3)+(x<<1)+(c^48);c=getchar();}return x*=y;}inline void write(ll x) {if(x<0){x=-x,putchar('-');}ll sta[35],top=0;do sta[top++]=x%10,x/=10;while(x);while(top)putchar(sta[--top]+'0');}inline int max(int a,int b){if(a>b){return a;}return b;}inline int min(int a,int b){if(a>b){return b;}return a;}
}using namespace Lan;
int a[N];
int fa[N],index[V],num[V],val[N];//fa,该值的位置,大小,该位置的值
int L[B],R[B];//记录每个块的范围[l,r]
int ans[M];
int mx=-INF;
int lazy;//减法懒标记
struct Q{int op,l,r,x;
}que[M];
inline int find(int x){if(fa[x]==x){return x;}return fa[x]=find(fa[x]);
}
inline void merge(int x,int y){if(index[y]){//值存在fa[index[x]]=index[y];//合并}else{//不存在index[y]=index[x];val[index[x]]=y;//赋值为y}num[y]+=num[x];//合并index[x]=0;//清空num[x]=0;//清空
}
inline void rebuild(int pos){//记录最大值,合并值,处理值的数量 mx=-INF;lazy=0;for(int i=L[pos];i<=R[pos];i++){mx=max(mx,a[i]);if(!index[a[i]]){index[a[i]]=i;fa[i]=i;val[i]=a[i];}else{fa[i]=index[a[i]];}num[a[i]]++;}
}
inline void modify(int x){//区间 O(V)if((x<<1)<=(mx-lazy)){//x*2<=mx,for(int i=lazy;i<=x+lazy;i++){//a[i]<=x 都加x,lazy+x;O(x);if(index[i]){merge(i,i+x);}}lazy+=x;}else{//2*x>mxfor(int i=mx;i>x+lazy;i--){//a[i]>x 减去x,O(mx-x);if(index[i]){merge(i,i-x);}}//最大的值可能有x,与原本的mx取小mx=min(mx,x+lazy);}
}
inline int query(int l,int r,int x,int pos){int res=0;l=max(l,L[pos]);r=min(r,R[pos]);for(int i=l;i<=r;i++){if(val[find(i)]-lazy==x){res++;}}return res;
}
inline void update(int l,int r,int x,int pos){//下传lazyfor(int i=L[pos];i<=R[pos];i++){int temp=val[find(i)];a[i]=temp-lazy;index[temp]=0;num[temp]=0;}for(int i=L[pos];i<=R[pos];i++){val[i]=0;}l=max(l,L[pos]);r=min(r,R[pos]);//暴力操作for(int i=l;i<=r;i++){if(a[i]>x){ a[i]-=x;}}rebuild(pos);
}
inline void init(){mx=-INF;lazy=0;memset(num,0,sizeof(num));memset(index,0,sizeof(index));
}
inline bool inrange(int L,int R,int l,int r){//[l[L,R]r]return L>=l && R<=r;
}
inline bool outofrange(int L,int R,int l,int r){return L>r || l>R;
}
int main(){// ios::sync_with_stdio(false);// cin.tie(0),cout.tie(0);int n,m;n=read();m=read();for(int i=1;i<=n;i++){a[i]=read();}for(int i=1;i<=m;i++){que[i].op=read();que[i].l=read();que[i].r=read();que[i].x=read();}int blo=sqrt(n);int t=ceil(n*1.0/blo);for(int i=1;i<=t;i++){L[i]=(i-1)*t+1;R[i]=i*t;}//逐块处理for(int i=1;i<=t;i++){init();rebuild(i);for(int j=1;j<=m;j++){if(que[j].l>que[j].r){continue;}if(outofrange(L[i],R[i],que[j].l,que[j].r)){//不在这个区间continue;}if(que[j].op==1){if(inrange(L[i],R[i],que[j].l,que[j].r)){//询问区间包含这个块modify(que[j].x);//整块处理}else{update(que[j].l,que[j].r,que[j].x,i);//这一块处理完重构}}else{if(que[j].x+lazy>1e5+1){//没有贡献 continue;}if(inrange(L[i],R[i],que[j].l,que[j].r)){//询问区间包含这一块ans[j]+=num[que[j].x+lazy];}else{ans[j]+=query(que[j].l,que[j].r,que[j].x,i);//只能处理这一块的}}}}for(int i=1;i<=m;i++){if(que[i].op==2){write(ans[i]);putchar('\n');}}return 0;
}
不愧是大分块,lxl orz,还是刷刷简单点的分块题再来挑战ynoi吧
无期稿件P4119 [Ynoi2018] 未来日记
这篇关于P4117 [Ynoi2018] 五彩斑斓的世界的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!