【Leetcode】拓扑排序—课程表系列

本文主要是介绍【Leetcode】拓扑排序—课程表系列，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

有向无环图DAG图示：

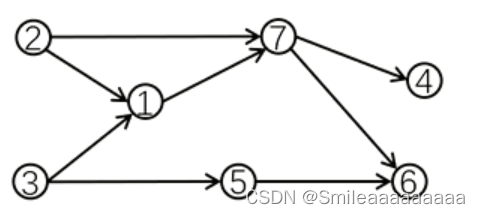
拓扑排序结果：{2,3,5,1,7,4,6}   {3,2,1,5,7,6,4}           不唯一

拓扑排序结果满足：对于图中的每条有向边(u,v)，u要排序在v之前；

应用：判断有向图中是否有环，可以生成拓扑序列；

Kahn（卡恩）算法

核心思想：用队列维护一个入度为0的节点的集合；

step1：一次遍历，统计所有节点的入度，并将所有入度为0的节点加入队列；

step2：从队列中取出一个节点u放入排序列表，并将节点u的全部有向边(u,vi)删除，删除过程中判断节点vi的入度是否为0，若为0则压入队列；

step3：直至队列为空时，若排序列表中的元素个数等于节点个数，则得到拓扑排序结果；

            若排序列表中的元素个数小于节点个数，则该图有环；

from collections import defaultdictclass GraphAdjacencyList:def __init__(self):self.graph = defaultdict(list)self.degree = {}self.sort = []def add_edge(self, start, end):  self.graph[start].append(end)if end not in self.graph:self.graph[end] = []def printsort(self):def init_du():for node in self.graph:self.degree[node] = 0for node, nxtnodes in self.graph.items():for nxtnode in nxtnodes:self.degree[nxtnode] += 1def topoSort():queue, self.sort = [], []for node, du in self.degree.items():if du == 0: queue.append(node)while queue:node = queue.pop(0)self.sort.append(node)for nxtnode in self.graph[node]:self.degree[nxtnode] -= 1if self.degree[nxtnode] == 0:queue.append(nxtnode)init_du()topoSort()  if len(self.graph) == len(self.sort): return self.sortelse: return -1if __name__ == "__main__":garph = [[2,1],[2,7],[1,7],[7,4],[7,6],[3,1],[3,5],[5,6]]DAG = GraphAdjacencyList()for i in range(len(garph)):DAG.add_edge(garph[i][0], garph[i][1])out = DAG.printsort()print(out)

变形：求字典序最小的拓扑序，将队列换成优先队列/小根堆；

例题

Leetcode 207 课程表

你这个学期必须选修 numCourses 门课程，记为 0 到 numCourses - 1 。

在选修某些课程之前需要一些先修课程。 先修课程按数组 prerequisites 给出，其中 prerequisites[i] = [ai, bi] ，表示如果要学习课程 ai 则 必须 先学习课程  bi 。例如，先修课程对 [0, 1] 表示：想要学习课程 0 ，你需要先完成课程 1 。请你判断是否可能完成所有课程的学习？如果可以，返回 true ；否则，返回 false 。

判断是否有环？     排序列表长度与图中结点数是否相等；

from collections import defaultdictclass Solution(object):def canFinish(self, numCourses, prerequisites):""":type numCourses: int:type prerequisites: List[List[int]]:rtype: bool"""tmp = defaultdict(list)                 # 邻接表for coarse in prerequisites:tmp[coarse[1]].append(coarse[0])degree = [0]*numCourses                 # 统计入度for coarse in prerequisites:degree[coarse[0]] += 1queue = []                              # 维护入度为0的队列for i in range(numCourses):if degree[i] == 0:queue.append(i)cnt = 0while queue:coarse = queue.pop(0)cnt += 1for nxtcoarse in tmp[coarse]:degree[nxtcoarse] -= 1if degree[nxtcoarse] == 0:queue.append(nxtcoarse)return cnt == numCourses# 生成邻接表和统计入度可合并操作

 Leetcode 210 课程表II

现在你总共有 numCourses 门课需要选，记为 0 到 numCourses - 1。给你一个数组 prerequisites ，其中 prerequisites[i] = [ai, bi] ，表示在选修课程 ai 前 必须 先选修 bi 。例如，想要学习课程 0 ，你需要先完成课程 1 ，我们用一个匹配来表示：[0,1] 。返回你为了学完所有课程所安排的学习顺序。可能会有多个正确的顺序，你只要返回 任意一种 就可以了。如果不可能完成所有课程，返回 一个空数组 。

输出拓扑排序或者空数组；

class Solution(object):def findOrder(self, numCourses, prerequisites):""":type numCourses: int:type prerequisites: List[List[int]]:rtype: List[int]"""degree = [0]*numCourses    tmp = defaultdict(list)   queue = deque()for cur, pre in prerequisites:degree[cur] += 1                      tmp[pre].append(cur)                 for i in range(numCourses):if degree[i] == 0: queue.append(i)    out, cnt = [], 0while queue:course = queue.popleft()out.append(course)cnt += 1for i in tmp[course]:                degree[i] -= 1if degree[i] == 0:               queue.append(i)  return out if cnt == numCourses else []

  Leetcode 1462 课程表IV

你总共需要上 numCourses 门课，课程编号依次为 0 到 numCourses-1 。你会得到一个数组 prerequisite ，其中 prerequisites[i] = [ai, bi] 表示如果你想选 bi 课程，你 必须 先选 ai 课程。有的课会有直接的先修课程，比如如果想上课程 1 ，你必须先上课程 0 ，那么会以 [0,1] 数对的形式给出先修课程数对。先决条件也可以是 间接 的。如果课程 a 是课程 b 的先决条件，课程 b 是课程 c 的先决条件，那么课程 a 就是课程 c 的先决条件。你也得到一个数组 queries ，其中 queries[j] = [uj, vj]。对于第 j 个查询，您应该回答课程 uj 是否是课程 vj 的先决条件。返回一个布尔数组 answer ，其中 answer[j] 是第 j 个查询的答案。

前两题构建的tmp都是根据前置课程找当前课程，而这道题需要根据当前课程找前置课程；

方法一：从前置课程数量少的开始更新untmp；

以 tmp={2:4; 0:1,2; 1:2;} 为例：

构造untmp[4]时除了需要添加2，还需要添加2的前置课程untmp[2]；

构造untmp[2]时除了需要添加0和1，还需要添加0和1的前置课程untmp[0]，untmp[1]；

untmp[0]无前置课程，untmp[1]的前置课程为0；

所以需要按照untmp[0]-untmp[1]-untmp[2]-untmp[4]的顺序构造，即拓扑排序顺序；

class Solution(object):def checkIfPrerequisite(self, numCourses, prerequisites, queries):""":type numCourses: int:type prerequisites: List[List[int]]:type queries: List[List[int]]:rtype: List[bool]"""degree = [0]*numCourses   tmp = defaultdict(set)untmp =  defaultdict(set) for pre, cur in prerequisites:        degree[cur] += 1                tmp[pre].add(cur) queue = []for i in range(numCourses):if degree[i] == 0: queue.append(i)    while queue:pre = queue.pop(0)for cur in tmp[pre]:untmp[cur].add(pre)untmp[cur] = untmp[cur] | untmp[pre] # 用set可自动去重，也方便查找degree[cur] -= 1if degree[cur] == 0:queue.append(cur)out = [False]*len(queries)for i, query in enumerate(queries):if query[1] in untmp and query[0] in untmp[query[1]]: out[i] = Truereturn out

方法二：记忆化搜索，在构造untmp[4]的过程中将untmp[2]、untmp[1]、untmp[0]都保存，这样按tmp顺序构造untmp[2]/untmp[1]/untmp[0]时直接读取即可；

class Solution(object):def checkIfPrerequisite(self, numCourses, prerequisites, queries):""":type numCourses: int:type prerequisites: List[List[int]]:type queries: List[List[int]]:rtype: List[bool]"""tmp = defaultdict(list)   for pre, cur in prerequisites:                      tmp[pre].append(cur)memo = {}def helper(pre, cur):if (pre, cur) in memo: return memo[(pre, cur)]memo[(pre, cur)] = Falseif cur in tmp[pre]:memo[(pre, cur)] = Trueelse:for nxt in tmp[pre]:if helper(nxt, cur):memo[(pre, cur)] = Truebreakreturn memo[(pre, cur)]out = [False]*len(queries)for i, query in enumerate(queries):out[i] = helper(query[0], query[1])return out

这篇关于【Leetcode】拓扑排序—课程表系列的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---