求最大公约数及Hankson趣味题

本文主要是介绍求最大公约数及Hankson趣味题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、问题说明

基础：
求N个数的最大公约数和最大公倍数。
提高：
Hanks博士是BT（Bio-Tech，生物技术）领域的知名专家，他的儿子名叫Hankson。现在，刚刚放学回家的Hankson正在思考一个有趣的问题。
今天在课堂上，老师讲解了如何求两个正整数c1和c2的最大公约数和最小公倍数。现在Hankson认为自己已经熟练地掌握了这些知识，他开始思考一个“求公约数”和“求公倍数”之类问题的“逆问题”，这个问题是这样的：已知正整数a0,a1,b0,b1，设某未知正整数x满足：
1、 x和a0的最大公约数是a1；
2、 x和b0的最小公倍数是b1。
Hankson的“逆问题”就是求出满足条件的正整数x。但稍加思索之后，他发现这样的x并不唯一，甚至可能不存在。因此他转而开始考虑如何求解满足条件的x的个数。请你帮助他编程求解这个问题。
输入格式
输入第一行为一个正整数n，表示有n组输入数据。接下来的n行每行一组输入数据，为四个正整数a0，a1，b0，b1，每两个整数之间用一个空格隔开。输入数据保证a0能被a1整除，b1能被b0整除。
输出格式
输出共n行。每组输入数据的输出结果占一行，为一个整数。
对于每组数据：若不存在这样的x，请输出0；若存在这样的x，请输出满足条件的x的个数；
样例输入
2
41 1 96 288
95 1 37 1776
样例输出
6
2

二、分析

1、基础

用一数组a[]存储输入的N个数，先用gcd()求两个数的最大公约数，然后求a[1]=gcd(a[0],a[1])，再求a[2]=gcd(a[1],a[2])，依次下去，最后a[N-1]既是结果。最小公倍数则调用lcm()。

2、提高

已知
gcd(x,a0)=a1……①
lcm(x,b0)=b1;
根据两个数的最大公约数和最小公倍数的关系，mn/gcd(m,n)=lcm(m,n);
转化得，gcd(x,b0)=xb0/b1……②
由①②根据最大公约数的性质得，
gcd(x/a1,a0/a1)=1……③
gcd(b1/b0,b1/x)=1……④
符合条件的x必然满足③式和④式，故枚举b1的因子且满足③、④式就是x。
算法流程图

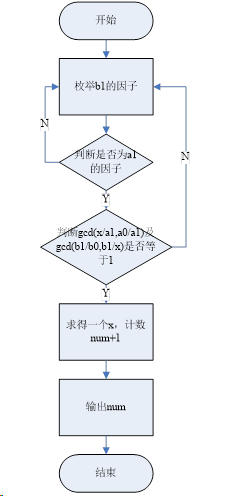
三、运行结果

1、基础

2、提高

四、程序实现

1、N个数的最大公约数

* 名称：第二次作业
* 文件名：基础.cpp
* 说明：多个数的最大公约数及最小公倍数
*/
#include"iostream"
using namespace std;//求最大公约数
int gcd(int a,int b)
{int ans = 1;//储存第一步中约掉的若干个2int gcd;//储存最终返回的结果 while (a % 2 == 0 && b % 2 == 0)//如果a，b均为偶数则用2约简 {a /= 2;b /= 2;ans *= 2;}while (a != b)//判断两数是否相等，相等则得出最大约数{if (a > b)a -= b;//以较大的数减较小的数elseb -= a;//以较大的数减较小的数}gcd = a * ans; //求第一步中约掉的若干个2与第二步中等数的乘积 return gcd;
}//求最小公倍数
int lcm(int a, int b) {return(a*b / gcd(a, b));
}int main() {int a[1000];int temp1, temp2;int i = 0;cin >> i;//输入需要几个数for (int j = 0; j < i; j++) {cin >> a[j];}for (int k = 0; k < i - 1; k++) {temp1 = a[0];temp1 = gcd(temp1, a[k + 1]);}for (int k = 0; k < i - 1; k++) {temp2 = a[0];temp2 = lcm(temp2, a[k + 1]);}int gcd = temp1;cout << "最大公约数 " << temp1 << endl;int lcm = temp2;cout << "最小公倍数 " << temp2 << endl;system("pause");
}

2、Hankson问题

*	名  称：第二次作业
*	文件名：homework2.cpp
*	说  明：Hankson问题实现
*/#include"iostream"
using namespace std;//求最大公约数
int gcd(int a, int b) 
{int ans = 1;//储存第一步中约掉的若干个2int gcd;//储存最终返回的结果 while (a % 2 == 0 && b % 2 == 0)//如果a，b均为偶数则用2约简 {a /= 2;b /= 2;ans *= 2;}while (a != b)//判断两数是否相等，相等则得出最大约数{if (a > b)a -= b;//以较大的数减较小的数elseb -= a;//以较大的数减较小的数}gcd = a * ans; //求第一步中约掉的若干个2与第二步中等数的乘积 return gcd;
}int main() {int n;//n组数据cin >> n;int a0, a1, b0, b1;//正整数a0,a1,b0,b1for (int i = 1; i <= n;i++) {int num = 0;cin >> a0 >> a1 >> b0 >> b1;//	枚举b1的因子，判定条件为j*j<=b1,防止重复记录同一个因子for (int j = 1; j*j <= b1; j++) {if (b1%j == 0) {int x = j;if (x%a1 == 0)//判断最大公约数是否为1if (gcd(x / a1, a0 / a1) == 1 && gcd(b1 / b0, b1 / x) == 1)num++;x = b1 / x;if(x != j && x % a1 == 0)if (gcd(x / a1, a0 / a1) == 1 && gcd(b1 / b0, b1 / x) == 1)num++;}}cout << num << endl;}system("pause");return 0;
}

五、个人总结

数学的学习与算法的设计是紧密结合的，本次作业中核心的就在于对最大公约数的数学知识的充分了解，并且结合计算机的优势，可以不断循环计算。两者结合能够很有效的解决一些问题。

这篇关于求最大公约数及Hankson趣味题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---