《学一辈子光线追踪》 五 产生随机方向

2024-04-07 20:38
文章标签 方向 产生 随机 一辈子 追踪 光线

本文主要是介绍《学一辈子光线追踪》 五 产生随机方向，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

蒙特卡洛光线追踪技术系列 见 蒙特卡洛光线追踪技术

这一节结束后，我会对前面的关于概率和光线追踪的知识进行一下总结和归纳。

在本章和下两章中，让我们加强理解和工具，找出哪个康奈尔盒子的渲染结果是正确的。我们先来看看如何生成随机方向，但为了简化，我们假设z轴是曲面法向，theta是与法向的夹角。我们将在下一章中把它们定向到曲面法向量。我们只讨论关于z的旋转对称分布，所以p(direction) = f(theta)。如果你有学过高级微积分，你可能记得在球坐标系的球面上 dA = sin(theta)*dtheta*dphi 。如果你没有，下一步你必须遵守我说的，但当你学习过高级微积分时你会得到它。

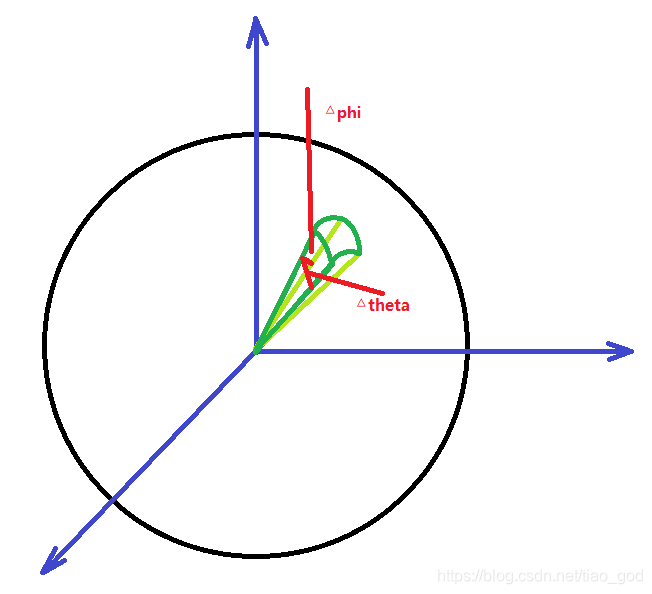
给定球面上的方向pdf，p(direction) = f(theta)，theta和phi上的一维pdf为：

a(phi) = 1/(2Pi)  (是uniform的)
b(theta) = 2*Pi*f(theta)sin(theta) （说明竖直方向的pdf与sin(theta)相关）

对于均匀随机数r1和r2，第2章中介绍的材料得到：

r1 = INTEGRAL_0^phi (1/(2*Pi)) = phi/(2*Pi)

即 ：\int_{0}^{phi} (1/(2*Pi))

解 phi 我们得到：

phi = 2*Pi*r1

对theta 我们有：

r2 = INTEGRAL_0^theta 2*Pi*f(t)sin(t)

即 ：\int_{0}^{theta} (2*Pi*f(t)*sin(t))

这里，t是一个伪变量。让我们为f() 尝试一些不同的函数。

一、让我们先在球体上尝试均匀的密度。单位球的面积是4Pi，因此单位球上的均匀 p(direction) = 1/(4Pi)。f(theta)=p(direction)，代进去计算得：

r2 = -cos(theta)/2 - (-cos(0)/2)= (1 - cos(theta))/2

解 cos(theta) 得到：

cos(theta) = 1 - 2*r2

我们不为theta求解，因为我们可能只需要知道cos(theta)，也不希望不必要的 acos() 调用到处运行。

要生成朝向 (θ，phi) 的单位矢量方向，我们将其转换为笛卡尔坐标：

x = cos(phi)*sin(theta)
y = sin(phi)*sin(theta)
z = cos(theta)

利用cos^2+sin^2=1的恒等式，我们得到以下随机项 (r1,r2):

x = cos(2*Pi*r1)*sqrt(1 - (1-2*r2)^2)
y = sin(2*Pi*r1)*sqrt(1 - (1-2*r2)^2)
z = 1 - 2*r2

简化一点，(1-2*r2)^2 = 1 - 4*r2 + 4*r2^2，所以：

x = cos(2*Pi*r1)*2*sqrt(r2*(1-r2))
y = sin(2*Pi*r1)*2*sqrt(r2*(1-r2))
z = 1 - 2*r2

我们可以输出来显示。为了方便这里就用OpenGL来进行显示：

#include <stdlib.h>
/*Note that the __glut*WithExit routines should NEVER be called directly.
To avoid the atexit workaround, #define GLUT_DISABLE_ATEXIT_HACK.*/
#define GLUT_DISABLE_ATEXIT_HACK
#include "glut.h"#include<gl/glu.h>
#include<gl/gl.h>#include "vec3.h"
#define WIDTH 500
#define HEIGHT 500
#include <math.h>
#include <stdlib.h>
#include <stdio.h>
#include "time.h"
#define M_PI 3.14159265
GLfloat viewR = 8.0;  //曾经的
float x_k = 1, y_k = 1;//因为坐标轴可能反转，所以设置一个系数。
float upValue = 1.0;
GLuint mainw, subw1;
float OrthoLength = 5.0;
float x_y_cor = 45;
float z_cor = 45;
int flag = 0; //判断是否按下的flag
static int current_Dot[2] = { 0, 0 };
float dx, dy;double myRandom() {return rand() / (RAND_MAX + 1.0);
}void display(void) {glClearColor(1.0f, 1.0f, 1.0f, 0.0f);glLineWidth(1.0);glMatrixMode(GL_PROJECTION);glLoadIdentity();//glOrtho(-OrthoLength, OrthoLength, -OrthoLength*((double)screenheight/(double)screenwidth)//, OrthoLength*((double)screenheight / (double)screenwidth), 0.1, 100);  //把世界坐标宽6.0高6.0的世界放入视口中。gluPerspective(45, (double)HEIGHT / (double)WIDTH, 0.1, 100);glMatrixMode(GL_MODELVIEW);glLoadIdentity();//第二个是z     gluLookAt(x_k*viewR * cos(z_cor*M_PI / 180)*cos(x_y_cor*M_PI / 180), viewR * sin(z_cor*M_PI / 180),y_k*viewR * cos(z_cor*M_PI / 180)* sin(x_y_cor*M_PI / 180), 0.0, 0.0, 0.0, 0.0, upValue, 0.0);//第一个是 两箭头 第二个是 一箭头  第三个是 三箭头glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);glColor3d(1.0, 0, 0);glutSwapBuffers();
}
void myMouse(int button, int state, int x, int y) {if (state == GLUT_DOWN){if (button == GLUT_LEFT_BUTTON){flag = 1;current_Dot[0] = x; current_Dot[1] = HEIGHT - y;}}else if (state == GLUT_UP) {if (button == GLUT_LEFT_BUTTON) {flag = 0;}}
}void myMovedMouse(int x, int y) {if (flag == 1){dy = HEIGHT - y - current_Dot[1];dx = x - current_Dot[0];z_cor = z_cor - dy / 3;if (z_cor<-360) {z_cor = z_cor + 360;}else if (z_cor > 360) {z_cor = z_cor - 360;}if ((z_cor > 90 && z_cor<270) | (z_cor<-90 && z_cor>-270)) {upValue = -1.0;}else {upValue = 1.0;}x_y_cor = x_y_cor + dx / 3;if (x_y_cor > 360) {x_y_cor = x_y_cor - 360;}else if (x_y_cor < -360) {x_y_cor = x_y_cor + 360;}current_Dot[0] = x;current_Dot[1] = HEIGHT - y;display();}}
void reShape(int width, int height) {glViewport(0, 0, width, height);
}
int main(int argc,char **argv) {glutInit(&argc, argv);glutInitDisplayMode(GLUT_DOUBLE | GLUT_RGB);glutInitWindowSize(WIDTH, HEIGHT);glutInitWindowPosition(150, 100);glutCreateWindow("Feimos");glViewport(0, 0, WIDTH, HEIGHT);glEnable(GL_DEPTH_TEST);glutDisplayFunc(display);glutReshapeFunc(reShape);glutMouseFunc(myMouse);glutMotionFunc(myMovedMouse);glutMainLoop();
}

先把可以进行转动的框架打好，然后开始往里面写数据：

	srand(time(NULL));for (int i = 0;i < N;i++) {float r1 = myRandom();float r2 = myRandom();float x = cos(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));float y = sin(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));float z = 1 - 2 * r2;myRandomPoint[i].e[0] = x;myRandomPoint[i].e[1] = y;myRandomPoint[i].e[2] = z;}

并进行显示：

	for (int i = 0;i < N;i++) {glPushMatrix();glTranslatef(myRandomPoint[i].e[0], myRandomPoint[i].e[1], myRandomPoint[i].e[2]);glutWireSphere(0.02, 20, 20);glPopMatrix();//弹出现在的栈}

可以得到图：

可以看到分布挺均匀的（在程序里可以360度转动）。

二、现在让我们推导半球上的一致性。半球上的密度均匀意味着 p(direction) = 1/(2*Pi) ，仅仅改变θ方程中的常数，就会得到：

cos(theta) = 1 - r2

令人欣慰的是cos(theta) 将从1变为0，因此theta将从0变为Pi/2。与其绘制它，不如对已知解进行二维积分。让我们在半球上积分余弦立方（用已知解任意选取）。首先让我们用手来做：

INTEGRAL cos^3 = 2*Pi*INTEGRAL_0^PI/2 cos^3 sin = PI/2.

现在积分重要性抽样。p(direction) = 1/(2*Pi)，所以我们平均 f/p 为 cos^3/ (1/(2*Pi)) ，我们可以测试：

		x = cos(2 * M_PI * r1) * 2 * sqrt(r2 * (1 - r2));y = sin(2 * M_PI * r1) * 2 * sqrt(r2 * (1 - r2));z = 1 - r2;sum += (z*z*z) / (1.0 / (2.0*M_PI));

得到结果：

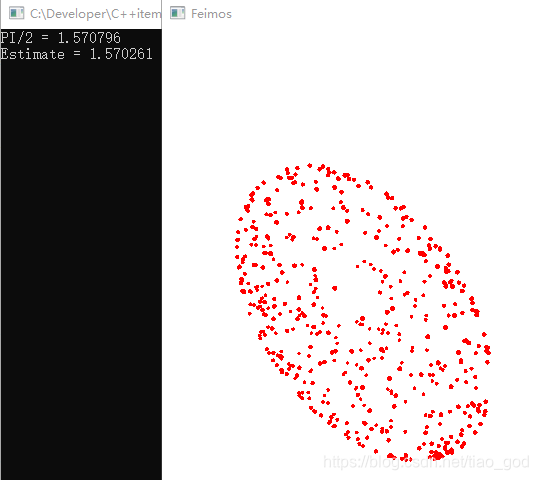
三、为了检验一下之前的结果，再测试一下lambertian物体的pdf：

p(direction) = cos(theta) / Pi

r2 = INTEGRAL_0^theta 2*Pi*cos(t)/Pi * sint dt = (-cos^2 t)|0-theta  = 1 - cos^2(theta)

cos(theta) = sqrt(1-r2)

所以:

x = cos(2*Pi*r1)*sqrt(r2)

y = sin(2*Pi*r1)*sqrt(r2)

z = sqrt(1-r2)

	float sum = 0.0;for (int i = 0;i < N;i++) {float r1 = myRandom();float r2 = myRandom();//float x = cos(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));//float y = sin(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));//float z = 1 - 2 * r2;float x = cos(2 * M_PI*r1) * sqrt(r2);float y = sin(2 * M_PI*r1) * sqrt(r2);float z = sqrt(1 - r2);//float x = cos(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));//float y = sin(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));//float z = 1 - r2;myRandomPoint[i].e[0] = x;myRandomPoint[i].e[1] = y;myRandomPoint[i].e[2] = z;//sum += (z*z*z) / (1.0 / (2.0*M_PI));sum += (z*z*z) / (z / (M_PI));}

得到结果：

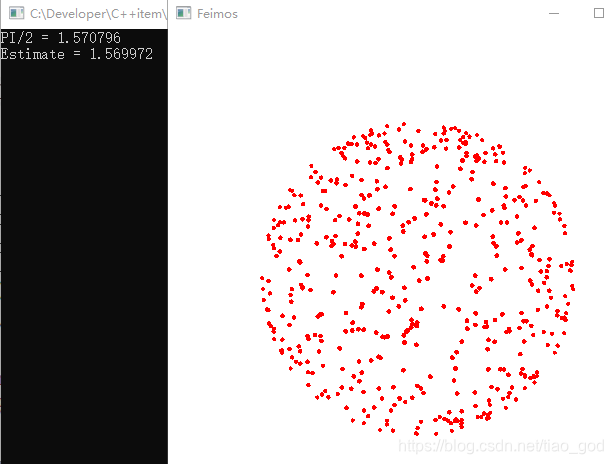
很明显，越靠近球体上方的密度越大。

根据计算，模拟半球比p(direction)=cos(theta)/Pi的效果要好。？？感觉，不大对啊，于情于理感觉都是cos(theta)/Pi更好啊。

我又对比运行了好几次，都是模拟半球更好，突然发现自己有个地方写错了：

        double x = cos(2 * M_PI*r1) * 2 * sqrt(r2);
        double y = sin(2 * M_PI*r1) * 2 * sqrt(r2);

应该中间乘2。我重新写了个完整的代码：

	double sum1 = 0.0;double sum2 = 0.0;for (int i = 0;i < N;i++) {double r1 = myRandom();double r2 = myRandom();//float x = cos(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));//float y = sin(2 * M_PI*r1) * 2 * sqrt(r2*(1 - r2));//float z = 1 - 2 * r2;//p(directions) = cos(theta) / Pidouble x = cos(2 * M_PI*r1) * 2 * sqrt(r2);double y = sin(2 * M_PI*r1) * 2 * sqrt(r2);double z = sqrt(1 - r2);sum1 += (z*z*z) / (z / (M_PI));// p(direction) = 1/(2*Pi)x = cos(2 * M_PI * r1) * 2 * sqrt(r2 * (1 - r2));y = sin(2 * M_PI * r1) * 2 * sqrt(r2 * (1 - r2));z = 1 - r2;sum2 += (z*z*z) / (1.0 / (2.0*M_PI));myRandomPoint[i].e[0] = x;myRandomPoint[i].e[1] = y;myRandomPoint[i].e[2] = z;}printf("PI/2 = %lf\n",M_PI/2);printf("Estimate = %lf\n", sum1/N);printf("Difference = %lf\n",(sum1/N-M_PI/2));printf("PI/2 = %lf\n", M_PI / 2);printf("Estimate = %lf\n", sum2 / N);printf("Difference = %lf\n", (sum2 / N - M_PI / 2));

得到最终结果：

可以证实 cos(theta)/Pi预测更好一些。

这篇关于《学一辈子光线追踪》 五 产生随机方向的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/883617。

相关文章

SpringBoot如何使用TraceId日志链路追踪

SpringBoot如何使用TraceId日志链路追踪

《SpringBoot如何使用TraceId日志链路追踪》文章介绍了如何使用TraceId进行日志链路追踪,通过在日志中添加TraceId关键字,可以将同一次业务调用链上的日志串起来,本文通过实例代码... 目录项目场景：实现步骤1、pom.XML 依赖2、整合logback，打印日志，logback-sp
阅读更多...
Python中的随机森林算法与实战

Python中的随机森林算法与实战

《Python中的随机森林算法与实战》本文详细介绍了随机森林算法,包括其原理、实现步骤、分类和回归案例,并讨论了其优点和缺点,通过面向对象编程实现了一个简单的随机森林模型,并应用于鸢尾花分类和波士顿房... 目录1、随机森林算法概述2、随机森林的原理3、实现步骤4、分类案例：使用随机森林预测鸢尾花品种4.1
阅读更多...
使用C#如何创建人名或其他物体随机分组

使用C#如何创建人名或其他物体随机分组

《使用C#如何创建人名或其他物体随机分组》文章描述了一个随机分配人员到多个团队的代码示例,包括将人员列表随机化并根据组数分配到不同组,最后按组号排序显示结果... 目录C#创建人名或其他物体随机分组此示例使用以下代码将人员分配到组代码首先将lstPeople ListBox总结C#创建人名或其他物体随机分组
阅读更多...
MCU7.keil中build产生的hex文件解读

MCU7.keil中build产生的hex文件解读

1.hex文件大致解读 闲来无事,查看了MCU6.用keil新建项目的hex文件 用FlexHex打开 给我的第一印象是:经过软件的解释之后,发现这些数据排列地十分整齐 :02000F0080FE71:03000000020003F8:0C000300787FE4F6D8FD75810702000F3D:00000001FF 把解释后的数据当作十六进制来观察 1.每一行数据
阅读更多...
嵌入式方向的毕业生，找工作很迷茫

嵌入式方向的毕业生，找工作很迷茫

一个应届硕士生的问题： 虽然我明白想成为技术大牛需要日积月累的磨练，但我总感觉自己学习方法或者哪些方面有问题，时间一天天过去，自己也每天不停学习，但总感觉自己没有想象中那样进步，总感觉找不到一个很清晰的学习规划……眼看 9 月份就要参加秋招了，我想毕业了去大城市磨练几年，涨涨见识，拓开眼界多学点东西。但是感觉自己的实力还是很不够，内心慌得不行，总怕浪费了这人生唯一的校招机会，当然我也明白，毕业
阅读更多...
理解分类器（linear）为什么可以做语义方向的指导？（解纠缠）

理解分类器（linear）为什么可以做语义方向的指导？（解纠缠）

Attribute Manipulation（属性编辑）、disentanglement（解纠缠）常用的两种做法：线性探针和PCA_disentanglement和alignment-CSDN博客 在解纠缠的过程中，有一种非常简单的方法来引导G向某个方向进行生成，然后我们通过向不同的方向进行行走，那么就会得到这个属性上的图像。那么你利用多个方向进行生成，便得到了各种方向的图像，每个方向对应了很多
阅读更多...
AI学习指南深度学习篇-带动量的随机梯度下降法的基本原理

AI学习指南深度学习篇-带动量的随机梯度下降法的基本原理

AI学习指南深度学习篇——带动量的随机梯度下降法的基本原理 引言 在深度学习中，优化算法被广泛应用于训练神经网络模型。随机梯度下降法（SGD）是最常用的优化算法之一，但单独使用SGD在收敛速度和稳定性方面存在一些问题。为了应对这些挑战，动量法应运而生。本文将详细介绍动量法的原理，包括动量的概念、指数加权移动平均、参数更新等内容，最后通过实际示例展示动量如何帮助SGD在参数更新过程中平稳地前进。
阅读更多...
随机密码生成器应具备哪些默认功能？

随机密码生成器应具备哪些默认功能？

阅读更多...
AI学习指南深度学习篇-带动量的随机梯度下降法简介

AI学习指南深度学习篇-带动量的随机梯度下降法简介

AI学习指南深度学习篇 - 带动量的随机梯度下降法简介 引言 在深度学习的广阔领域中，优化算法扮演着至关重要的角色。它们不仅决定了模型训练的效率，还直接影响到模型的最终表现之一。随着神经网络模型的不断深化和复杂化，传统的优化算法在许多领域逐渐暴露出其不足之处。带动量的随机梯度下降法（Momentum SGD）应运而生，并被广泛应用于各类深度学习模型中。 在本篇文章中，我们将深入探讨带动量的随
阅读更多...
[SWPUCTF 2021 新生赛]web方向(一到六题) 解题思路，实操解析，解题软件使用，解题方法教程

[SWPUCTF 2021 新生赛]web方向(一到六题) 解题思路，实操解析，解题软件使用，解题方法教程

题目来源 NSSCTF | 在线CTF平台因为热爱，所以长远！NSSCTF平台秉承着开放、自由、共享的精神，欢迎每一个CTFer使用。https://www.nssctf.cn/problem   [SWPUCTF 2021 新生赛]gift_F12 这个题目简单打开后是一个网页  我们一般按F12或者是右键查看源代码。接着我们点击ctrl+f后快速查找，根据题目给的格式我们搜索c
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2