本文主要是介绍【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
22. 括号生成
数字
n代表生成括号的对数,请你设计一个函数,用于能够生成所有可能的并且 有效的 括号组合。示例 1:
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
示例 2:
输入:n = 1 输出:["()"]
提示:
1 <= n <= 8
【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树
定义dfs递归函数,将叶子节点填充到ret中。
定义 ret 记录结果。
定义path表示树节点。
定义left,right表示当前树节点的左右括号数量。用来正确进入到下一个子树中。
任何情况下 left>=right必须满足才是有效的形式。
如果需要添加左括号,left<=n,left+1<=n,left<n。
如果需要添加右括号,left>=right,left>=right+1,left>right。
以上是正确进入子树的规则。
递归函数dfs内部逻辑,将path树所有叶子节点填充到ret,相当于将左子树叶子节点填充到ret,右子树叶子节点填充到ret。
if (left < n) { path.push_back('('); left++; dfs(); path.pop_back(); left--; }
这一整个代码表示左子树递归。因为是模拟树所以必须时时刻刻维护path,left,right的定义。因为这些变量都与树的定义有关。
if (left > right) { path.push_back(')'); right++; dfs(); path.pop_back(); right--; }
这一整个代码表示右子树递归。因为是模拟树所以必须时时刻刻维护path,left,right的定义。因为这些变量都与树的定义有关。
递归函数的出口,当path.size() == 2 * n,此时是叶子节点,将path添加到ret中。
class Solution {
public:int left, right;string path;vector<string> ret;int n;vector<string> generateParenthesis(int _n) {n = _n;dfs();return ret;}void dfs() {if (path.size() == 2 * n) {ret.push_back(path);return;}if (left < n) {path.push_back('(');left++;dfs();path.pop_back();left--;}if (left > right) {path.push_back(')');right++;dfs();path.pop_back();right--;}}
};77. 组合
给定两个整数
n和k,返回范围[1, n]中所有可能的k个数的组合。你可以按 任何顺序 返回答案。
示例 1:
输入:n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4], ]
示例 2:
输入:n = 1, k = 1 输出:[[1]]
提示:
1 <= n <= 20
1 <= k <= n
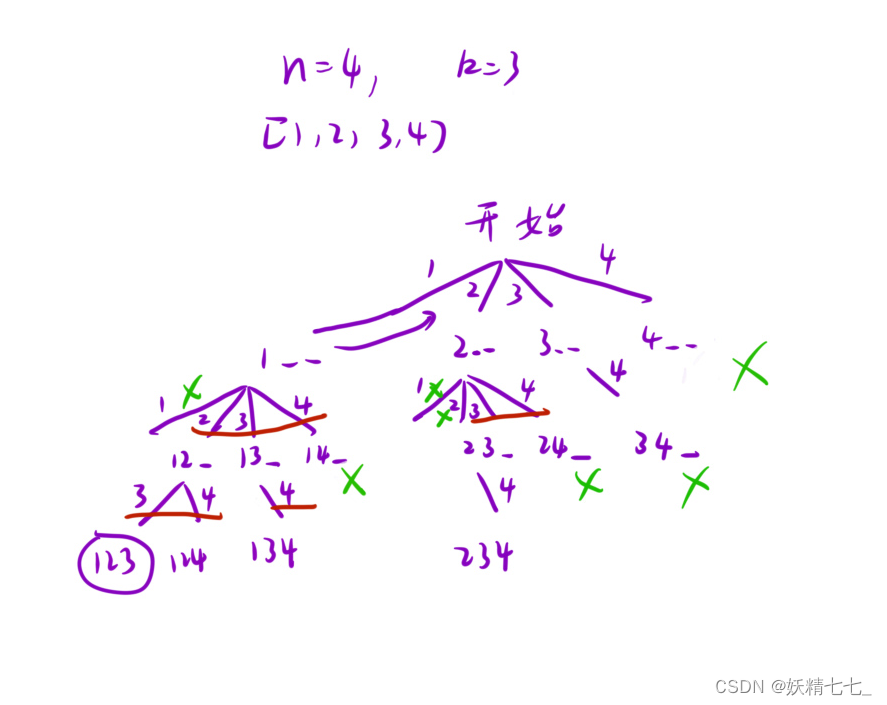
定义dfs递归函数,将path树叶子节点填充到ret中。
思考模拟树需要定义的变量。
定义path表示树的根节点。
定义pos表示子树开始遍历的下标。
定义ret记录结果。
小技巧,将n和k定义成全局变量,就不用每次都传入递归函数中。
递归函数的内部逻辑,将所有子树的叶子节点填充到 ret 中。
for (int i = pos; i <= n; i++) { path.push_back(i); int temp = pos; pos = i + 1; dfs(); path.pop_back(); pos = temp; }
for 循环中的所有代码表示一个子树的递归,用for循环变量所有的子树。
遍历下一个子树的时候,需要维护path和pos的定义。因为是模拟树所以必须时时刻刻维护path,pos的定义。因为这些变量都与树的定义有关。
递归出口,当path.size() == k时,表示是叶子节点,此时将path填充到ret中。
class Solution {
public:vector<vector<int>> ret;vector<int> path;int pos = 1;int n, k;vector<vector<int>> combine(int _n, int _k) {n = _n;k = _k;dfs();return ret;}void dfs() {if (path.size() == k) {ret.push_back(path);return;}for (int i = pos; i <= n; i++) {path.push_back(i);int temp = pos;pos = i + 1;dfs();path.pop_back();pos = temp;}}
};494. 目标和
给你一个非负整数数组
nums和一个整数target。向数组中的每个整数前添加
'+'或'-',然后串联起所有整数,可以构造一个 表达式 :
例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。返回可以通过上述方法构造的、运算结果等于
target的不同 表达式 的数目。示例 1:
输入:nums = [1,1,1,1,1], target = 3 输出:5 解释:一共有 5 种方法让最终目标和为 3 。 -1 + 1 + 1 + 1 + 1 = 3 +1 - 1 + 1 + 1 + 1 = 3 +1 + 1 - 1 + 1 + 1 = 3 +1 + 1 + 1 - 1 + 1 = 3 +1 + 1 + 1 + 1 - 1 = 3
示例 2:
输入:nums = [1], target = 1 输出:1
提示:
1 <= nums.length <= 20
0 <= nums[i] <= 1000
0 <= sum(nums[i]) <= 1000
-1000 <= target <= 1000
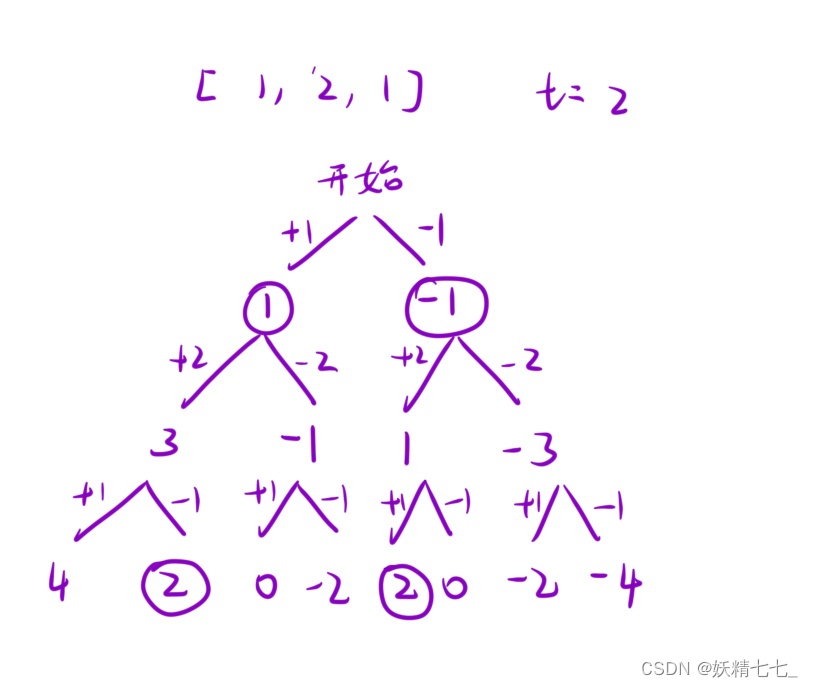
定义dfs将树叶子节点符合要求的计数。
定义path表示树根节点。
定义pos表示nums下一个应该遍历下标,也就是子树的可能性。
上面的定义模拟树。
定义ret记录结果。
定义target表示目标和,定义为全局变量。
递归函数dfs内部逻辑,将左子树叶子节点符合要求的计数,将右子树叶子节点符合要求的计数。
递归左右子树的时候需要时时刻刻维护path和pos。
path += nums[pos]; pos++; dfs(nums); pos--; path -= nums[pos];
递归左子树。因为是模拟树所以必须时时刻刻维护path,pos的定义。因为这些变量都与树的定义有关。
path -= nums[pos]; pos++; dfs(nums); pos--; path += nums[pos];
递归右子树。因为是模拟树所以必须时时刻刻维护path,pos的定义。因为这些变量都与树的定义有关。
递归函数的出口,当pos == nums.size()表示是叶子节点,同时path==target表示是符合要求的情况,此时ret++。
class Solution {
public:int ret;int path;int pos;int target;int findTargetSumWays(vector<int>& nums, int _target) {target=_target;dfs(nums);return ret;}void dfs(vector<int>& nums) {if (pos == nums.size()) {if (path == target)ret++;return;}path += nums[pos];pos++;dfs(nums);pos--;path -= nums[pos];path -= nums[pos];pos++;dfs(nums);pos--;path += nums[pos];}
};利用临时变量的性质自动维护树的定义。
此时就不需要手动维护树的定义。
手动维护树的定义需要进行操作,此时临时变量空间仅仅是int类型的,所以相对于手动维护,时间会快一点。
如果临时变量是vector类型效率可能会减低,因为每次都需要开辟vector的空间。此时用全局变量手动维护可能会更好一点。
int 类型可以不使用全局变量,利用临时变量自动维护,此时效率可能会变快。因为加减操作也是需要时间的。
class Solution {
public:int ret;int target;int findTargetSumWays(vector<int>& nums, int _target) {target = _target;dfs(nums, 0, 0);return ret;}void dfs(vector<int>& nums, int pos, int path) {if (pos == nums.size()) {if (path == target)ret++;return;}dfs(nums, pos + 1, path + nums[pos]);dfs(nums, pos + 1, path - nums[pos]);}
};结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
这篇关于【三十五】【算法分析与设计】综合练习(2),22。 括号生成,77。 组合,494。 目标和,模拟树递归,临时变量自动维护树定义,递归回溯,非树结构模拟树的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






