蓝桥杯2013年第四届真题-格子刷油漆

本文主要是介绍蓝桥杯2013年第四届真题-格子刷油漆，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

在这里插入图片描述

思路：
对于题目给出的几个行走规则，走的方式有很多；但是以某个格子为出发点的方式固定。

将整个矩形刷完，我们的起点主要分为以下两大类：
1.从四个顶点之一出发
2.从中间某个点出发

1.从四个顶点之一出发

①第一步走同一列的另一个格子，然后再走下一列。接着重复这个过程。如下图所示：
在这里插入图片描述
假设从顶点A出发，那么第一步没得选，只能走向B；接着在B点时，此时就有两种选择方案，要么走向C，要么走向D。假设走向了D，那么此时D点就只能选C，接着在C点时，其又可以选择E或F……然后重复上面这个过程，直到最终走到矩形的另一侧

这种情况下，我们用a[i] 来表示一个2x i 的矩形从一个顶点出发，要按规则走完全部格数的方案数。

a[i]=a[i-1]*2;

②第一步走下一列，之后也还是不断地走下一列，当最终走到最后一列后再返回。返回时，由于格子的高度为2，那么在返回时，路径唯一，如下图所示：
在这里插入图片描述
假设从顶点A出发，那么第一步可以选C或D共两种方案，假设选的是C，那么接下来又可以选择E或F……当最后到了最后一列，比如到了I，那么此时返回的路线也就唯一确定了
我们用b[i] 表示从一个顶点出发最后到达他的相对位置的方案种数为多少

于是得到状态转移方程：b[ i ]=2×b[ i-1] （乘2的原因是每次都有两种选择，如在A点可选C或D）

③第一步走另一列,再由该列返回前一列，然后再从前一列走向另一列的另一个格子，如下图所示

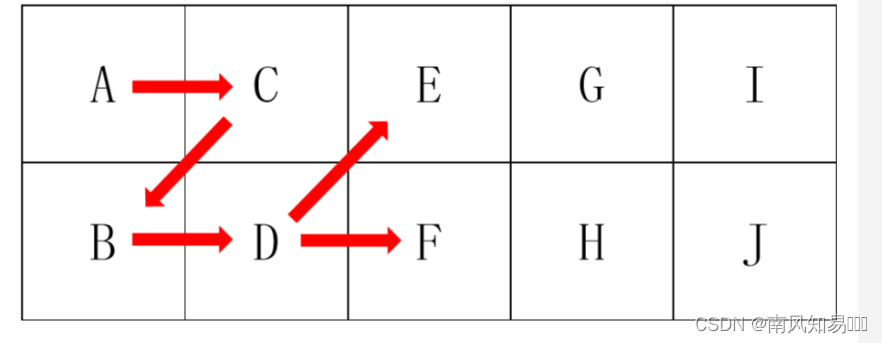
在这里插入图片描述

假设从顶点A出发，那么其有两条路线：A->C->B->D或A->D->B->C，假设到了点D，则D又可以有两种选择（要么到E要么到F），此时又可再重复在点A的行为，直到最终到达矩形的另一侧
显然这也属于“一趟过去，不再返回”的类型，因此也用数组a来表示，则可以把问题规模转换成a[ i-2 ]
于是得到状态转移方程：a[ i ] = 2 × 2 × a[ i-2 ] （第一个乘2是选C或D，二个乘2是选E或F）

2.从中间出发

在这里插入图片描述
我们从图中i=3(E点)处出发（以i为分割线，将图分为左边的ABCDEF以及右边的GHIJ），为了遍历所有格子，我们需要先走完左边的这个整体（特别注意：这里必须倒回到F才能继续走右边），然后再把右边视为以G或者H为起点的一组格子将其走完（因此这里需要乘以2，两种起点出发嘛）
分析上述的流程，可以得到从中间出发的方案数为：( b[ i ] ) × ( 2 × a[ n-i ] )
同理，我们可以先走右边的EFGHIJ，然后再走左边的ABCD
这样的方案数为：(b[ n-i+1]) × (2×a[ i - 1])
由于上面的所有起始点都是以E为出发点行走的，我们同理也可以以F为起点出发，那么从第i列开始刷漆的方法就有:[ (b[ i ])×(2×a[ n-i ])+(b[ n-i+1])×(2×a[ i - 1]) ]×2

用动态规划法，

package com.lanqiao2013;import java.util.Scanner;public class GeZiShuayouqiDemo {static final long MOD=1000000007;public static void main(String[] args) {Scanner scanner = new Scanner(System.in);int n = 0;n= scanner.nextInt();scanner.close();if(n==1) { System.out.println(2);return;}	long[] a = new long[1005];long[] b = new long[1005];// base casea[1] = 1;a[2] = 6;b[1] = 1;b[2] = 2;// 从四个角开始for (int i = 3; i <= n; i++) {b[i] = (2 * b[i - 1])%MOD;a[i] = (2 * a[i - 1] + b[i] + 2 * 2 * a[i - 2])%MOD;}long sum = 4 * a[n]%MOD;// 从中间开始for (int i = 2; i < n; i++) {sum = (sum + ((b[i]) * (2 *a[n - i]) + (b[n - i + 1]) * (2 * a[i - 1])) * 2)%MOD;}System.out.println(sum);}}