Codeforces 1186 F. Vus the Cossack and a Graph —— 线段树，贪心

本文主要是介绍Codeforces 1186 F. Vus the Cossack and a Graph —— 线段树，贪心，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

This way

题意：

现在有一张简单图，n个点m条边，让你留下最多$\lceil \frac{n+m}{2}\rceil$条边，假设每个点的当前度数为di，每个点的最终度数要大于等于$\lceil \frac{d_i}{2}\rceil$。问你留下来哪些边

题解：

我最近做题目都先考虑线段树是否能做…不知道这是不是一个好习惯，但是这道题依旧还是用线段树过了。
首先我考虑减少当前度数最大的点的边，然后和这个点相连的那些点应该删谁？如果删除度数较大的那个的话：

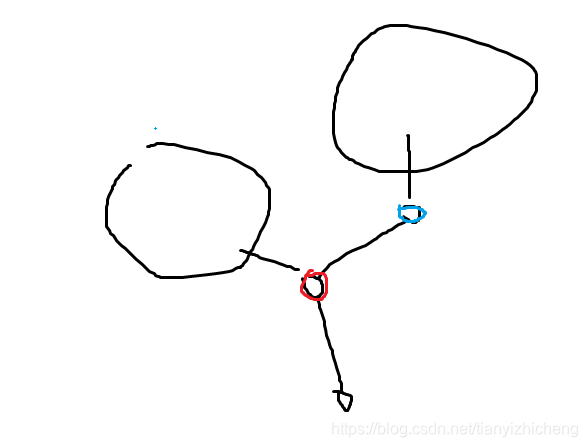
就比如当前是红色的点的度数最大，蓝色的点的度数比黑色的点的度数大，如果我删掉蓝色的点和红色点的连边，就有可能红色的点的度数正好变成了最小值，那么红黑两点的边就不能删了，这样可能会导致错误。如果删掉红黑两点的边，那么蓝色就可以和它连的别的点继续删。所以我每次找出最大的度数的点之后，对于它连的点按照度数为关键字从小到大排序，然后在合法的情况下依次删掉。
每个点做完之后，这个点下次就不能在被找到，那么就要在线段树中将其抹去。

#include<bits/stdc++.h>
using namespace std;
#define pa pair<int,int>
const int N=1e6+5;
int d[N],f[N];
vector<int>vec[N];
pa mx[N*4];
void build(int l,int r,int root){if(l==r){mx[root]={l,f[l]};return ;}int mid=l+r>>1;build(l,mid,root<<1);build(mid+1,r,root<<1|1);if(mx[root<<1].second>=mx[root<<1|1].second)mx[root]=mx[root<<1];elsemx[root]=mx[root<<1|1];
}
void update(int l,int r,int root,int p,int v){if(l==r){mx[root].second+=v;return ;}int mid=l+r>>1;if(mid>=p)update(l,mid,root<<1,p,v);elseupdate(mid+1,r,root<<1|1,p,v);if(mx[root<<1].second>=mx[root<<1|1].second)mx[root]=mx[root<<1];elsemx[root]=mx[root<<1|1];
}
struct edge{int x,y;
}e[N];
unordered_map<int,bool>del[N];
vector<pa>s;
int main()
{int n,m;scanf("%d%d",&n,&m);for(int i=1;i<=m;i++){scanf("%d%d",&e[i].x,&e[i].y);vec[e[i].x].push_back(e[i].y),vec[e[i].y].push_back(e[i].x);f[e[i].y]++,f[e[i].x]++;}for(int i=1;i<=n;i++)d[i]=(f[i]+1)/2;int res=(m-n)/2;build(1,n,1);while(res>0){s.clear();int x=mx[1].first;for(auto i:vec[x]){if(del[x].count(i)||f[i]==d[i])continue;s.push_back({f[i],i});}sort(s.begin(),s.end());for(auto i:s){f[i.second]--,f[x]--,res--;update(1,n,1,i.second,-1);del[i.second][x]=del[x][i.second]=1;if(f[x]==d[x])break;}update(1,n,1,x,-1e9);}printf("%d\n",m-(m-n)/2+res);for(int i=1;i<=m;i++){if(del[e[i].x].count(e[i].y))continue;printf("%d %d\n",e[i].x,e[i].y);}return 0;
}

这篇关于Codeforces 1186 F. Vus the Cossack and a Graph —— 线段树，贪心的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---