视觉SLAM学习打卡【8-2】-视觉里程计·直接法代码详解

2024-04-06 09:28
文章标签 代码 学习 详解 打卡 slam 视觉 直接 里程计

本文主要是介绍视觉SLAM学习打卡【8-2】-视觉里程计·直接法代码详解，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

视觉SLAM学习打卡【8-2】-视觉里程计·直接法代码详解

  • 1. 光流法 optical_flow.cpp
    • （1）理论推导：双线性插值
    • （2）GFTTDetector函数介绍
    • （3）梯度计算
  • 2. 直接法 direct_method.cpp
  • 3. 报错解决方案
    • （1）路径问题
    • （2）opencv4安装

1. 光流法 optical_flow.cpp

// 引入OpenCV库，它包含了计算机视觉任务所需的各种函数和数据结构  
#include <opencv2/opencv.hpp>  // 引入C++标准库中的string，用于处理字符串，如文件路径  
#include <string>  // 引入C++标准库中的chrono，通常用于计时和性能评估  
#include <chrono>  // 引入Eigen库的核心和密集矩阵模块，Eigen是一个高级C++库，用于进行线性代数、矩阵和向量操作  
#include <Eigen/Core>  
#include <Eigen/Dense>  // 使用C++标准库的命名空间，以便更方便地访问其函数和对象  
using namespace std;  // 使用OpenCV的命名空间，以便更方便地访问其函数和对象  
using namespace cv;  // 定义两个字符串变量，分别存储两个图像文件的路径  
string file_1 = "./LK1.png";  // 第一个图像文件路径  
string file_2 = "./LK2.png";  // 第二个图像文件路径  // 定义一个名为OpticalFlowTracker的类，用于光流跟踪和相关接口  
class OpticalFlowTracker {  
public:  // 构造函数，初始化类的成员变量，并接收一系列参数，包括两张图像、关键点集合、成功跟踪的标志等  OpticalFlowTracker(  const Mat &img1_,  // 第一张图像  const Mat &img2_,  // 第二张图像  const vector<KeyPoint> &kp1_,  // 在第一张图像中检测到的关键点  vector<KeyPoint> &kp2_,  // 在第二张图像中对应的关键点（输出参数）  vector<bool> &success_,  // 跟踪成功的标志（输出参数）  bool inverse_ = true,  // 是否使用逆向光流法，默认为true  bool has_initial_ = false  // 是否已有初始猜测，默认为false  ) :  img1(img1_), img2(img2_), kp1(kp1_), kp2(kp2_), success(success_), inverse(inverse_),  has_initial(has_initial_) {}  // 初始化列表，为成员变量赋值  // 成员函数，计算给定范围内的光流  void calculateOpticalFlow(const Range &range);    private:  // 类的私有成员变量，包括两张图像、关键点集合、跟踪成功的标志等  const Mat &img1;  // 第一张图像  const Mat &img2;  // 第二张图像  const vector<KeyPoint> &kp1;  // 在第一张图像中检测到的关键点  vector<KeyPoint> &kp2;  // 在第二张图像中对应的关键点  vector<bool> &success;  // 跟踪成功的标志  bool inverse = true;  // 是否使用逆向光流法  bool has_initial = false;  // 是否已有初始猜测  
};  /**  * 单层光流法函数声明，用于计算两张图像之间的光流  * @param [in] img1 第一张图像  * @param [in] img2 第二张图像  * @param [in] kp1 在第一张图像中检测到的关键点  * @param [in|out] kp2 在第二张图像中对应的关键点，如果为空，则使用kp1中的初始猜测  * @param [out] success 跟踪成功的标志  * @param [in] inverse 是否使用逆向光流法，默认为false  * @param [in] has_initial_guess 是否已有初始猜测，默认为false  */  
void OpticalFlowSingleLevel(  const Mat &img1,  // 第一张图像  const Mat &img2,  // 第二张图像  const vector<KeyPoint> &kp1,  // 在第一张图像中检测到的关键点  vector<KeyPoint> &kp2,  // 在第二张图像中对应的关键点（可能是输出参数）  vector<bool> &success,  // 跟踪成功的标志（输出参数）  bool inverse = false,  // 是否使用逆向光流法，默认为false  bool has_initial_guess = false  // 是否已有初始猜测，默认为false  
);  /**  * 多层光流法函数声明，用于计算两张图像之间的光流，使用图像金字塔来提高精度和稳定性   * @param [in] img1 第一张图像金字塔  * @param [in] img2 第二张图像金字塔  * @param [in] kp1 在第一张图像中检测到的关键点  * @param [out] kp2 在第二张图像中对应的关键点  * @param [out] success 跟踪成功的标志  * @param [in] inverse 是否启用逆向光流法来提高精度和稳定性，特别是在快速运动时  */  
// 函数声明：多层光流法，用于在两张图像之间计算关键点的光流  
void OpticalFlowMultiLevel(  const Mat &img1,  // 第一张图像  const Mat &img2,  // 第二张图像  const vector<KeyPoint> &kp1,  // 第一张图像中的关键点  vector<KeyPoint> &kp2,  // 第二张图像中对应的关键点（输出参数）  vector<bool> &success,  // 跟踪成功的标志（输出参数）  bool inverse = false  // 是否使用逆向光流法，默认为false  
);  /**  * 从参考图像中获取灰度值（双线性插值）  * @param img 输入图像  * @param x 浮点型x坐标  * @param y 浮点型y坐标  * @return 插值后的像素值  */  // 定义一个内联函数，用于通过双线性插值从图像中获取灰度值  
inline float GetPixelValue(const cv::Mat &img, float x, float y) {  // 边界检查，确保坐标在图像范围内  if (x < 0) x = 0;  if (y < 0) y = 0;  if (x >= img.cols - 1) x = img.cols - 2;  if (y >= img.rows - 1) y = img.rows - 2;  // 计算插值所需的权重  float xx = x - floor(x);  float yy = y - floor(y);  int x_a1 = std::min(img.cols - 1, int(x) + 1);  // 确保x坐标不超出图像边界  int y_a1 = std::min(img.rows - 1, int(y) + 1);  // 确保y坐标不超出图像边界  // 进行双线性插值计算  return (1 - xx) * (1 - yy) * img.at<uchar>(y, x) +  // 左下角像素的权重和值  xx * (1 - yy) * img.at<uchar>(y, x_a1) +  // 右下角像素的权重和值  (1 - xx) * yy * img.at<uchar>(y_a1, x) +  // 左上角像素的权重和值  xx * yy * img.at<uchar>(y_a1, x_a1);  // 右上角像素的权重和值  
}  // 主函数  
int main(int argc, char **argv) {  // 读取两张图像，注意它们是灰度图像（CV_8UC1），不是彩色图像（CV_8UC3）  Mat img1 = imread(file_1, 0);  // 读取第一张图像为灰度图  Mat img2 = imread(file_2, 0);  // 读取第二张图像为灰度图  // 检测关键点，这里使用GFTT（Good Features To Track）方法  vector<KeyPoint> kp1;  // 存储第一张图像中的关键点  Ptr<GFTTDetector> detector = GFTTDetector::create(500, 0.01, 20);  // 最多检测500个关键点，其他参数为算法设置  detector->detect(img1, kp1);  // 在第一张图像中检测关键点  // 接下来在第二张图像中跟踪这些关键点  // 首先使用单层LK光流法进行测试  vector<KeyPoint> kp2_single;  // 存储单层LK光流法跟踪到的关键点  vector<bool> success_single;  // 存储单层LK光流法跟踪成功的标志  OpticalFlowSingleLevel(img1, img2, kp1, kp2_single, success_single);  // 执行单层LK光流法  // 然后测试多层LK光流法  vector<KeyPoint> kp2_multi;  // 存储多层LK光流法跟踪到的关键点  vector<bool> success_multi;  // 存储多层LK光流法跟踪成功的标志  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();  // 记录开始时间  OpticalFlowMultiLevel(img1, img2, kp1, kp2_multi, success_multi, true);  // 执行多层LK光流法，启用逆向光流  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();  // 记录结束时间  auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);  // 计算执行时间  cout << "optical flow by gauss-newton: " << time_used.count() << endl;  // 输出执行时间  // 使用OpenCV的calcOpticalFlowPyrLK函数进行验证  vector<Point2f> pt1, pt2;  // 存储输入和输出的关键点位置  for (auto &kp: kp1) pt1.push_back(kp.pt);  // 将关键点位置转换为OpenCV的点格式  vector<uchar> status;  // 存储每个关键点的跟踪状态  vector<float> error;  // 存储每个关键点的跟踪误差  t1 = chrono::steady_clock::now();  // 记录开始时间  cv::calcOpticalFlowPyrLK(img1, img2, pt1, pt2, status, error);  // 执行OpenCV的光流法函数  t2 = chrono::steady_clock::now();  // 记录结束时间  time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);  // 计算执行时间  cout << "optical flow by opencv: " << time_used.count() << endl;  // 输出执行时间  
}
// 转换img2图像从灰度到BGR颜色空间，以便在彩色图像上绘制  
Mat img2_single;  
cv::cvtColor(img2, img2_single, CV_GRAY2BGR);  // 遍历关键点kp2_single，这些关键点可能是在单尺度上检测到的特征点  
for (int i = 0; i < kp2_single.size(); i++) {  // 如果当前关键点匹配成功（由success_single数组标记）  if (success_single[i]) {  // 在匹配的关键点位置上画一个绿色的圆圈，表示匹配成功的位置  cv::circle(img2_single, kp2_single[i].pt, 2, cv::Scalar(0, 250, 0), 2);  // 画一条从kp1[i]到kp2_single[i]的线，表示两个图像之间的关键点匹配  cv::line(img2_single, kp1[i].pt, kp2_single[i].pt, cv::Scalar(0, 250, 0));  }  
}  // 与上面的操作类似，但是这次是针对多尺度检测到的关键点  
Mat img2_multi;  
cv::cvtColor(img2, img2_multi, CV_GRAY2BGR);  
for (int i = 0; i < kp2_multi.size(); i++) {  if (success_multi[i]) {  cv::circle(img2_multi, kp2_multi[i].pt, 2, cv::Scalar(0, 250, 0), 2);  cv::line(img2_multi, kp1[i].pt, kp2_multi[i].pt, cv::Scalar(0, 250, 0));  }  
}  // 这里的操作与上面类似，但是使用的是OpenCV函数找到的匹配点  
Mat img2_CV;  
cv::cvtColor(img2, img2_CV, CV_GRAY2BGR);  
for (int i = 0; i < pt2.size(); i++) {  if (status[i]) { // status数组表示每个点的匹配状态  cv::circle(img2_CV, pt2[i], 2, cv::Scalar(0, 250, 0), 2);  cv::line(img2_CV, pt1[i], pt2[i], cv::Scalar(0, 250, 0));  }  
}  // 显示三个处理后的图像窗口  
cv::imshow("tracked single level", img2_single); // 显示单尺度跟踪结果  
cv::imshow("tracked multi level", img2_multi);  // 显示多尺度跟踪结果  
cv::imshow("tracked by opencv", img2_CV);       // 显示OpenCV跟踪结果  // 等待用户按键，然后继续执行后续代码（如果有的话）或退出程序  
cv::waitKey(0);  return 0; // 程序正常退出，返回0
// OpticalFlowSingleLevel函数用于计算两个图像之间的光流  
void OpticalFlowSingleLevel(  const Mat &img1, // 第一个图像  const Mat &img2, // 第二个图像  const vector<KeyPoint> &kp1, // 第一个图像中的关键点  vector<KeyPoint> &kp2, // 第二个图像中匹配的关键点，将会被计算和填充  vector<bool> &success, // 标记每个关键点是否成功匹配  bool inverse, // 是否使用逆向光流法  bool has_initial) { // 是否有初始估计值  kp2.resize(kp1.size()); // 调整kp2的大小以匹配kp1的大小  success.resize(kp1.size()); // 调整success的大小以匹配kp1的大小  // 创建一个OpticalFlowTracker对象来处理光流计算  OpticalFlowTracker tracker(img1, img2, kp1, kp2, success, inverse, has_initial);  // 使用并行计算来加速光流计算过程  parallel_for_(Range(0, kp1.size()),  std::bind(&OpticalFlowTracker::calculateOpticalFlow, &tracker, placeholders::_1));  
}  // OpticalFlowTracker类的成员函数，用于计算指定范围内的光流  
void OpticalFlowTracker::calculateOpticalFlow(const Range &range) {  int half_patch_size = 4; // 补丁的一半大小，用于定义关键点周围的区域  int iterations = 10; // Gauss-Newton迭代的次数  // 遍历指定范围内的所有关键点  for (size_t i = range.start; i < range.end; i++) {  auto kp = kp1[i]; // 获取当前关键点  double dx = 0, dy = 0; // 初始化光流的x和y分量  // 如果有初始估计，则从kp2中获取dx和dy的初始值  if (has_initial) {  dx = kp2[i].pt.x - kp.pt.x;  dy = kp2[i].pt.y - kp.pt.y;  }  double cost = 0, lastCost = 0; // 初始化代价和上一次迭代的代价  bool succ = true; // 标记当前关键点是否成功匹配  // 使用Gauss-Newton方法进行迭代优化  Eigen::Matrix2d H = Eigen::Matrix2d::Zero(); // 初始化Hessian矩阵  Eigen::Vector2d b = Eigen::Vector2d::Zero(); // 初始化bias向量  Eigen::Vector2d J; // 初始化Jacobian向量  // 进行迭代优化  for (int iter = 0; iter < iterations; iter++) {  // 根据是否是逆向模式来重置H和b  if (!inverse) {  H = Eigen::Matrix2d::Zero();  b = Eigen::Vector2d::Zero();  } else {  b = Eigen::Vector2d::Zero();  }  cost = 0; // 重置代价  // 在关键点周围的区域内计算代价和Jacobian  for (int x = -half_patch_size; x < half_patch_size; x++) {  for (int y = -half_patch_size; y < half_patch_size; y++) {  // 计算两个图像在对应位置的像素值差（即误差）  double error = GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y) -  GetPixelValue(img2, kp.pt.x + x + dx, kp.pt.y + y + dy);  // 根据是否是逆向模式来计算Jacobian  if (!inverse) {  // ...（省略了梯度J的计算过程）  } else if (iter == 0) {  // ...（省略了梯度J的计算过程）  }  // 更新b, H和代价  b += -error * J;  cost += error * error;  if (!inverse || iter == 0) {  H += J * J.transpose();  }  }  }  // 使用LDLT分解来求解更新量  Eigen::Vector2d update = H.ldlt().solve(b);  // 检查更新量是否有效  if (std::isnan(update[0])) {  // 如果更新量是NaN，则表示失败  cout << "update is nan" << endl;  succ = false;  break;  }  // 检查代价是否降低，如果没有则退出循环  if (iter > 0 && cost > lastCost) {  break;  }  // 更新dx, dy和上一次迭代的代价  dx += update[0];  dy += update[1];  lastCost = cost;  succ = true;  // 检查是否收敛，如果更新量很小则退出循环  if (update.norm() < 1e-2) {  break;  }  }  // 设置成功匹配的标记和第二个图像中的关键点位置  success[i] = succ;  kp2[i].pt = kp.pt + Point2f(dx, dy);  }  
}
// 定义一个多层光流法跟踪函数  
void OpticalFlowMultiLevel(  const Mat &img1, // 第一个图像  const Mat &img2, // 第二个图像  const vector<KeyPoint> &kp1, // 第一个图像中的关键点  vector<KeyPoint> &kp2, // 第二个图像中对应的关键点，为输出参数  vector<bool> &success, // 跟踪是否成功的标志位，为输出参数  bool inverse // 是否反向跟踪（从第二帧跟踪到第一帧）  
) {  // 设定金字塔的层数和每层之间的缩放比例  int pyramids = 4;  double pyramid_scale = 0.5;  double scales[] = {1.0, 0.5, 0.25, 0.125}; // 各层金字塔的缩放比例  // 开始计时，用于计算构建金字塔所用的时间  chrono::steady_clock::time_point t1 = chrono::steady_clock::now();  vector<Mat> pyr1, pyr2; // 定义两个图像金字塔  // 构建图像金字塔  for (int i = 0; i < pyramids; i++) {  if (i == 0) {  pyr1.push_back(img1); // 第一层为原图  pyr2.push_back(img2);  } else {  Mat img1_pyr, img2_pyr;  // 对上一层的图像进行缩放，得到当前层的图像  cv::resize(pyr1[i - 1], img1_pyr,  cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));  cv::resize(pyr2[i - 1], img2_pyr,  cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));  pyr1.push_back(img1_pyr); // 将当前层的图像添加到金字塔中  pyr2.push_back(img2_pyr);  }  }  // 结束计时，并输出构建金字塔所用的时间  chrono::steady_clock::time_point t2 = chrono::steady_clock::now();  auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);  cout << "build pyramid time: " << time_used.count() << endl;  // 将原图中的关键点按照最底层的缩放比例进行缩放，以便在金字塔的最顶层进行跟踪  vector<KeyPoint> kp1_pyr, kp2_pyr;  for (auto &kp:kp1) {  auto kp_top = kp;  kp_top.pt *= scales[pyramids - 1]; // 按照最底层的缩放比例进行缩放  kp1_pyr.push_back(kp_top); // 添加到关键点金字塔中  kp2_pyr.push_back(kp_top);  }  // 从金字塔的顶层开始，向下逐层进行跟踪  for (int level = pyramids - 1; level >= 0; level--) {  success.clear(); // 清空上一层的跟踪成功标志位  t1 = chrono::steady_clock::now(); // 开始计时  // 在当前层进行光流法跟踪  OpticalFlowSingleLevel(pyr1[level], pyr2[level], kp1_pyr, kp2_pyr, success, inverse, true);  t2 = chrono::steady_clock::now(); // 结束计时  // 输出当前层的跟踪时间  auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);  cout << "track pyr " << level << " cost time: " << time_used.count() << endl;  // 如果不是最底层，则将关键点的位置按照缩放比例进行放大，以便在下一层进行跟踪  if (level > 0) {  for (auto &kp: kp1_pyr)  kp.pt /= pyramid_scale;  for (auto &kp: kp2_pyr)  kp.pt /= pyramid_scale;  }  }  // 将最终跟踪到的关键点添加到输出参数中  for (auto &kp: kp2_pyr)  kp2.push_back(kp);  
}

注：上述路径需改为绝对路径.

（1）理论推导：双线性插值

首先，来看单线性插值（双线性插值可看作3次双线性插值）
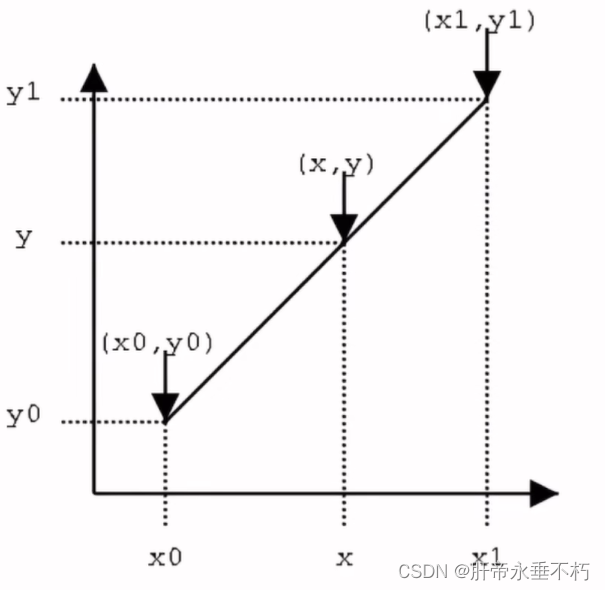
在这里插入图片描述
由斜率相等可得 y − y 0 x − x 0 = y 1 − y 0 x 1 − x 0 \frac{y-y_{0}}{x-x_{0}}=\frac{y_{1}-y_{0}}{x_{1}-x_{0}} x−x0​y−y0​​=x1​−x0​y1​−y0​​化简得 y = x 1 − x x 1 − x 0 y 0 + x − x 0 x 1 − x 0 y 1 y=\frac{x_{1}-x}{x_{1}-x_{0}}y_{0}+\frac{x_{-}x_{0}}{x_{1}-x_{0}}y_{1} y=x1​−x0​x1​−x​y0​+x1​−x0​x−​x0​​y1​把y看作函数值P P = x 1 − x x 1 − x 0 P 0 + x − x 0 x 1 − x 0 P 1 . P=\frac{x_{1}-x}{x_{1}-x_{0}}P_{0}+\frac{x-x_{0}}{x_{1}-x_{0}}P_{1}. P=x1​−x0​x1​−x​P0​+x1​−x0​x−x0​​P1​.
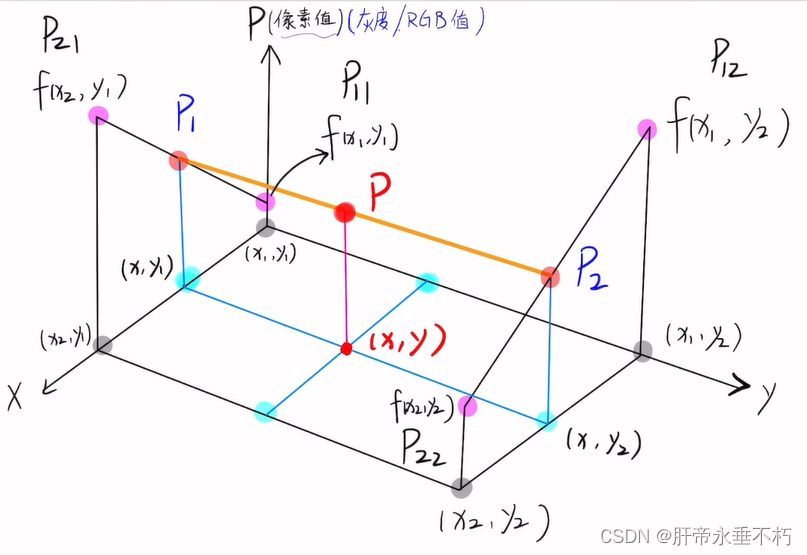
在这里插入图片描述
以左梯形面作x方向上的线性插值，即在这里插入图片描述
P 1 = x 2 − x x 2 − x 1 P 11 + x − x 1 x 2 − x 1 P 21 P_{1}=\frac{x_{2}-x}{x_{2}-x_{1}} P_{11} +\frac{x-x_{1}}{x_{2}-x_{1}} P_{21} P1​=x2​−x1​x2​−x​P11​+x2​−x1​x−x1​​P21​
以右梯形面作x方向上的线性插值，即
在这里插入图片描述
P 2 = x 2 − x x 2 − x 1 P 12 + x − x 1 x 2 − x 1 P 22 P_{2}=\frac{x_{2}-x}{x_{2}-x_{1}}P_{12}+\frac{x-x_{1}}{x_{2}-x_{1}}P_{22} P2​=x2​−x1​x2​−x​P12​+x2​−x1​x−x1​​P22​以中间梯形面作y方向上的线性插值，即在这里插入图片描述
P = y 2 − y y 2 − y 1 P 1 + y − y 1 y 2 − y 1 p 2 P=\frac{y_{2}-y}{y_{2}-y_{1}} P_{1}+\frac{y-y_{1}}{y_{2}-y_{1}} p_{2} P=y2​−y1​y2​−y​P1​+y2​−y1​y−y1​​p2​将P1、P2代入上式得 P = P 11 ( x 2 − x 1 ) ( y 2 − y 1 ) ( x 2 − x 1 ) ( y 2 − y ) + P 21 ( x 2 − x 1 ) ( y 2 − y 1 ) ( x − x 1 ) ( y 2 − y ) + P 12 ( x 2 − x 1 ) ( y 2 − y 1 ) ( x 2 − x 1 ) ( y − y 1 ) + P 22 ( x 2 − x 1 ) ( y 2 − y 1 ) ( x − x 1 ) ( y − y 1 ) \begin{gathered} P=\frac{P_{11}}{(x_{2}-x_{1})(y_{2}-y_{1})}(x_{2}-x_{1})(y_{2}-y)+\frac{P_{21}}{(x_{2}-x_{1})(y_{2}-y_{1})}(x-x_{1})(y_{2}-y)+ \\ \frac{P_{12}}{(x_{2}-x_{1})(y_{2}-y_{1})}(x_{2}-x_{1})(y-y_{1})+\frac{P_{22}}{(x_{2}-x_{1})(y_{2}-y_{1})}(x-x_{1})(y-y_{1}) \\\end{gathered} P=(x2​−x1​)(y2​−y1​)P11​​(x2​−x1​)(y2​−y)+(x2​−x1​)(y2​−y1​)P21​​(x−x1​)(y2​−y)+(x2​−x1​)(y2​−y1​)P12​​(x2​−x1​)(y−y1​)+(x2​−x1​)(y2​−y1​)P22​​(x−x1​)(y−y1​)​由于相邻四个点x,y只差1，即在这里插入图片描述
所以，上式化简为 P = P 11 ( x 2 − x ) ( y 2 − y ) + P 21 ( x − x 1 ) ( y 2 − y ) + P 12 ( x 2 − x ) ( y − y 1 ) + P 22 ( x − x 1 ) ( y − y 1 ) \begin{aligned}P&=P_{11}(x_2-x)(y_2-y)+P_{21}(x-x_1)(y_2-y)\\&+P_{12}(x_2-x)(y-y_1)+P_{22}(x-x_1)(y-y_1)\end{aligned} P​=P11​(x2​−x)(y2​−y)+P21​(x−x1​)(y2​−y)+P12​(x2​−x)(y−y1​)+P22​(x−x1​)(y−y1​)​【直通车】——附：参考自视频-图像处理·双线性插值

（2）GFTTDetector函数介绍

Ptr<GFTTDetector> detector = GFTTDetector::create(500, 0.01, 20);

这行代码是在使用OpenCV库创建一个GFTT（Good Features to Track）检测器对象。GFTT是一个计算机视觉中用于特征点检测的方法，常用于目标跟踪、图像拼接等应用中。

Ptr detector：这里定义了一个指向GFTTDetector类的智能指针detector。Ptr是OpenCV中的一个模板类，用于自动管理对象的生命周期，类似于C++11中的std::shared_ptr。当Ptr对象超出其作用域或被重置时，它会自动删除其所指向的对象。

GFTTDetector::create(500, 0.01, 20)：这是调用GFTTDetector类的静态成员函数create来创建一个GFTTDetector实例。这个函数接受三个参数：

  • 500：这是要检测的最大特征点数量。在这个例子中，检测器将尝试找到最多500个特征点。
  • 0.01：这是特征点检测的质量等级，值范围通常在0到1之间（或表示为百分比）。这个值越高，检测到的特征点就越少，但每个特征点的“质量”或“独特性”通常也越高。这里的0.01是一个相对较低的值，意味着检测器会尝试找到相对较多的特征点，尽管它们可能不是最独特或最显著的。
  • 20：这是两个特征点之间的最小距离。这有助于确保检测到的特征点在图像中分布均匀，而不是都集中在图像的某个特定区域。

总的来说，这行代码创建了一个GFTTDetector对象，该对象被配置为在图像中查找最多500个特征点，这些特征点的质量至少为0.01，并且特征点之间的最小距离为20个像素单位。这个检测器之后可以用于在图像中查找符合这些条件的特征点。

（3）梯度计算

J = -1.0 * Eigen::Vector2d(0.5 * (GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) -GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y)),0.5 * (GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) -GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1))

这段代码是在计算图像中某个关键点（kp）附近像素的强度梯度。具体地说，它是在一个二维图像（img1）中，对于给定的关键点位置（kp.pt.x, kp.pt.y），计算该点在水平和垂直方向上的强度梯度。这里的x和y可能是相对于关键点位置的某个偏移量，用于在关键点周围的某个具体位置计算梯度。

水平梯度计算：

  • GetPixelValue(img1, kp.pt.x + x + 1, kp.pt.y + y) 获取关键点右侧紧邻像素的值。
  • GetPixelValue(img1, kp.pt.x + x - 1, kp.pt.y + y) 获取关键点左侧紧邻像素的值。
  • 两者之差的一半表示该点在水平方向上的梯度（或称为x方向上的导数近似值）。

垂直梯度计算：

  • GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y + 1) 获取关键点下侧紧邻像素的值。
  • GetPixelValue(img1, kp.pt.x + x, kp.pt.y + y - 1) 获取关键点上侧紧邻像素的值。
  • 两者之差的一半表示该点在垂直方向上的梯度（或称为y方向上的导数近似值）。

最后，这两个梯度值被组合成一个Eigen::Vector2d类型的向量J，其中J[0]是水平梯度，J[1]是垂直梯度。

这种梯度计算在计算机视觉中非常常见，特别是在特征检测、光流估计、图像配准等任务中。梯度提供了关于图像局部强度和方向变化的重要信息。在这个例子中，负号可能是为了将梯度方向与强度增加的方向对应起来（这取决于具体的梯度定义和后续应用）。不过，在很多情况下，梯度的具体方向并不是关键，而是其大小和方向的变化更为重要。

2. 直接法 direct_method.cpp

// 引入OpenCV库，一个开源的计算机视觉和机器学习库  
#include <opencv2/opencv.hpp>  
// 引入Sophus库，一个用于处理3D变换（如旋转和平移）的C++库  
#include <sophus/se3.hpp>  
// 引入Boost库中的format模块，用于字符串格式化  
#include <boost/format.hpp>  
//一个用于视觉SLAM的轻量级GUI库
#include <pangolin/pangolin.h>  // 注意：这里可能是拼写错误，应该是Pangolin而不是Pangolin  // 使用C++标准库的命名空间  
using namespace std;  // 定义一个使用Eigen对齐分配器的vector，用于存储2D向量  
typedef vector<Eigen::Vector2d, Eigen::aligned_allocator<Eigen::Vector2d>> VecVector2d;  // 相机内参 
double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;  
// 双目相机的基线长度  
double baseline = 0.573;  
// 图像文件的路径  
string left_file = "./left.png";  
string disparity_file = "./disparity.png";  
// 用于格式化文件名的boost::format对象  
boost::format fmt_others("./%06d.png"); // 其他文件  // 定义一些方便的别名  
typedef Eigen::Matrix<double, 6, 6> Matrix6d;  // 6x6的双精度矩阵  
typedef Eigen::Matrix<double, 2, 6> Matrix26d; // 2x6的双精度矩阵  
typedef Eigen::Matrix<double, 6, 1> Vector6d;  // 6x1的双精度向量  /// 用于并行计算中累积雅可比矩阵的类  
class JacobianAccumulator {  
public:  // 构造函数，初始化类的成员变量  JacobianAccumulator(  const cv::Mat &img1_,  // 第一张图像  const cv::Mat &img2_,  // 第二张图像  const VecVector2d &px_ref_,  // 参考像素坐标  const vector<double> depth_ref_,  // 参考像素对应的深度值  Sophus::SE3d &T21_)  // 从第一个相机到第二个相机的变换矩阵  : img1(img1_), img2(img2_), px_ref(px_ref_), depth_ref(depth_ref_), T21(T21_) {  // 初始化投影点的vector，大小和px_ref相同，初始值为(0, 0)  projection = VecVector2d(px_ref.size(), Eigen::Vector2d(0, 0));  }  // 在给定的范围内累积雅可比矩阵  void accumulate_jacobian(const cv::Range &range);  // 获取海森矩阵  Matrix6d hessian() const { return H; }  // 获取偏差向量  Vector6d bias() const { return b; }  // 获取总代价  double cost_func() const { return cost; }  // 获取投影点  VecVector2d projected_points() const { return projection; }  // 重置H, b, cost为0  void reset() {  H = Matrix6d::Zero();  // 将H初始化为6x6的零矩阵  b = Vector6d::Zero();  // 将b初始化为6x1的零向量  cost = 0;  // 将代价重置为0  }  private:  // 成员变量：两张图像、参考像素坐标、参考深度值、相机间的变换矩阵、投影点等  const cv::Mat &img1;  const cv::Mat &img2;  const VecVector2d &px_ref;  const vector<double> depth_ref;  Sophus::SE3d &T21;  VecVector2d projection;  // 投影点  // 用于保护海森矩阵H的互斥锁（在多线程环境中防止数据竞争）  std::mutex hessian_mutex;    Matrix6d H = Matrix6d::Zero();  // 初始化为6x6的零矩阵，用于存储海森矩阵  Vector6d b = Vector6d::Zero();  // 初始化为6x1的零向量，用于存储偏差向量  double cost = 0;  // 代价函数的值，初始化为0  
};
/**  * 使用直接法进行位姿估计  * @param img1 第一个图像  * @param img2 第二个图像  * @param px_ref 参考像素坐标  * @param depth_ref 参考像素的深度值  * @param T21 从第一个相机到第二个相机的变换矩阵  */  
void DirectPoseEstimationMultiLayer(  const cv::Mat &img1,  const cv::Mat &img2,  const VecVector2d &px_ref,  const vector<double> depth_ref,  Sophus::SE3d &T21  
); // 此函数定义了一个多层直接法位姿估计的接口/**  * 使用直接法进行位姿估计（单层）  * @param img1 第一个图像  * @param img2 第二个图像  * @param px_ref 参考像素坐标  * @param depth_ref 参考像素的深度值  * @param T21 从第一个相机到第二个相机的变换矩阵  */  
void DirectPoseEstimationSingleLayer(  const cv::Mat &img1,  const cv::Mat &img2,  const VecVector2d &px_ref,  const vector<double> depth_ref,  Sophus::SE3d &T21  
); // 此函数定义了一个单层直接法位姿估计的接口// 双线性插值函数  
inline float GetPixelValue(const cv::Mat &img, float x, float y) {  // 边界检查  if (x < 0) x = 0;  if (y < 0) y = 0;  if (x >= img.cols) x = img.cols - 1;  if (y >= img.rows) y = img.rows - 1;  // 获取像素位置对应的指针  uchar *data = &img.data[int(y) * img.step + int(x)];  float xx = x - floor(x);  float yy = y - floor(y);  // 进行双线性插值计算像素值  return float(  (1 - xx) * (1 - yy) * data[0] +  xx * (1 - yy) * data[1] +  (1 - xx) * yy * data[img.step] +  xx * yy * data[img.step + 1]  );  
}  int main(int argc, char **argv) {  // 读取左图像和视差图像  cv::Mat left_img = cv::imread(left_file, 0);  cv::Mat disparity_img = cv::imread(disparity_file, 0);  // 使用随机数生成器在左图像中随机选择像素，并生成对应的三维点  cv::RNG rng;  int nPoints = 2000; // 选择的点数  int boarder = 20; // 边界宽度，避免选择图像边缘的像素  VecVector2d pixels_ref; // 参考像素坐标  vector<double> depth_ref; // 参考像素的深度值  // 在左图像中随机选择像素，并计算其深度值  for (int i = 0; i < nPoints; i++) {  int x = rng.uniform(boarder, left_img.cols - boarder);  int y = rng.uniform(boarder, left_img.rows - boarder);  int disparity = disparity_img.at<uchar>(y, x); // 获取视差值  double depth = fx * baseline / disparity; // 计算深度值  depth_ref.push_back(depth); // 存储深度值  pixels_ref.push_back(Eigen::Vector2d(x, y)); // 存储像素坐标  }  // 估计01~05.png图像的位姿  Sophus::SE3d T_cur_ref; // 当前图像相对于参考图像的位姿  // 遍历01~05.png图像，进行位姿估计  for (int i = 1; i < 6; i++) {  cv::Mat img = cv::imread((fmt_others % i).str(), 0); // 读取图像  // 可以尝试取消注释以下行以使用单层直接法位姿估计  // DirectPoseEstimationSingleLayer(left_img, img, pixels_ref, depth_ref, T_cur_ref);  DirectPoseEstimationMultiLayer(left_img, img, pixels_ref, depth_ref, T_cur_ref); // 使用多层直接法进行位姿估计  }  return 0; // 程序正常退出  
}
// 函数定义，用于直接估计两帧之间的位姿变换  
void DirectPoseEstimationSingleLayer(  const cv::Mat &img1,  // 第一个输入图像  const cv::Mat &img2,  // 第二个输入图像  const VecVector2d &px_ref,  // 参考图像中的像素点坐标  const vector<double> depth_ref,  // 参考图像中对应像素点的深度值  Sophus::SE3d &T21) {  // 输出位姿变换矩阵，从第一帧到第二帧的变换  const int iterations = 10;  // 设定迭代次数为10  double cost = 0, lastCost = 0;  // 初始化当前和上一次迭代的代价值  // 记录开始时间  auto t1 = chrono::steady_clock::now();  // 初始化雅可比累加器，用于计算和优化位姿变换  JacobianAccumulator jaco_accu(img1, img2, px_ref, depth_ref, T21);  // 开始迭代优化过程  for (int iter = 0; iter < iterations; iter++) {  jaco_accu.reset();  // 重置雅可比累加器  // 并行计算每个像素点的雅可比矩阵和偏差  cv::parallel_for_(cv::Range(0, px_ref.size()),  std::bind(&JacobianAccumulator::accumulate_jacobian, &jaco_accu, std::placeholders::_1));  // 获取当前位姿下的海森矩阵和偏差  Matrix6d H = jaco_accu.hessian();  Vector6d b = jaco_accu.bias();  // 使用LDLT分解法求解更新量  Vector6d update = H.ldlt().solve(b);  // 更新位姿变换  T21 = Sophus::SE3d::exp(update) * T21;  // 计算当前位姿下的代价  cost = jaco_accu.cost_func();  // 检查更新量是否为NaN，如果是则中断迭代  if (std::isnan(update[0])) {  cout << "update is nan" << endl;  break;  }  // 如果代价增加，中断迭代  if (iter > 0 && cost > lastCost) {  cout << "cost increased: " << cost << ", " << lastCost << endl;  break;  }  // 如果更新量的范数小于阈值，则认为已经收敛，中断迭代  if (update.norm() < 1e-3) {  break;  }  lastCost = cost;  // 更新上一次迭代的成本  cout << "iteration: " << iter << ", cost: " << cost << endl;  // 输出迭代信息和成本  }  // 输出最终的位姿变换矩阵  cout << "T21 = \n" << T21.matrix() << endl;  // 记录结束时间，并计算运行时间  auto t2 = chrono::steady_clock::now();  auto time_used = chrono::duration_cast<chrono::duration<double>>(t2 - t1);  cout << "direct method for single layer: " << time_used.count() << endl;  // 在图像上显示投影点  cv::Mat img2_show;  cv::cvtColor(img2, img2_show, CV_GRAY2BGR);  VecVector2d projection = jaco_accu.projected_points();  // 获取投影点  // 遍历每个投影点，并在图像上绘制  for (size_t i = 0; i < px_ref.size(); ++i) {  auto p_ref = px_ref[i];  auto p_cur = projection[i];  if (p_cur[0] > 0 && p_cur[1] > 0) {  cv::circle(img2_show, cv::Point2f(p_cur[0], p_cur[1]), 2, cv::Scalar(0, 250, 0), 2);  cv::line(img2_show, cv::Point2f(p_ref[0], p_ref[1]), cv::Point2f(p_cur[0], p_cur[1]),  cv::Scalar(0, 250, 0));  }  }  // 显示并等待用户按键  cv::imshow("current", img2_show);  cv::waitKey();  
}
void JacobianAccumulator::accumulate_jacobian(const cv::Range &range) {  // 定义并初始化一些参数  const int half_patch_size = 1;  // 区块半径  int cnt_good = 0;  // 记录有效点的数量  Matrix6d hessian = Matrix6d::Zero();  // 初始化海森矩阵为0  Vector6d bias = Vector6d::Zero();  // 初始化偏置向量为0  double cost_tmp = 0;  // 初始化临时代价为0  // 遍历给定的范围  for (size_t i = range.start; i < range.end; i++) {  // 通过参考图像中的点计算在当前图像中的投影  Eigen::Vector3d point_ref =  depth_ref[i] * Eigen::Vector3d((px_ref[i][0] - cx) / fx, (px_ref[i][1] - cy) / fy, 1);  Eigen::Vector3d point_cur = T21 * point_ref;  // 使用变换矩阵T21进行变换  if (point_cur[2] < 0)   // 如果深度无效，则跳过此点  continue;  // 计算投影在当前图像中的像素坐标  float u = fx * point_cur[0] / point_cur[2] + cx, v = fy * point_cur[1] / point_cur[2] + cy;  // 如果投影点超出了图像边界，则跳过此点  if (u < half_patch_size || u > img2.cols - half_patch_size || v < half_patch_size ||  v > img2.rows - half_patch_size)  continue;  projection[i] = Eigen::Vector2d(u, v);  // 保存投影点的坐标  // 提取并计算一些中间变量，以提高效率  double X = point_cur[0], Y = point_cur[1], Z = point_cur[2],  Z2 = Z * Z, Z_inv = 1.0 / Z, Z2_inv = Z_inv * Z_inv;  cnt_good++;  // 有效点数量加1  // 在补丁范围内计算误差和雅可比矩阵  for (int x = -half_patch_size; x <= half_patch_size; x++)  for (int y = -half_patch_size; y <= half_patch_size; y++) {  // 计算两个图像在对应位置的像素值之差作为误差  double error = GetPixelValue(img1, px_ref[i][0] + x, px_ref[i][1] + y) -  GetPixelValue(img2, u + x, v + y);  // 初始化像素对相机位姿的雅可比矩阵  Matrix26d J_pixel_xi;  Eigen::Vector2d J_img_pixel;  // 计算J_pixel_xi，即像素坐标对相机位姿的偏导数  // ... (此处省略了具体的偏导数计算过程，代码已直接给出结果)  // 计算图像梯度J_img_pixel，使用中心差分法  J_img_pixel = Eigen::Vector2d(  0.5 * (GetPixelValue(img2, u + 1 + x, v + y) - GetPixelValue(img2, u - 1 + x, v + y)),  0.5 * (GetPixelValue(img2, u + x, v + 1 + y) - GetPixelValue(img2, u + x, v - 1 + y))  );  // 计算总的雅可比矩阵J  Vector6d J = -1.0 * (J_img_pixel.transpose() * J_pixel_xi).transpose();  // 累加海森矩阵和偏置向量，以及计算临时成本  hessian += J * J.transpose();  bias += -error * J;  cost_tmp += error * error;  }  }  // 如果有有效点，则更新全局的海森矩阵、偏置向量和代价值  if (cnt_good) {  unique_lock<mutex> lck(hessian_mutex);  // 使用互斥锁保证线程安全  H += hessian;  // 累加海森矩阵  b += bias;  // 累加偏置向量  cost += cost_tmp / cnt_good;  // 计算平均成本  }  
}
// 函数声明：直接姿态估计多层方法  
// 输入：两个图像(img1, img2)，参考像素坐标(px_ref)，参考深度值(depth_ref)  
// 输出：从第一个图像坐标系到第二个图像坐标系的变换矩阵T21  
void DirectPoseEstimationMultiLayer(  const cv::Mat &img1,         // 第一个输入图像  const cv::Mat &img2,         // 第二个输入图像  const VecVector2d &px_ref,   // 参考像素坐标  const vector<double> depth_ref, // 参考像素对应的深度值  Sophus::SE3d &T21) {        // 输出变换矩阵  // 定义参数  int pyramids = 4;            // 图像金字塔的层数  double pyramid_scale = 0.5;  // 金字塔每一层的缩放比例  double scales[] = {1.0, 0.5, 0.25, 0.125}; // 金字塔每一层的实际缩放系数  // 创建图像金字塔  vector<cv::Mat> pyr1, pyr2;  // 图像金字塔  for (int i = 0; i < pyramids; i++) {  if (i == 0) {  pyr1.push_back(img1);  // 如果是第一层，则直接加入原图  pyr2.push_back(img2);  } else {  cv::Mat img1_pyr, img2_pyr;  // 对前一层图像进行缩放，以构建当前层的图像  cv::resize(pyr1[i - 1], img1_pyr,  cv::Size(pyr1[i - 1].cols * pyramid_scale, pyr1[i - 1].rows * pyramid_scale));  cv::resize(pyr2[i - 1], img2_pyr,  cv::Size(pyr2[i - 1].cols * pyramid_scale, pyr2[i - 1].rows * pyramid_scale));  pyr1.push_back(img1_pyr);  // 将缩放后的图像添加到金字塔中  pyr2.push_back(img2_pyr);  }  }  double fxG = fx, fyG = fy, cxG = cx, cyG = cy;  // 备份原始的相机内参  for (int level = pyramids - 1; level >= 0; level--) {  VecVector2d px_ref_pyr; // 存储当前金字塔层级的参考像素坐标  for (auto &px: px_ref) {  px_ref_pyr.push_back(scales[level] * px);  // 根据缩放系数调整参考像素坐标  }  // 根据金字塔层级调整相机内参  fx = fxG * scales[level];  fy = fyG * scales[level];  cx = cxG * scales[level];  cy = cyG * scales[level];  // 对当前金字塔层级进行直接姿态估计  DirectPoseEstimationSingleLayer(pyr1[level], pyr2[level], px_ref_pyr, depth_ref, T21);  }  
}

注：上述路径需改为绝对路径.

3. 报错解决方案

（1）路径问题

修改2个cpp文件路径如下

  • optical_flow.cpp
string file_1 = "/home/user_name/slambook2/ch8/LK1.png";  // first image
string file_2 = "/home/user_name/slambook2/ch8/LK2.png";  // second image
  • direct_method.cpp
string left_file = "/home/user_name/slambook2/ch8/left.png";
string disparity_file = "/home/user_name/slambook2/ch8/disparity.png";
boost::format fmt_others("/home/user_name/slambook2/ch8/%06d.png");    // other files

（2）opencv4安装

问题1：error: invalid initialization of reference of type ‘const cv::ParallelLoopB

原因1：之前章节安装的是opencv3，而本章运用了一些opencv4中的函数，且CMakeLists.txt中也有find_package(OpenCV 4 REQUIRED)，故直接安装opencv4

解决1：参考：opencv4安装步骤

问题2：error: “CV_GRAY2BGR was not declared in this scope cv::cvtColor(img2，img2_single，CV_GRAY2BGR)”

解决2：将optical_flow.cpp与direct_method.cpp两个文件中的CV_GRAY2BGR 改为 cv::COLOR_GRAY2BGR（注意区分大小写）。Ctrl+f 查找并修改（2个文件共需修改4处）

这篇关于视觉SLAM学习打卡【8-2】-视觉里程计·直接法代码详解的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/879577。

相关文章

JAVA系统中Spring Boot应用程序的配置文件application.yml使用详解

JAVA系统中Spring Boot应用程序的配置文件application.yml使用详解

《JAVA系统中SpringBoot应用程序的配置文件application.yml使用详解》：本文主要介绍JAVA系统中SpringBoot应用程序的配置文件application.yml的... 目录文件路径文件内容解释1. Server 配置2. Spring 配置3. Logging 配置4. Ma
阅读更多...
python实现pdf转word和excel的示例代码

python实现pdf转word和excel的示例代码

《python实现pdf转word和excel的示例代码》本文主要介绍了python实现pdf转word和excel的示例代码,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价... 目录一、引言二、python编程1，PDF转Word2，PDF转Excel三、前端页面效果展示总结一
阅读更多...
在MyBatis的XML映射文件中＜trim＞元素所有场景下的完整使用示例代码

在MyBatis的XML映射文件中＜trim＞元素所有场景下的完整使用示例代码

《在MyBatis的XML映射文件中＜trim＞元素所有场景下的完整使用示例代码》在MyBatis的XML映射文件中,trim元素用于动态添加SQL语句的一部分,处理前缀、后缀及多余的逗号或连接符,示... 在MyBATis的XML映射文件中，<trim>元素用于动态地添加SQL语句的一部分，例如SET或W
阅读更多...
mac中资源库在哪? macOS资源库文件夹详解

mac中资源库在哪? macOS资源库文件夹详解

《mac中资源库在哪?macOS资源库文件夹详解》经常使用Mac电脑的用户会发现，找不到Mac电脑的资源库，我们怎么打开资源库并使用呢？下面我们就来看看macOS资源库文件夹详解... 在 MACOS 系统中，「资源库」文件夹是用来存放操作系统和 App 设置的核心位置。虽然平时我们很少直接跟它打交道，但了
阅读更多...
关于Maven中pom.xml文件配置详解

关于Maven中pom.xml文件配置详解

《关于Maven中pom.xml文件配置详解》pom.xml是Maven项目的核心配置文件,它描述了项目的结构、依赖关系、构建配置等信息,通过合理配置pom.xml,可以提高项目的可维护性和构建效率... 目录1. POM文件的基本结构1.1 项目基本信息2. 项目属性2.1 引用属性3. 项目依赖4. 构
阅读更多...
Rust 数据类型详解

Rust 数据类型详解

《Rust数据类型详解》本文介绍了Rust编程语言中的标量类型和复合类型,标量类型包括整数、浮点数、布尔和字符,而复合类型则包括元组和数组,标量类型用于表示单个值,具有不同的表示和范围,本文介绍的非... 目录一、标量类型（Scalar Types）1. 整数类型（Integer Types）1.1 整数字
阅读更多...
Java操作ElasticSearch的实例详解

Java操作ElasticSearch的实例详解

《Java操作ElasticSearch的实例详解》Elasticsearch是一个分布式的搜索和分析引擎,广泛用于全文搜索、日志分析等场景,本文将介绍如何在Java应用中使用Elastics... 目录简介环境准备1. 安装 Elasticsearch2. 添加依赖连接 Elasticsearch1. 创
阅读更多...
使用C#代码计算数学表达式实例

使用C#代码计算数学表达式实例

《使用C#代码计算数学表达式实例》这段文字主要讲述了如何使用C#语言来计算数学表达式,该程序通过使用Dictionary保存变量,定义了运算符优先级,并实现了EvaluateExpression方法来... 目录C#代码计算数学表达式该方法很长，因此我将分段描述下面的代码片段显示了下一步以下代码显示该方法如
阅读更多...
Redis缓存问题与缓存更新机制详解

Redis缓存问题与缓存更新机制详解

《Redis缓存问题与缓存更新机制详解》本文主要介绍了缓存问题及其解决方案,包括缓存穿透、缓存击穿、缓存雪崩等问题的成因以及相应的预防和解决方法,同时,还详细探讨了缓存更新机制,包括不同情况下的缓存更... 目录一、缓存问题1.1 缓存穿透1.1.1 问题来源1.1.2 解决方案1.2 缓存击穿1.2.1
阅读更多...
PyTorch使用教程之Tensor包详解

PyTorch使用教程之Tensor包详解

《PyTorch使用教程之Tensor包详解》这篇文章介绍了PyTorch中的张量（Tensor）数据结构,包括张量的数据类型、初始化、常用操作、属性等,张量是PyTorch框架中的核心数据结构,支持... 目录1、张量Tensor2、数据类型3、初始化（构造张量）4、常用操作5、常用属性5.1 存储（st
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2