本文主要是介绍最优控制理论笔记 - 01数学准备,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
目录
一、向量和矩阵的微分
1. 向量对标量的导数
2. 矩阵对标量的导数
2.1 矩阵对标量的导数的运算公式
2.2 标量函数对向量的导数:
2.3 向量函数对向量的导数
二、函数极值的问题
三、有约束条件的函数极值问题
四、n元函数的Taylor
一、向量和矩阵的微分
1. 向量对标量的导数
n维向量函数:f(t) = [f1(t), f2(t), ..., fn(t)]T,对标量自变量t的导数定义为:
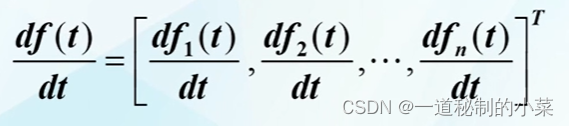
2. 矩阵对标量的导数

2.1 矩阵对标量的导数的运算公式
矩阵对标量的导数的运算公式:

2.2 标量函数对向量的导数:

称为梯度或者偏导数。
2.3 向量函数对向量的导数


二、函数极值的问题


接下来我们对n元进行推广:

三、有约束条件的函数极值问题

推广到n元方程中:

四、n元函数的Taylor



这篇关于最优控制理论笔记 - 01数学准备的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







