本文主要是介绍3.1 词法分析 --- 从正则表达式到非确定有限状态自动机,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
回顾:自动生成
我们想要有一个词法分析器的自动生成器(也就是一个工具)来自动生成这个词法分析器,那么程序员只需要写一个声明式的规范(例如正则表达式),作为一个规范来描述所有词法单元的规则,然后就会有这样的工具来帮我们生成出一个词法分析器出来,它典型的是一个 DFA。

那么这个自动语法生成工具的内部工作流程图下图所示:

RE(正则表达式) -> NFA(非确定的有限自动机) -> DFA(确定的有限状态自动机) --> 算法代码从正则表达式(RE) --> 非确定有限状态自动机(NFA) ==> Thompson 算法非确定有限状态自动机(NFA) -> 确定的有限状态自动机(DFA) ==> 子集构造算法确定的有限状态自动机(DFA) -> 期望它尽可能小和效率尽可能高 ==> Hopcroft 最小化算法这些中间的转换 算法\过程 更像是一个小的编译器,这个编译器接受的输入是 声明式规范(正则表达式) 输出是 转换算法(RE...词法分析器代码)
第一个转换算法:
RE(正则表达式) -> NFA(非确定的有限状态自动机):Thompson 算法
它是基于对RE(正则表达式)的结构做归纳来实现这个算法(类似数学归纳法)
- 对基本的RE直接构造 (2种)
- 对复合的RE做递归构造 (3种)
从实现上来说 它是一个递归算法。在数据结构中,如果一个算法是递归算法,那么往往这样一个算法代码量会比较少,整个结构会比较工整,并且实践相对比较容易。
具体构造过程:
e -> ε ;空转-> c ;单个字符 c-> e1 ;正则表达式的链接-> e1 | e2 ;正则表达式的选择-> e1 * ;正则表达式的预报1.
对 ε 空转:NFA
\ [0] --- ε ---> [[1]]0 号状态是 起始状态,1号状态是接收状态,中间使用 ε 链接。ε 是从0号状态到 1号状态的转换,不需要消耗 S 字符串中的字符,也就是说它是没有代价的2.\[0] --- c ---> [[1]]和上面相同 是直接构造3.递归构造:首先构造e1 e2的表达式:\ 递归 识别e1[0] --- e1 --->[[1]] \ 递归 识别e2[0] --- e2 --->[[1]]
在这里我们想,如果从前面一个 e1 的接受状态可以向下走,走到下一个的起始状态,并且中间链接
一个 ε (空转,不消耗任何字符串) 就可以构造 e1,e2 对应的子表达式的 NFA 由识别 e1 并且链接 e2
\[] --- e1 --->[] ---ε---> [] ---e2--->[[]]
为什么不把自动机化成:
\
[]--e1-->[]--e2-->[[]]
这和自动机等价于上面的 (由识别 e1 并且链接 e2) 自动机
是因为:
上面的算法递归起来更加工整,并且如果去实现算法的话就会发现做节点的融合和边的删除在算法上并不是非常直接4. e1 | e2
首先构造识别 e1 的自动机
\
[] --- e1 ---> [[]]然后构造识别 e2 的自动机
\
[] --- e2 ---> [[]]构造可以识别e1 或者 e2 的自动机:
新增加一个起始节点和一个接受状态的节点,然后链接这几条边就可以

在这里插入代码片
递归 e1 所对应的自动机
\
[1] --- e1 ---> [[2]]构造闭包:
0 个或任意多个 e1 链接到一起0个的概念
在 e1 添加两个状态,一个起始状态一个接受状态,0个是可以不经过 e1,也就是 ε 这
条边由输入直接到达接受状态。
1 个的概念
1.去除掉 1 号节点的输入状态,把输入状态放新添加的状态 0 号节点
2.去掉2号节点接收状态\
[0] ---> [1] --- e1 ---> [2]--->[[3]]
|----------- ε ---------------/2 个的概念
增加 从 2 号 节点 到一号节点的 ε 边,这样可以做一个循环,一直会走一个 e1输入
\ /----- ε ----\
[0] ---> [1] --- e1 ---> [2]--->[[3]]
|----------- ε ---------------/从正则表达式到非确定状态有限自动机示例:
这个例子包含了三种符合形式和一种基本形式,它里面有字符、 正则表达式选择、正则表达式链接、正则表达式闭包
顺序:
括号 — 闭包 — 链接 — 选择
a(b|c)*
做第一步分解:
a(b|c)

第二部分解:我们做正则表达式的闭包:
a(b|c)*

… 部分应该是对应的 b | c

最终的结果:
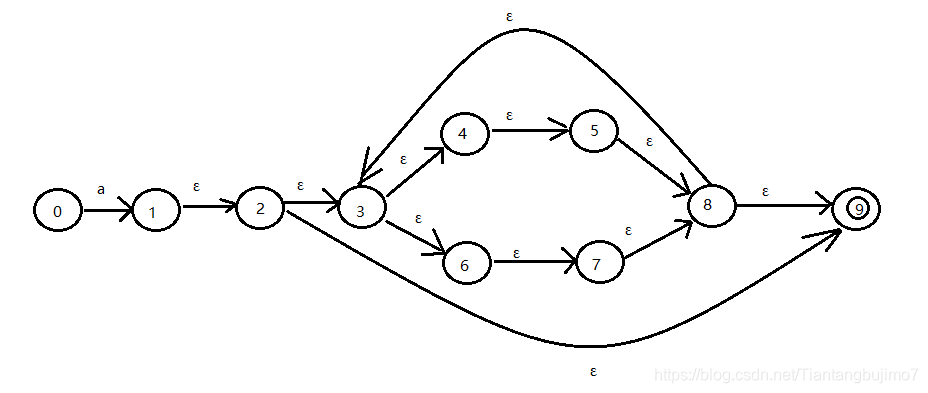
这篇关于3.1 词法分析 --- 从正则表达式到非确定有限状态自动机的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






