红黑树介绍与模拟实现（insert+颜色调整精美图示超详解哦）

2024-04-04 21:28
文章标签 实现 详解 介绍 模拟 红黑树 调整 insert 颜色 图示 精美

本文主要是介绍红黑树介绍与模拟实现（insert+颜色调整精美图示超详解哦），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

红黑树

  • 引言
  • 红黑树的介绍
  • 实现
    • 结点类
    • insert
      • 搜索插入位置
      • 插入
      • 调整
        • 当parent为gparent的左子结点
        • 当parent为gparent的右子结点
  • 参考源码
  • 测试红黑树是否合格
  • 总结

引言

在上一篇文章中我们认识了高度平衡的平衡二叉树AVL树：戳我看AVL树详解哦
（关于旋转调整的部分，在AVL树的时候已经详细介绍过了，如果大家对旋转调平衡的部分有疑惑的话，请移步至AVL树的详解）

由于AVL树的高度平衡，其平均搜索时间复杂度几乎可以达到严格的O(logN)。同样也因为平衡的程度很高，在维护平衡上时间的花费对于搜索上时间的提升是得不偿失的。
大多数情况下，我们并不需要很高的平衡程度，只需要达成一种接近平衡的状态，搜索的平均时间复杂度基本达到O(logN)即可。 红黑树就是这样的一种结构，它的最高子树的高度小于等于最低子树的二倍。通过减少调平衡时的时间成本来提高效率：

红黑树的介绍

红黑树是平衡二叉树的一种，他在满足二叉搜索树特性的基础上，给每个结点增加了一个颜色属性，包括Red与Black；并要求从根节点到一个叶子结点形成的任意一条路径中，通过对结点颜色的限制规则，没有任何一条路径回比其他的路径长一倍：
在这里插入图片描述
（红黑圣诞树）

对于红黑树结点颜色的限制规则如下：

  • 每个结点的颜色只有红色或黑色两种；
  • 根结点的颜色一定是黑色的；
  • 如果某一个结点的颜色是红色的，它的两个孩子结点的颜色一定是黑色（即不存在两个连续的红色结点）；
  • 对于任一结点，到叶子结点的任一路径上，包含的黑色结点的数量一定相等；
  • 叶子结点一定是黑色的（这里的叶子结点直最后的nullptr）

当满足上面的所有规则时，根节点到叶子结点的任一路径就都不可能比其他路径长一倍。由于不存在连续的红色结点，所以当黑色结点的数量 n 一定时，最长路径的长度为2 * n，最短路径的长度为 n ，所以不可能相差一倍以上。这样就达成了一种相对平衡的状态，并不需要经常去旋转调平了。

实现

红黑树的实现，在之前的二叉搜索树上增加了结点的颜色，以及对于结点的颜色调整的部分；
在本篇文章中依旧实现 K-V的模式 的树， 并且以非递归实现insert；
为防止命名冲突，将实现放在我们的命名空间qqq中：

结点的颜色我们使用 枚举常量enum Color 来表示；

RBTree是一个类模板，有两个模板参数，即K与V，表示其中存储的索引类型与值类型；
成员变量类型为Node*（由结点类RBTreeNode重命名），表示根结点的指针：

 //基本的代码结构
namespace qqq
{enum Color //枚举常量表示颜色{RED,BLUCK};template<class K, class V>struct RBTreeNode  //结点类{};template<class K, class V>class RBTree  //红黑树{typedef RBTreeNode<K, V> Node;public:bool insert(const pair<K, V>& kv){}protected:Node* _root = nullptr;};
}

结点类

首先，对红黑树的结点进行实现：

RBTreeNode是也一个类模板， 两个模板参数同样为K与V，表示索引与值的类型；
在结点中储存数据的结构为pair，其中first为K类型，second为V类型；

成员变量包括结点中的数据 _kv；
指向父亲结点的指针 _parent；
指向左右孩子结点的指针 _left 与 _right；
表示结点颜色的枚举常量 _col：

template<class K, class V>
struct RBTreeNode  //结点类
{pair<K, V> _kv;RBTreeNode<K, V>* _parent;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;Color _col;
};

结点类的构造函数
我们需要实现一个默认构造函数：
参数类型为const pair<K, V>，缺省值为一个pair<K, V>的匿名对象；
对于父子结点的指针，在初始化列表中初始化为nullptr即可；
对于结点的颜色，在初始化列表中初始化为RED（要保证每条路上黑色结点的个数相等，就必须初始化为红色）：

	RBTreeNode(const pair<K, V> kv = pair<K, V>()): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}

insert

红黑树的insert分为两个部分，即搜索并插入以及调整使其满足红黑树的性质：

搜索插入位置

  • 与二叉搜索树类似，搜索并插入时，首先用要插入的pair对象创建一个新结点newnode；
  • 与此同时，使用结点指针 cur来记录当前位置 ，parent来记录cur的父结点，便于后面插入；
  • 然后 while循环向下查找 插入的位置：当newnode小于cur的元素时，向左查找，当newnode大于cur的元素时，向右查找，相等时即该元素已经存在，返回false；
  • 当cur为nullptr时，表示找到了插入的位置，循环终止：
// 部分代码：搜索插入位置 //
Node* newnode = new Node(kv);
Node* parent = nullptr;
Node* cur = _root;while (cur != nullptr) //搜索
{if (newnode->_kv.first > cur->_kv.first){parent = cur;cur = parent->_right;}else if (newnode->_kv.first < cur->_kv.first){parent = cur;cur = parent->_left;}else  //相等即插入失败{return false;}
}

插入

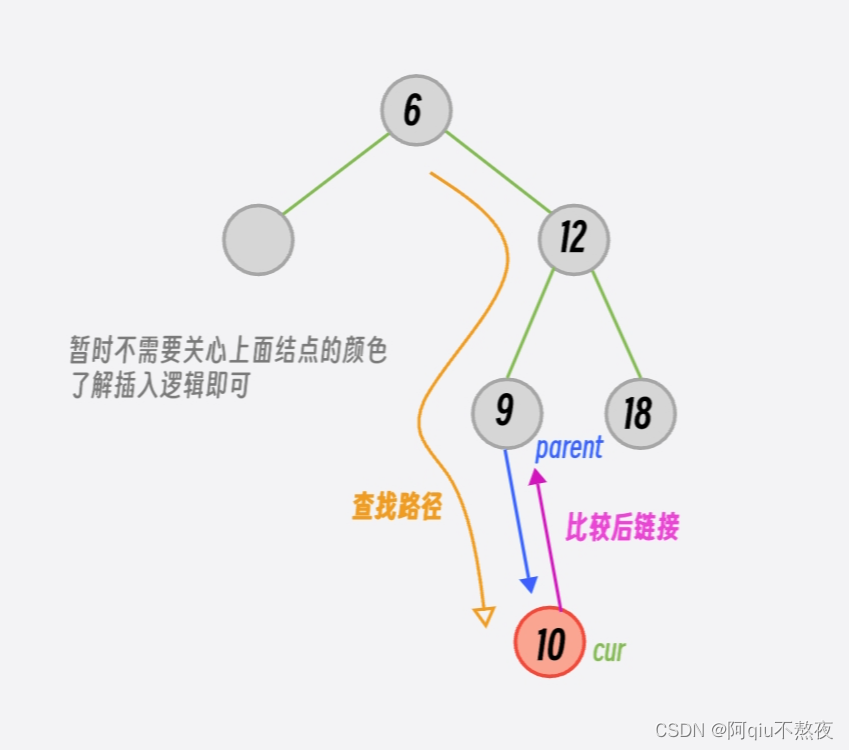
  • 将newnode插入红黑树即将newnode与parent链接，这时就需要判断parent是否为空；
  • 当parent为空时，即cur就是根节点_root，即newnode是这棵红黑树中的第一个结点，将 其赋值给_root 即可；
  • 当parent不为空时， 还需要判断cur位于parent的左边还是右边，然后再插入：

在这里插入图片描述

//  局部代码：插入newnode //
if (parent == nullptr) //插入
{_root = newnode;
}
else if (newnode->_kv.first < parent->_kv.first)
{parent->_left = newnode;newnode->_parent = parent;cur = newnode;
}
else
{parent->_right = newnode;newnode->_parent = parent;cur = newnode;
}

调整

在完成插入后，首先需要判断的是parent指针的状态：

  • 当parent为空时，表明当前结点为根结点，将其颜色改为BLACK即可调整完毕；
  • 当parent指向结点的颜色为BLACK 时，如果是在刚插入时，新插入的结点颜色为RED，不会影响该路径的黑色节点个数，所以不再需要调整。如果是在向上调整的过程中parent指向的结点为BLACK，也意味着整棵树调整结束了（这一点在后面的调整部分会详细介绍）；
  • 除了上面不用调整的两种情况外，其余的情况，即 parent指向的结点存在且为RED 的情况就需要进行调整了。调整是自下而上的，循环向上调整，直到 parent为空或parent指向的结点为BLACK时循环结束，调整完成
// 部分代码：自下而上调整的循环框架 //
while (parent != nullptr && parent->_col != BLUCK) 
{}

开始调整时首先对parent为gparent（cur的祖父结点）的左子结点还是右子结点做一分类讨论（当parent不为黑时，由于根结点必须为黑，所以parent不是根结点，所以gparent一定存在）：

当parent为gparent的左子结点

当parent为gparent的左子结点时，我们首先要考察cur叔叔结点的情况：

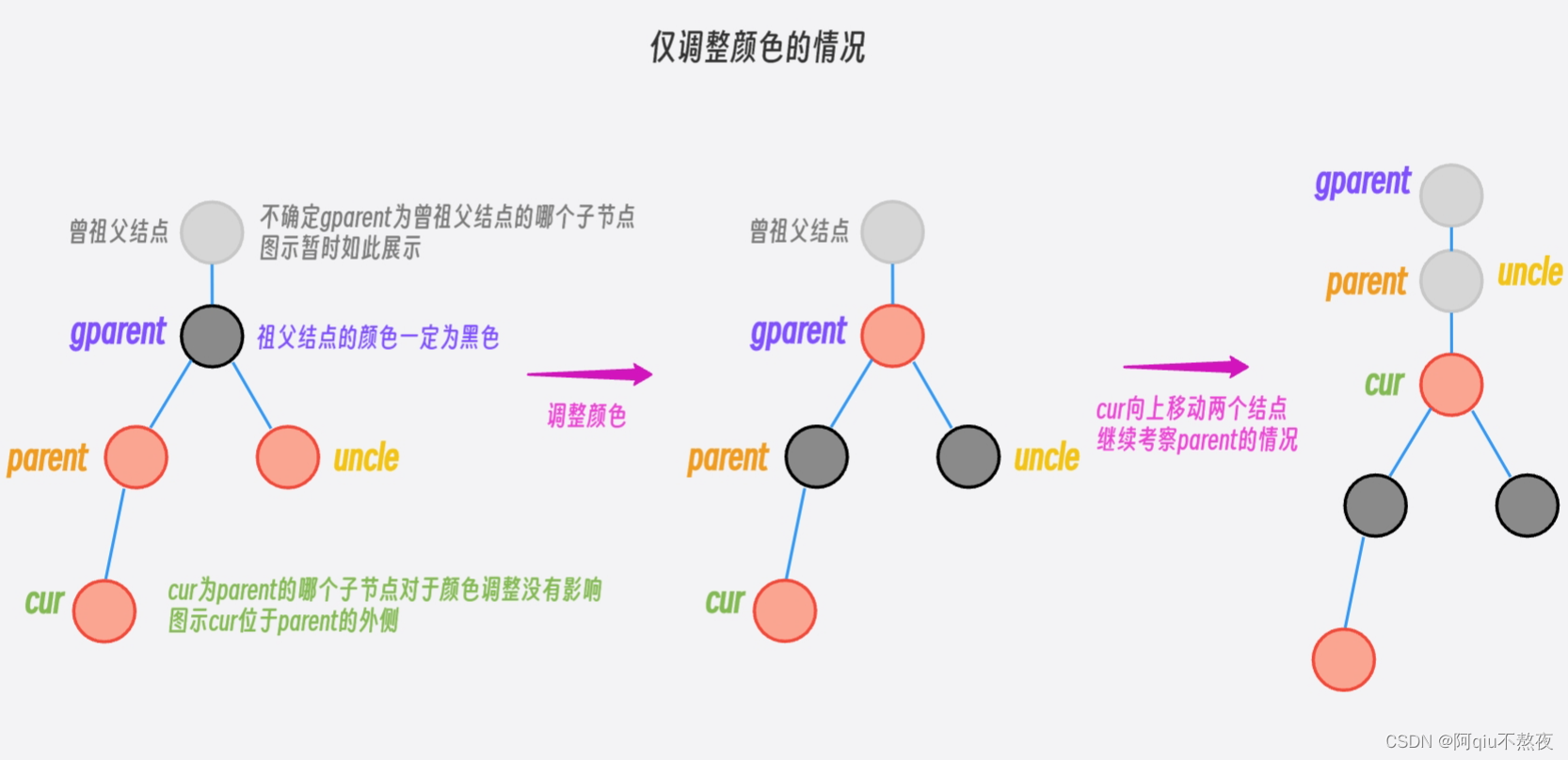
  • 当cur的叔叔结点为RED 时，不需要进行旋转调整，只需要将gparent指向结点设置为RED，将parent和cur的叔叔结点全部设置为BLACK即可：
    由于在调整完颜色后，gparent指向结点颜色就为RED了，这时如果gparent父结点的颜色正好为红，就出现了连续的两个红色结点。所以需要将cur向上移动两个结点，再对其parent指向的结点继续进行判断：
    在这里插入图片描述

  • 当cur的叔叔结点为BLACK或不存在时，就需要进行旋转调整了：
    旋转的逻辑与之前AVL树类似，当cur位于parent的左边时，即左左——单次右旋：
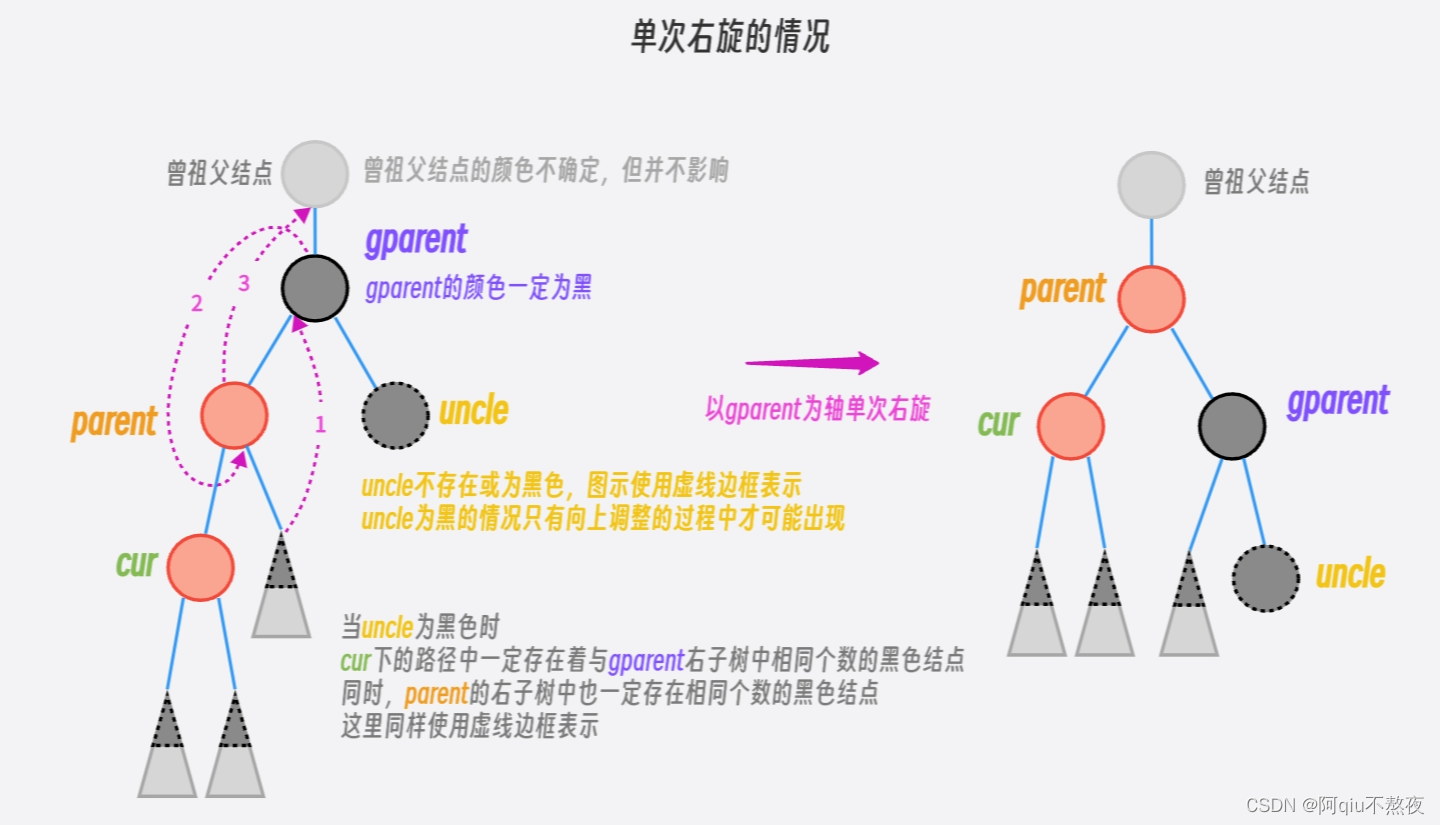
    在这里插入图片描述
    当cur位于parent的右边时，即左右——左右双旋：
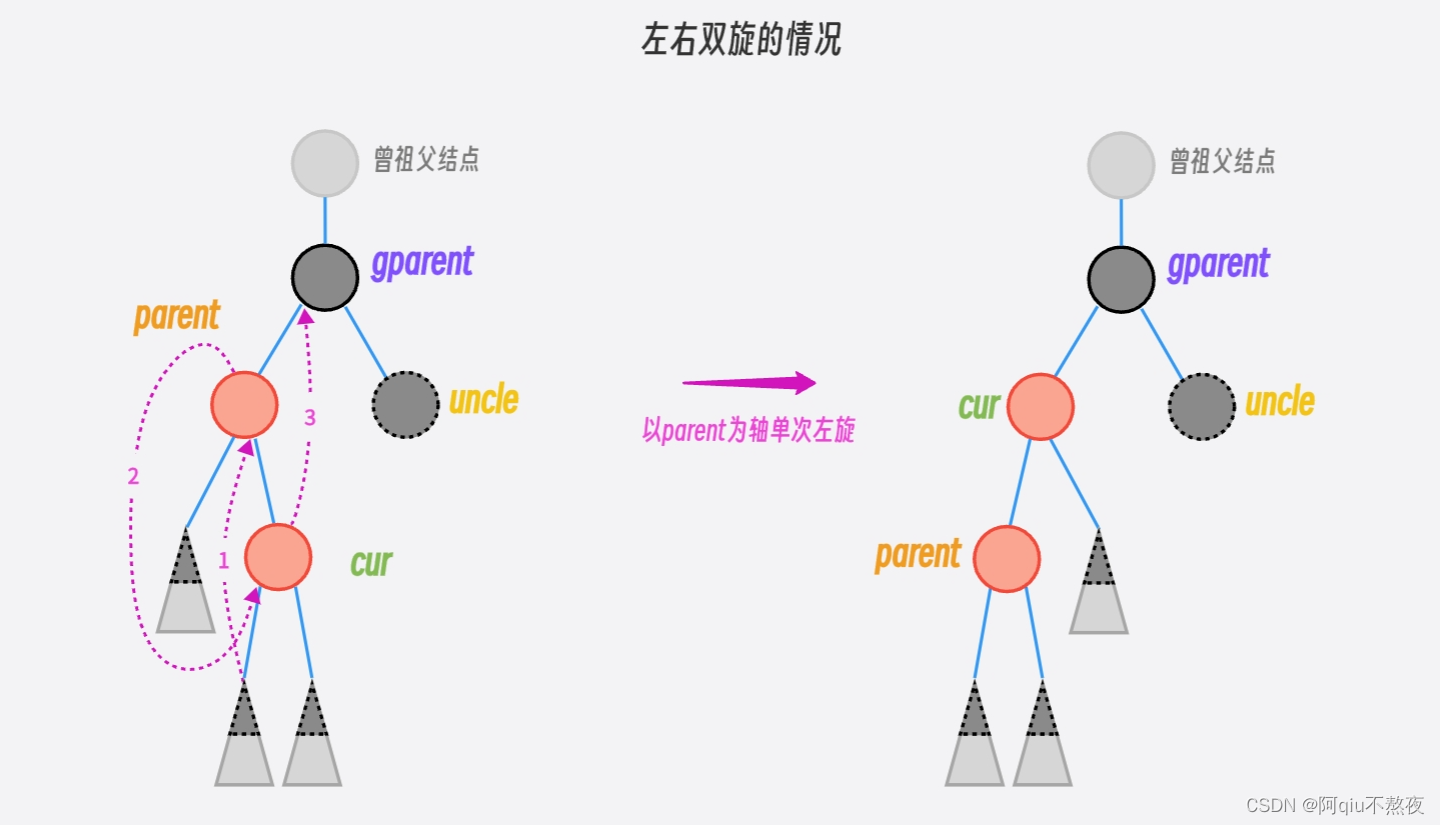
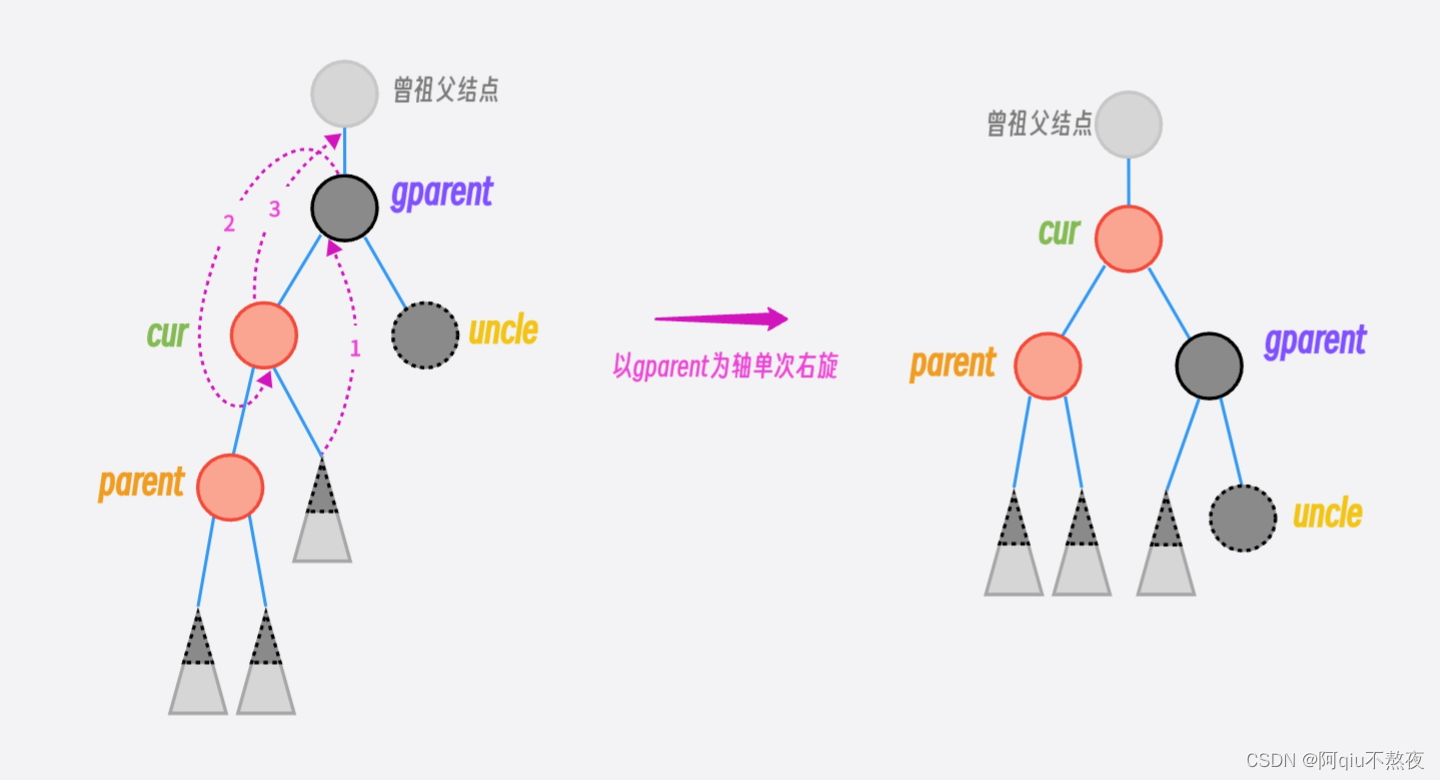
    在这里插入图片描述
    在这里插入图片描述
    旋转调整后将gparent指向结点设置为RED，将子树顶部的结点设置为BLACK 即可（parent指向的结点或cur指向的结点）：
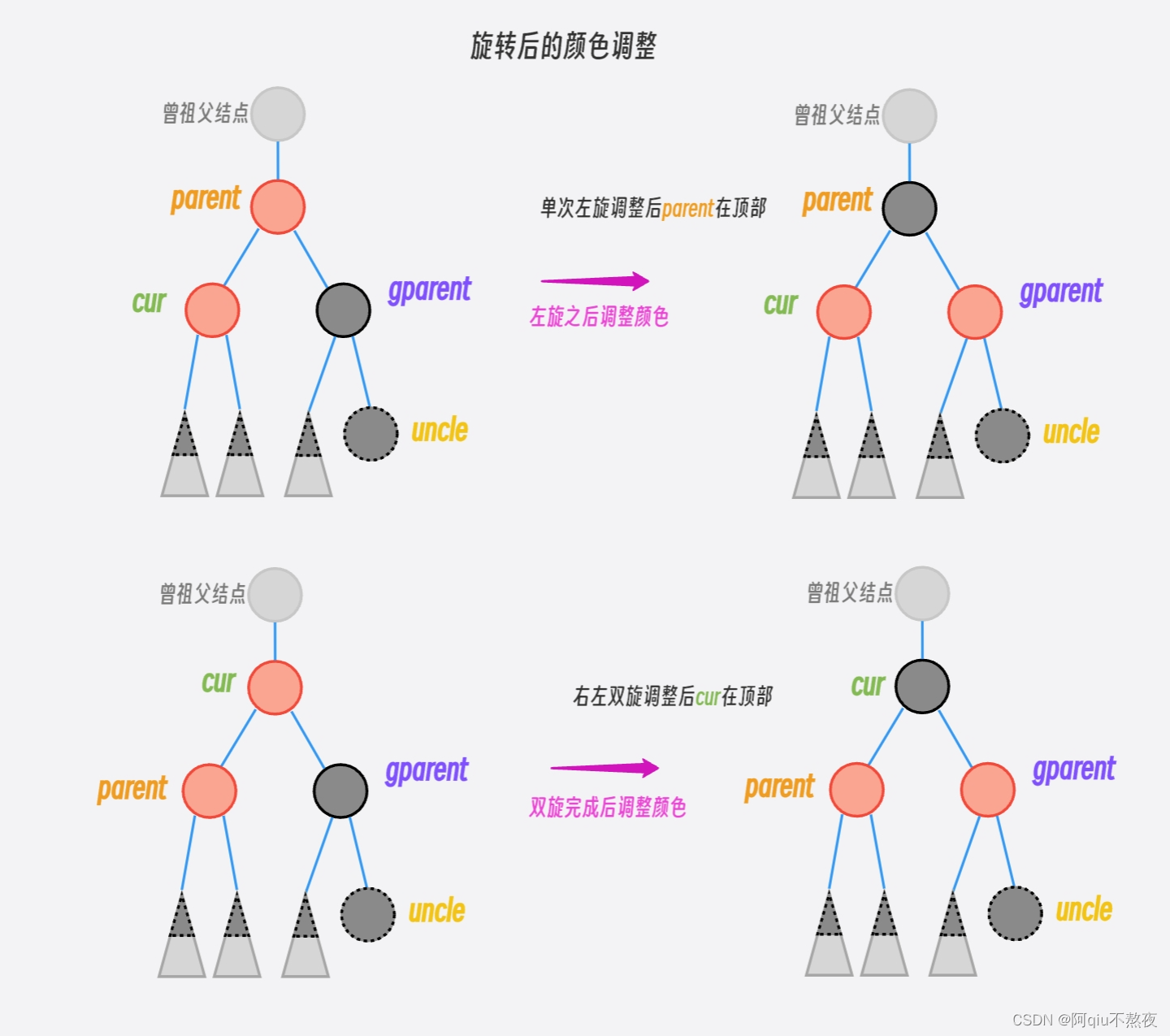
    在这里插入图片描述

经过旋转后的红黑树，子树顶部的颜色一定为黑色，再向上也就不会存在两个连续的红色结点的问题了，所以旋转之后直接终止循环即可。

需要注意的是：叔叔是黑色结点的情况一定是出现在调整过程中发生的，当叔叔结点为黑色时，cur下的路径中一定存在着与gparent右子树中黑色结点相同个数的黑色结点，parent下的路径中同样也存在着相同数目的黑色结点，这样在旋转调平衡后，这棵子树中的所有路径中的黑色结点数目与之前是不变的。

//部分代码：当parent为gparent左子结点的情况
if (parent == gparent->_left)   
{if (gparent->_right == nullptr || gparent->_right->_col == BLUCK)  //1.叔叔结点不存在或为黑，需要旋转并调色{if (cur == parent->_left)//左左->单次右旋{RotateR(gparent);parent->_col = BLUCK;gparent->_col = RED;}else//左右->左旋+右旋{RotateL(parent);RotateR(gparent);cur->_col = BLUCK;gparent->_col = RED;}break; //通过旋转调整后，该子树的根结点一定是黑，所以可以直接结束循环}else if (gparent->_right->_col == RED)  //2.叔叔结点为红，通过调色即可实现红黑树{//调色parent->_col = BLUCK;gparent->_right->_col = BLUCK;gparent->_col = RED;//继续向上cur = gparent;parent = cur->_parent;}else{assert(0);}
}
当parent为gparent的右子结点

当parent为gparent的右子结点时，与上面的情况一致，只是左右对调了，所以这里只给出图示与代码（如果在这种情况下遇到了问题，希望你在上面的情况中能够找到答案）：

  • 叔叔结点为RED，仅调整颜色：
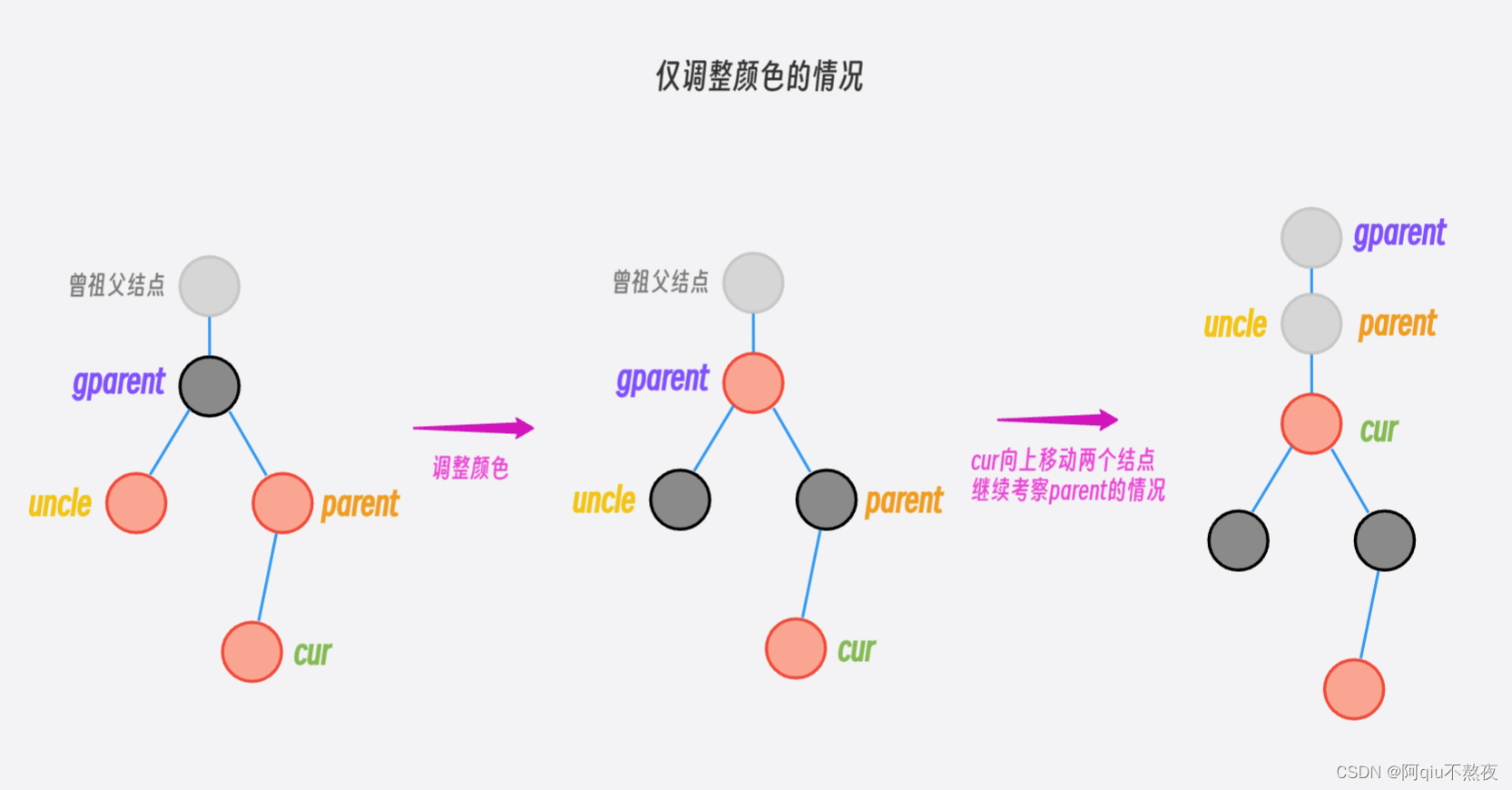
    在这里插入图片描述

  • 叔叔结点为BLACK或不存在，左单旋或右左双旋:
    左单旋：
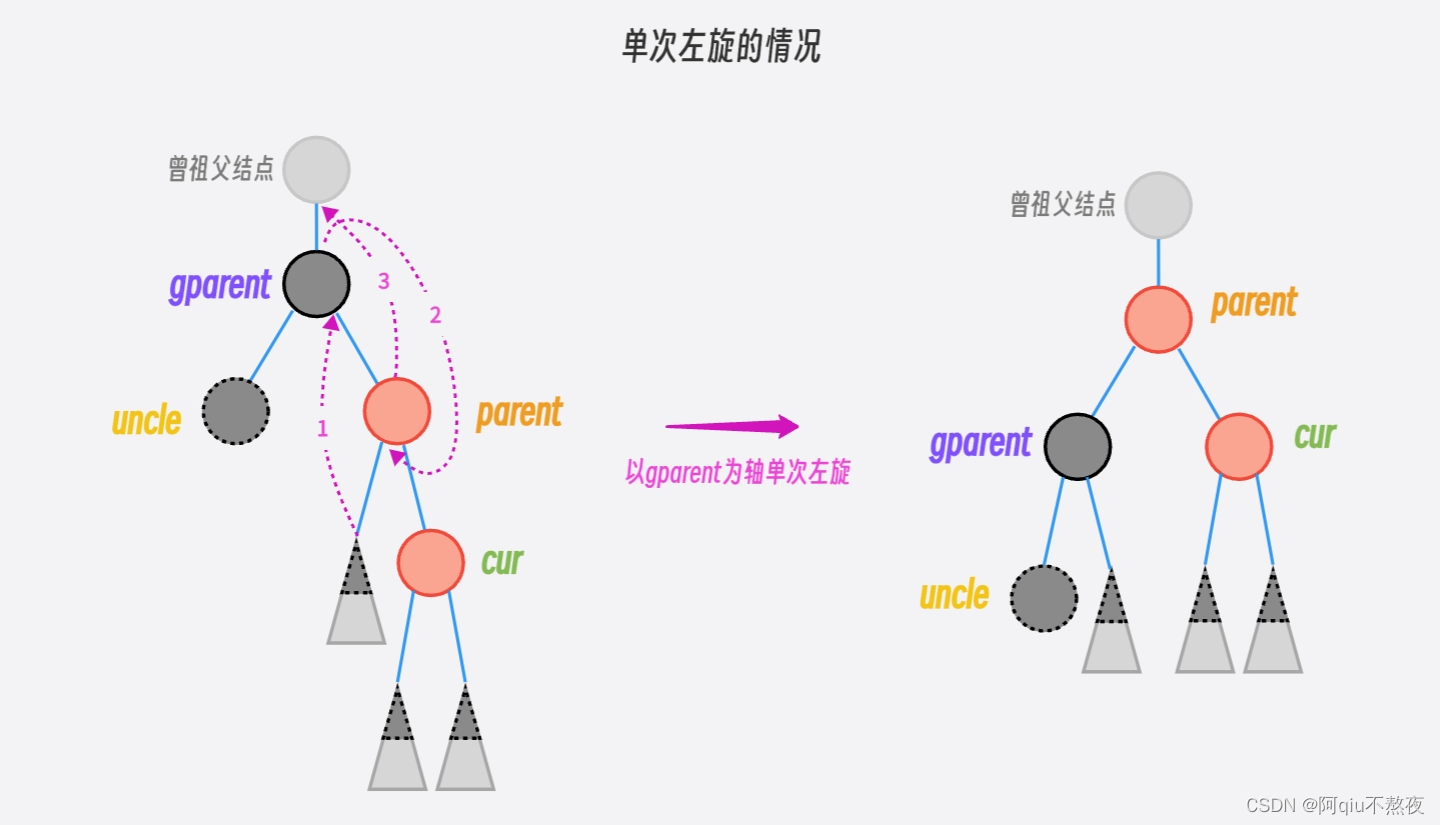
    在这里插入图片描述
    右左双旋：
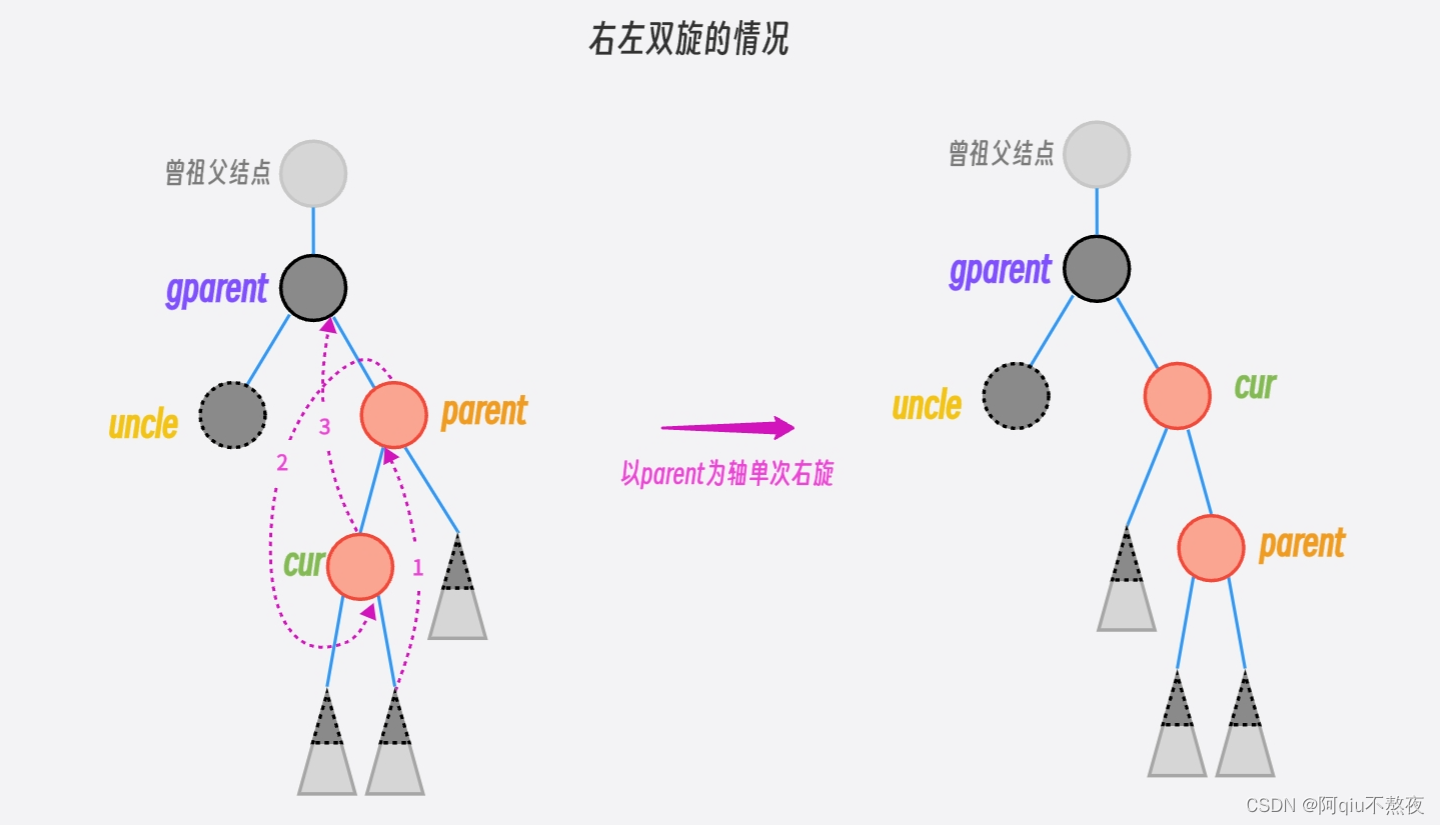
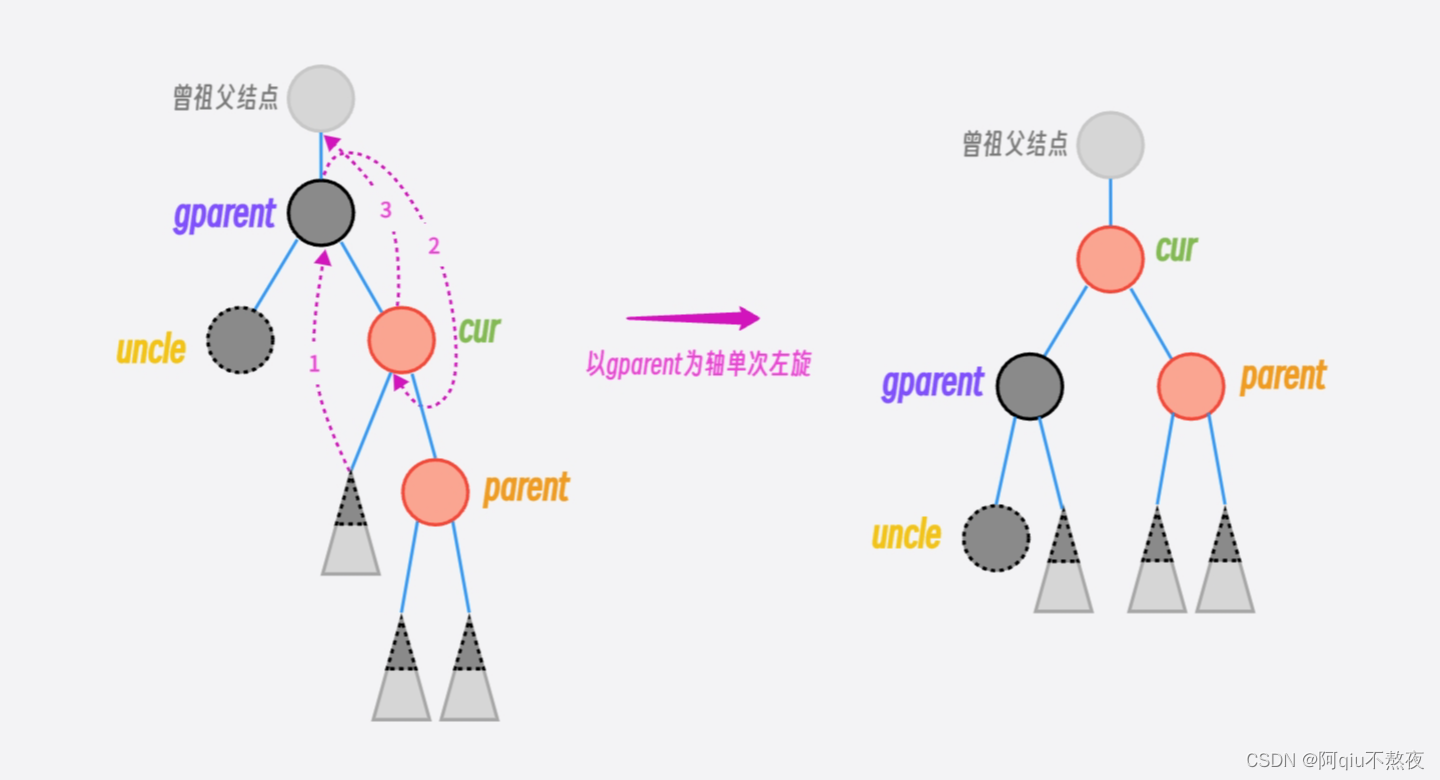
    在这里插入图片描述在这里插入图片描述
    旋转后调整颜色：
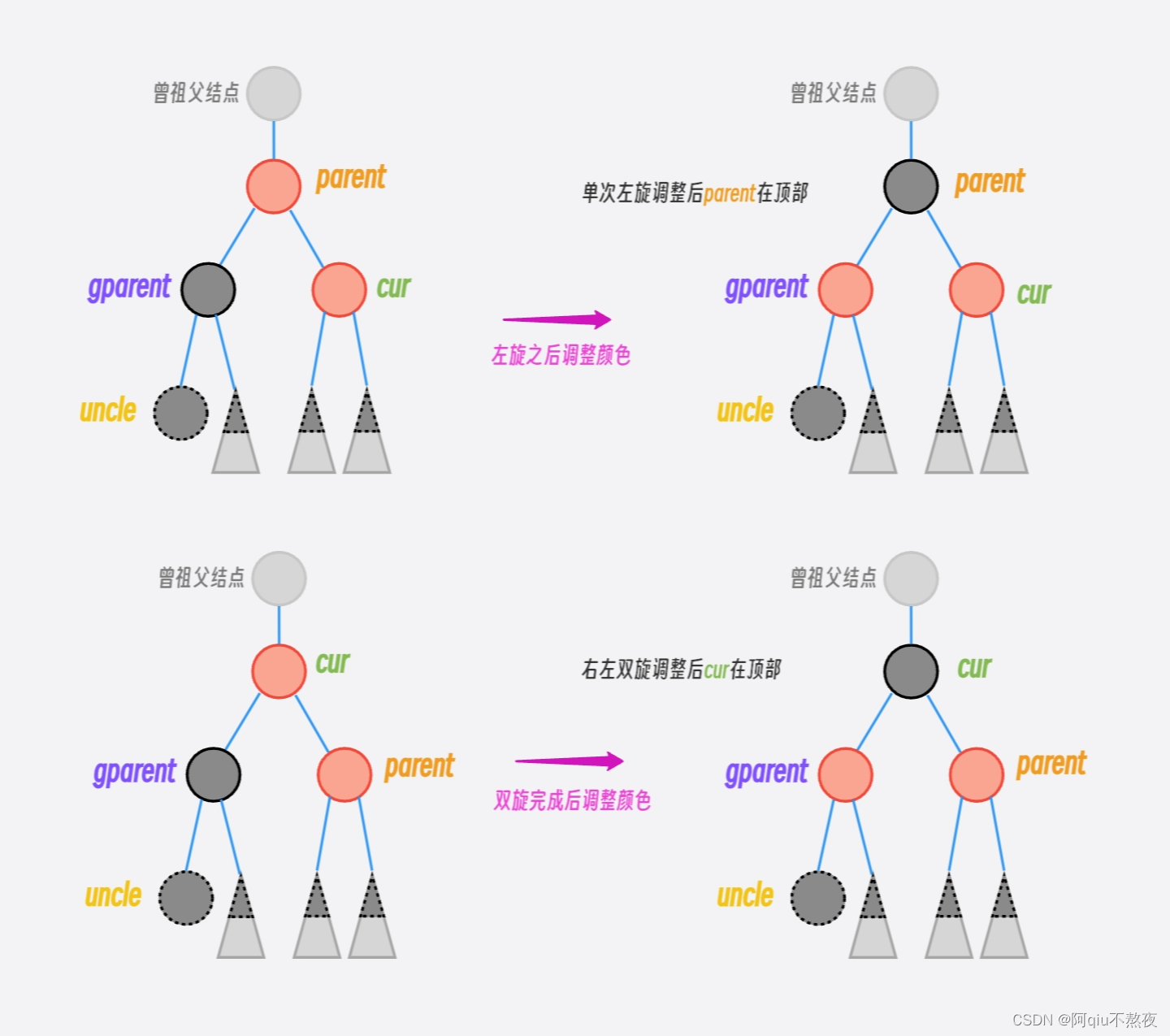
    在这里插入图片描述

旋转后子树顶部的结点一定为BLACK，所以直接break即可。

//部分代码：当parent为gparent右子结点的情况 //
else //parent == gparent->_right
{if (gparent->_left == nullptr || gparent->_left->_col == BLUCK)  //1.叔叔结点不存在或为黑，需要旋转并调色{if (cur == parent->_right)//右右->单次左旋{RotateL(gparent);parent->_col = BLUCK;gparent->_col = RED;}else//右左->右旋+左旋{RotateR(parent);RotateL(gparent);cur->_col = BLUCK;gparent->_col = RED;}break; //通过旋转调整后，该子树的根结点一定是黑，所以可以直接结束循环}else if (gparent->_left->_col == RED)  //2.叔叔结点为红，通过调色即可实现红黑树{//调色parent->_col = BLUCK;gparent->_left->_col = BLUCK;gparent->_col = RED;//继续向上cur = gparent;parent = cur->_parent;}else{assert(0);}
}

在while循环调整结束之后，再将根结点_root的颜色改为BLACK，统一做处理（insert的整体代码在这里就不做展示了，大家跳转至参考源码部分查看即可）。

参考源码

namespace qqq
{enum Color //枚举常量表示颜色{RED,BLUCK};template<class K, class V>struct RBTreeNode  //结点类{pair<K, V> _kv;RBTreeNode<K, V>* _parent;RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;Color _col;RBTreeNode(const pair<K, V> kv = pair<K, V>()): _kv(kv), _left(nullptr), _right(nullptr), _parent(nullptr), _col(RED){}};template<class K, class V>class RBTree  //红黑树{typedef RBTreeNode<K, V> Node;public:bool insert(const pair<K, V>& kv){ //先插入Node* newnode = new Node(kv);Node* parent = nullptr;Node* cur = _root;while (cur != nullptr) //搜索{if (newnode->_kv.first > cur->_kv.first){parent = cur;cur = parent->_right;}else if (newnode->_kv.first < cur->_kv.first){parent = cur;cur = parent->_left;}else  //相等即插入失败{return false;}}if (parent == nullptr) //插入{_root = newnode;}else if (newnode->_kv.first < parent->_kv.first){parent->_left = newnode;newnode->_parent = parent;cur = newnode;}else{parent->_right = newnode;newnode->_parent = parent;cur = newnode;}//调整颜色以及旋转使满足红黑树while (parent != nullptr && parent->_col != BLUCK) //当parent不为黑时，由于根结点必须为黑，所以parent不是根结点，所以gparent一定存在{Node* gparent = parent->_parent;if (parent == gparent->_left)   {if (gparent->_right == nullptr || gparent->_right->_col == BLUCK)  //1.叔叔结点不存在或为黑，需要旋转并调色{if (cur == parent->_left)//左左->单次右旋{RotateR(gparent);parent->_col = BLUCK;gparent->_col = RED;}else//左右->左旋+右旋{RotateL(parent);RotateR(gparent);cur->_col = BLUCK;gparent->_col = RED;}break; //通过旋转调整后，该子树的根结点一定是黑，所以可以直接结束循环}else if (gparent->_right->_col == RED)  //2.叔叔结点为红，通过调色即可实现红黑树{//调色parent->_col = BLUCK;gparent->_right->_col = BLUCK;gparent->_col = RED;//继续向上cur = gparent;parent = cur->_parent;}else{assert(0);}}else{if (gparent->_left == nullptr || gparent->_left->_col == BLUCK)  //1.叔叔结点不存在或为黑，需要旋转并调色{if (cur == parent->_right)//右右->单次左旋{RotateL(gparent);parent->_col = BLUCK;gparent->_col = RED;}else//右左->右旋+左旋{RotateR(parent);RotateL(gparent);cur->_col = BLUCK;gparent->_col = RED;}break; //通过旋转调整后，该子树的根结点一定是黑，所以可以直接结束循环}else if (gparent->_left->_col == RED)  //2.叔叔结点为红，通过调色即可实现红黑树{//调色parent->_col = BLUCK;gparent->_left->_col = BLUCK;gparent->_col = RED;//继续向上cur = gparent;parent = cur->_parent;}else{assert(0);}}}_root->_col = BLUCK;return true;}void RotateL(Node* parent){Node* gparent = parent->_parent;Node* cur = parent->_right;Node* curleft = cur->_left;parent->_right = curleft;if (curleft != nullptr){curleft->_parent = parent;}cur->_left = parent;parent->_parent = cur;cur->_parent = gparent;if (gparent == nullptr){_root = cur;}else{if (cur->_kv.first < gparent->_kv.first){gparent->_left = cur;}else{gparent->_right = cur;}}}void RotateR(Node* parent){Node* gparent = parent->_parent;Node* cur = parent->_left;Node* curright = cur->_right;parent->_left = curright;if (curright != nullptr){curright->_parent = parent;}cur->_right = parent;parent->_parent = cur;cur->_parent = gparent;if (gparent == nullptr){_root = cur;}else{if (cur->_kv.first < gparent->_kv.first){gparent->_left = cur;}else{gparent->_right = cur;}}}bool isRBTree(){return isRBTree(_root);}protected:Node* _root = nullptr;bool checkColor(Node* root, int countBluck, int& baseBluck) //计算黑结点数量与红结点连续是否满足条件{if (root == nullptr){if (baseBluck == countBluck){return true;}return false;}if (root->_col == RED && root->_parent != nullptr && root->_parent->_col == RED){return false;}if (root->_col == BLUCK){countBluck++;}return checkColor(root->_left, countBluck, baseBluck) && checkColor(root->_right, countBluck, baseBluck);}bool isRBTree(Node* root){if (root == nullptr)return true;if (root->_col == RED)return false;//先计算一条路径中的黑色结点数量int baseBluck = 0;Node* cur = root;while (cur != nullptr){if (cur->_col == BLUCK){++baseBluck;}cur = cur->_right;}return checkColor(root, 0, baseBluck);}};
}

测试红黑树是否合格

在写完红黑树的insert之后，我们可以再编写一个测试模块来测试一棵树是否满足红黑树的特性：

我们其实只需要判断两点即可：

  • 任一路径上的黑色结点个数是否相等；
  • 是否存在连续的两个红色结点。

我们使用递归的方式来判断：

判断任一路径上的黑色结点个数是否相等时，必须要先计算某条路径上的黑色结点个数，可以通过 while循环计算最右侧一条路径上的黑色结点个数。将cur从_root开始一直向右子节点遍历即可，当cur为空时即该路径结束，终止循环。

然后使用checkColor函数（参数为当前结点指针Node*，计算中的当前路径黑色结点个数int，以及先前计算的最外层黑色结点个数int ）递归计算每条路径上的黑色结点个数，顺便判断是否存在连续的红色结点。
在递归过程中：
当_root为空时，即当前路径已经结束，判断countBluck与baseBlack的值是否相等，若相等返回true，否则返回false；
若当前结点为红色，则判断其父结点是否为红色，是就返回false；
若当前结点为黑色，countBluck加1，并继续向左右子结点递归，返回左子结点的结果&&右子结点的结果:
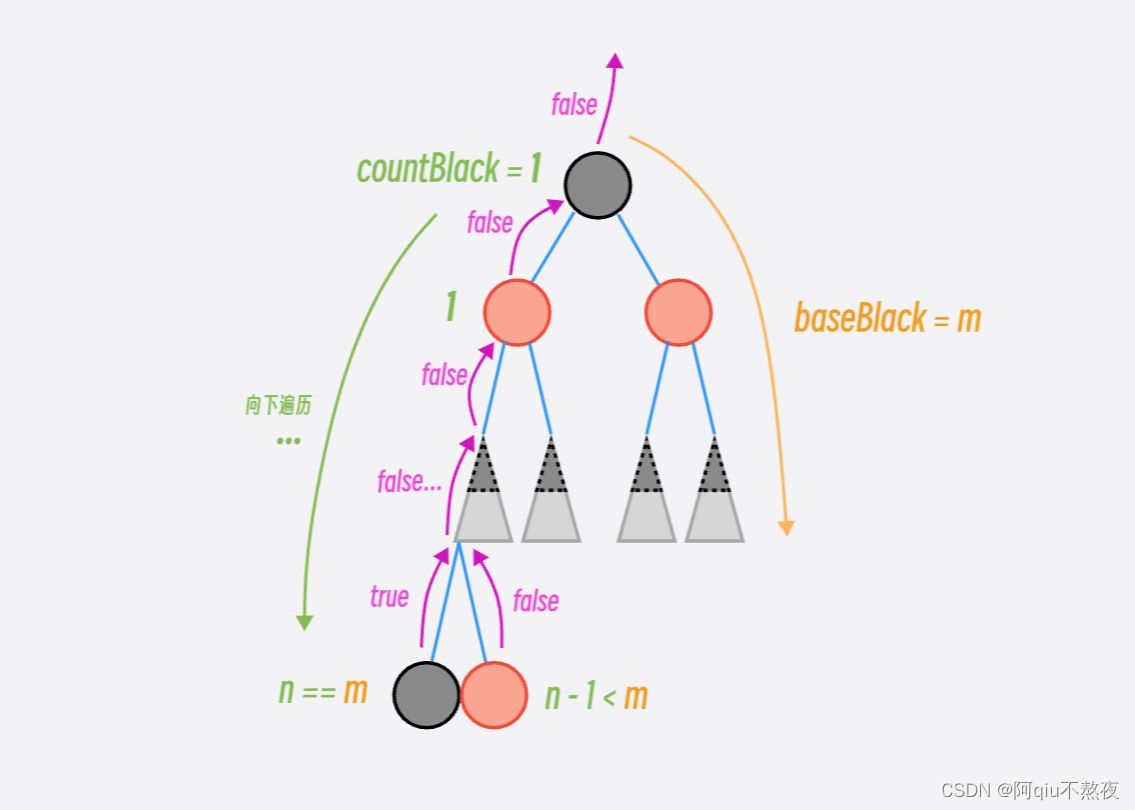
在这里插入图片描述

测试红黑树是否合格的代码这里就不赘述了，大家可以在参考源码部分查找。这里来展示一下测试结果：

namespace qqq
{void testfunc(){const int N = 10000000;vector<int> v;v.reserve(N);srand(time(0));for (size_t i = 0; i < N; i++){v.push_back(i);}RBTree<int, int> rbt;for (auto e : v){rbt.insert(make_pair(e, e));cout << "insert:" << e << "->" << rbt.isRBTree() << endl;}cout << rbt.isRBTree() << endl;}
}int main()
{qqq::testfunc();return 0;
}

在这里插入图片描述
因为这段测试代码中，存在大量I/O，所以运行速度很慢，大家可以将cout注释掉，只打印最后的结果。

总结

到此，关于红黑树的知识就介绍完了
在接下来的文章中，将会对红黑树进行封装，即map与set，尽情期待哦

如果大家认为我对某一部分没有介绍清楚或者某一部分出了问题，欢迎大家在评论区提出

如果本文对你有帮助，希望一键三连哦

希望与大家共同进步哦

这篇关于红黑树介绍与模拟实现（insert+颜色调整精美图示超详解哦）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/876864。

相关文章

python使用watchdog实现文件资源监控

python使用watchdog实现文件资源监控

《python使用watchdog实现文件资源监控》watchdog支持跨平台文件资源监控,可以检测指定文件夹下文件及文件夹变动,下面我们来看看Python如何使用watchdog实现文件资源监控吧... python文件监控库watchdogs简介随着Python在各种应用领域中的广泛使用，其生态环境也
阅读更多...
el-select下拉选择缓存的实现

el-select下拉选择缓存的实现

《el-select下拉选择缓存的实现》本文主要介绍了在使用el-select实现下拉选择缓存时遇到的问题及解决方案,文中通过示例代码介绍的非常详细,对大家的学习或者工作具有一定的参考学习价值,需要的... 目录项目场景：问题描述解决方案：项目场景：从左侧列表中选取字段填入右侧下拉多选框，用户可以对右侧
阅读更多...
Mysql 中的多表连接和连接类型详解

Mysql 中的多表连接和连接类型详解

《Mysql中的多表连接和连接类型详解》这篇文章详细介绍了MySQL中的多表连接及其各种类型,包括内连接、左连接、右连接、全外连接、自连接和交叉连接,通过这些连接方式,可以将分散在不同表中的相关数据... 目录什么是多表连接？1. 内连接（INNER JOIN）2. 左连接（LEFT JOIN 或 LEFT
阅读更多...
Java中switch-case结构的使用方法举例详解

Java中switch-case结构的使用方法举例详解

《Java中switch-case结构的使用方法举例详解》：本文主要介绍Java中switch-case结构使用的相关资料,switch-case结构是Java中处理多个分支条件的一种有效方式,它... 目录前言一、switch-case结构的基本语法二、使用示例三、注意事项四、总结前言对于Java初学者
阅读更多...
Linux内核之内核裁剪详解

Linux内核之内核裁剪详解

《Linux内核之内核裁剪详解》Linux内核裁剪是通过移除不必要的功能和模块,调整配置参数来优化内核,以满足特定需求,裁剪的方法包括使用配置选项、模块化设计和优化配置参数,图形裁剪工具如makeme... 目录简介一、 裁剪的原因二、裁剪的方法三、图形裁剪工具四、操作说明五、make menuconfig
阅读更多...
Python pyinstaller实现图形化打包工具

Python pyinstaller实现图形化打包工具

《Pythonpyinstaller实现图形化打包工具》：本文主要介绍一个使用PythonPYQT5制作的关于pyinstaller打包工具,代替传统的cmd黑窗口模式打包页面,实现更快捷方便的... 目录1.简介2.运行效果3.相关源码1.简介一个使用python PYQT5制作的关于pyinstall
阅读更多...
使用Python实现大文件切片上传及断点续传的方法

使用Python实现大文件切片上传及断点续传的方法

《使用Python实现大文件切片上传及断点续传的方法》本文介绍了使用Python实现大文件切片上传及断点续传的方法,包括功能模块划分（获取上传文件接口状态、临时文件夹状态信息、切片上传、切片合并）、整... 目录概要整体架构流程技术细节获取上传文件状态接口获取临时文件夹状态信息接口切片上传功能文件合并功能小
阅读更多...
python实现自动登录12306自动抢票功能

python实现自动登录12306自动抢票功能

《python实现自动登录12306自动抢票功能》随着互联网技术的发展,越来越多的人选择通过网络平台购票,特别是在中国,12306作为官方火车票预订平台,承担了巨大的访问量,对于热门线路或者节假日出行... 目录一、遇到的问题？二、改进三、进阶–展望总结一、遇到的问题？1.url-正确的表头：就是首先ur
阅读更多...
C#实现文件读写到SQLite数据库

C#实现文件读写到SQLite数据库

《C#实现文件读写到SQLite数据库》这篇文章主要为大家详细介绍了使用C#将文件读写到SQLite数据库的几种方法,文中的示例代码讲解详细,感兴趣的小伙伴可以参考一下... 目录1. 使用 BLOB 存储文件2. 存储文件路径3. 分块存储文件《文件读写到SQLite数据库China编程的方法》博客中，介绍了文
阅读更多...
Redis主从复制实现原理分析

Redis主从复制实现原理分析

《Redis主从复制实现原理分析》Redis主从复制通过Sync和CommandPropagate阶段实现数据同步,2.8版本后引入Psync指令,根据复制偏移量进行全量或部分同步,优化了数据传输效率... 目录Redis主DodMIK从复制实现原理实现原理Psync: 2.8版本后总结Redis主从复制实
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2