代码随想录算法训练营第二十九天（回溯5）|491. 非递减子序列、46. 全排列、47. 全排列 II(JAVA)

本文主要是介绍代码随想录算法训练营第二十九天（回溯5）|491. 非递减子序列、46. 全排列、47. 全排列 II(JAVA)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

---

491. 非递减子序列

给你一个整数数组 nums ，找出并返回所有该数组中不同的递增子序列，递增子序列中 至少有两个元素 。你可以按 任意顺序 返回答案。

数组中可能含有重复元素，如出现两个整数相等，也可以视作递增序列的一种特殊情况。

示例 1：

• 输入：nums = [4,6,7,7]
• 输出：[[4,6],[4,6,7],[4,6,7,7],[4,7],[4,7,7],[6,7],[6,7,7],[7,7]]

示例 2：

• 输入：nums = [4,4,3,2,1]
• 输出：[[4,4]]

提示：

• 1 <= nums.length <= 15
• -100 <= nums[i] <= 100

解题思路

跟之前的子集II很像，但是不能用它的去重逻辑，本题求自增子序列，是不能对原数组进行排序的，排完序的数组都是自增子序列了。

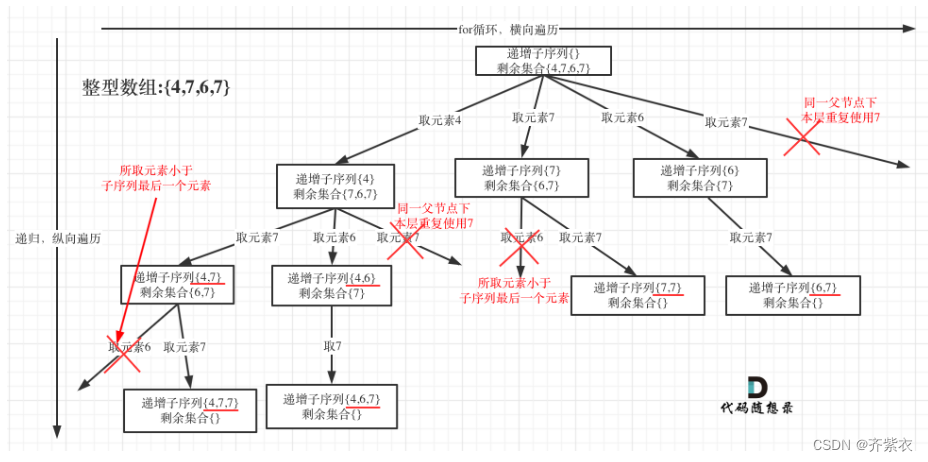
源码

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> findSubsequences(int[] nums) {backTracking(nums, 0);return result;}private void backTracking(int[] nums, int startIndex){if(path.size() >= 2)result.add(new ArrayList<>(path));            HashSet<Integer> hs = new HashSet<>();for(int i = startIndex; i < nums.length; i++){if(!path.isEmpty() && path.get(path.size() -1 ) > nums[i] || hs.contains(nums[i]))continue;hs.add(nums[i]);path.add(nums[i]);backTracking(nums, i + 1);path.remove(path.size() - 1);}}
}

---

46. 全排列

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

示例 1：

• 输入：nums = [1,2,3]
• 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

示例 2：

• 输入：nums = [0,1]
• 输出：[[0,1],[1,0]]

示例 3：

• 输入：nums = [1]
• 输出：[[1]]

提示：

• 1 <= nums.length <= 6
• -10 <= nums[i] <= 10
• nums 中的所有整数 互不相同

解题思路

典型的排列问题，回溯搜索代替for来暴力实现

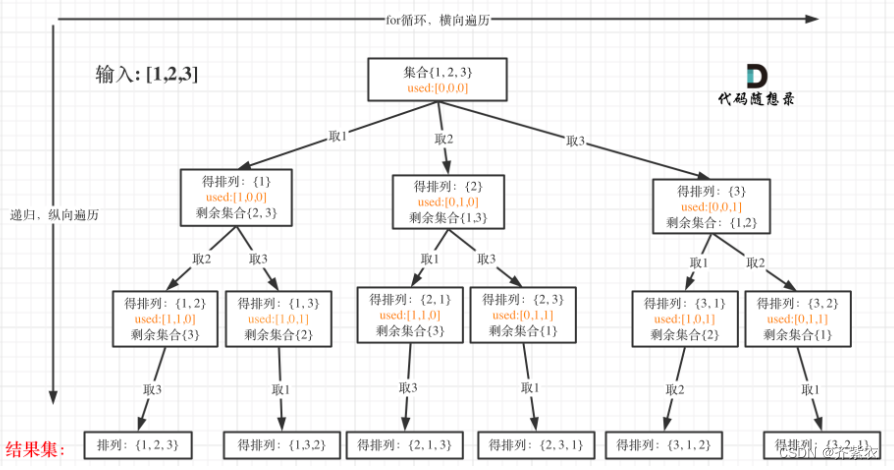
源码

class Solution {List<List<Integer>> result = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();boolean[] used;public List<List<Integer>> permute(int[] nums) {if (nums.length == 0){return result;}used = new boolean[nums.length];permuteHelper(nums);return result;}private void permuteHelper(int[] nums){if (path.size() == nums.length){result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++){if (used[i]){continue;}used[i] = true;path.add(nums[i]);permuteHelper(nums);path.removeLast();used[i] = false;}}
}

---

47. 全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序 返回所有不重复的全排列。

示例 1：

• 输入：nums = [1,1,2]
• 输出：
  [[1,1,2],
  [1,2,1],
  [2,1,1]]

示例 2：

• 输入：nums = [1,2,3]
• 输出：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

提示：

• 1 <= nums.length <= 8
• -10 <= nums[i] <= 10

解题思路

这道题目和46.全排列 的区别在与给定一个可包含重复数字的序列，要返回所有不重复的全排列。

这里又涉及到去重了。

在40.组合总和II 、90.子集II 我们分别详细讲解了组合问题和子集问题如何去重。

那么排列问题其实也是一样的套路。

还要强调的是去重一定要对元素进行排序，这样我们才方便通过相邻的节点来判断是否重复使用了。

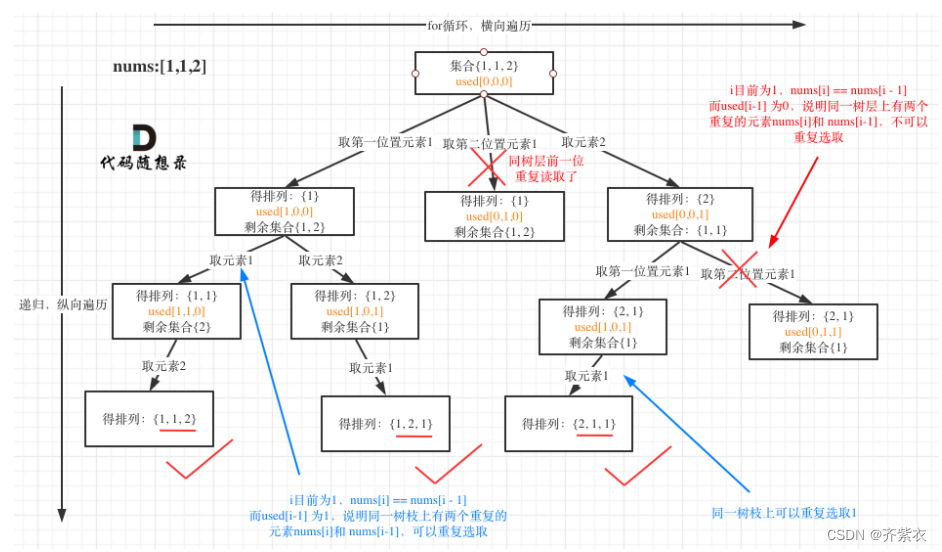
源码

class Solution {List<List<Integer>> result = new ArrayList<>();List<Integer> path = new ArrayList<>();public List<List<Integer>> permuteUnique(int[] nums) {boolean[] used = new boolean[nums.length];Arrays.fill(used, false);Arrays.sort(nums);backTrack(nums, used);return result;}private void backTrack(int[] nums, boolean[] used) {if (path.size() == nums.length) {result.add(new ArrayList<>(path));return;}for (int i = 0; i < nums.length; i++) {if (i > 0 && nums[i] == nums[i - 1] && used[i - 1] == false) {continue;}if (used[i] == false) {used[i] = true;path.add(nums[i]);backTrack(nums, used);path.remove(path.size() - 1);used[i] = false;}}}
}

---

总结

这篇关于代码随想录算法训练营第二十九天（回溯5）|491. 非递减子序列、46. 全排列、47. 全排列 II(JAVA)的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---