搜索最短路/最小步数问题

本文主要是介绍搜索最短路/最小步数问题，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

搜索专题之最短路/最小步数

迷宫问题

【题目描述】

【输入样例】

5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

【输出样例】

0 0
1 0
2 0
2 1
2 2
2 3
2 4
3 4
4 4

【AC代码】

#include <iostream>
#include <cstring>#define x first 
#define y second
using namespace std;
const int N = 1010, M = N * N;
typedef pair<int, int> PII;
int g[N][N];
PII q[M];
PII pre[N][N];
int n;
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};void bfs(int sx, int sy) {memset(pre, -1, sizeof pre);int hh = 0, tt = -1;q[++ tt] = {sx, sy};pre[sx][sy] = {0, 0};	//这里随意标记下被遍历过了 while(hh <= tt) {PII t = q[hh ++];for(int i = 0; i < 4; i ++) {int a = t.x + dx[i], b = t.y + dy[i];if(a < 0 || a >= n || b < 0 || b >= n || g[a][b])	continue;if(pre[a][b].x != -1)	continue;q[++ tt] = {a, b};pre[a][b] = t;}}}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ )for (int j = 0; j < n; j ++ )scanf("%d", &g[i][j]);bfs(n - 1, n - 1);PII end(0, 0);while (true){printf("%d %d\n", end.x, end.y);if (end.x == n - 1 && end.y == n - 1) break;end = pre[end.x][end.y];}return 0;
}

---

武士风度的牛

【题目描述】

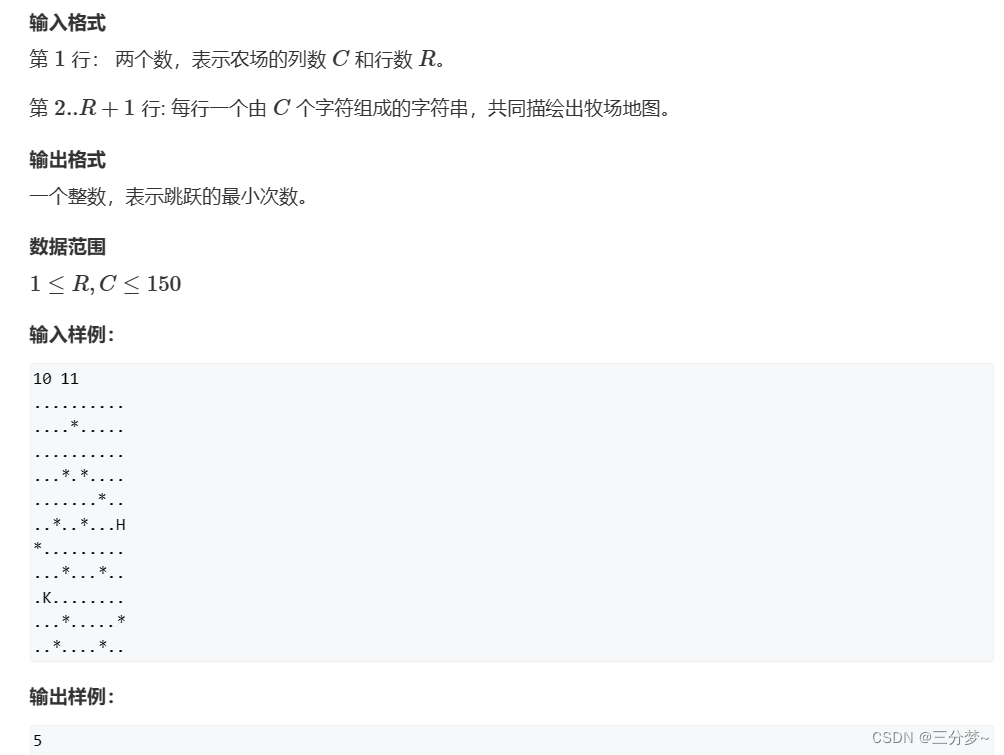
【AC代码】

#include <iostream>
#include <cstring>#define x first
#define y second
using namespace std;
const int N = 160, M = N * N;
typedef pair<int, int> PII; 
char g[N][N];
int dist[N][N];
int m, n;
PII q[M];int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};int bfs(PII start, PII end) {int hh = 0, tt = -1;memset(dist, -1, sizeof dist);q[++ tt] = start;dist[start.x][start.y] = 0;while(hh <= tt) {PII t = q[hh ++];for(int i = 0; i < 8; i ++) {int a = t.x + dx[i], b = t.y + dy[i];if(a < 0 || a >= n || b < 0 || b >= m)	continue;if(g[a][b] == '*')	continue;if(dist[a][b] != -1)	continue;dist[a][b] = dist[t.x][t.y] + 1;q[++ tt] = {a, b};if(make_pair(a, b) == end)  return dist[a][b];}}return -1;
}int main() {cin >> m >> n;for(int i = 0; i < n; i ++)	scanf("%s", &g[i]);PII start, end;for(int i = 0; i < n; i ++)for(int j = 0; j < m; j ++) {if(g[i][j] == 'K')start = make_pair(i, j);if(g[i][j] == 'H')end = make_pair(i, j);}cout << bfs(start, end) << endl;return 0;
}

---

抓住那头牛

【题目描述】

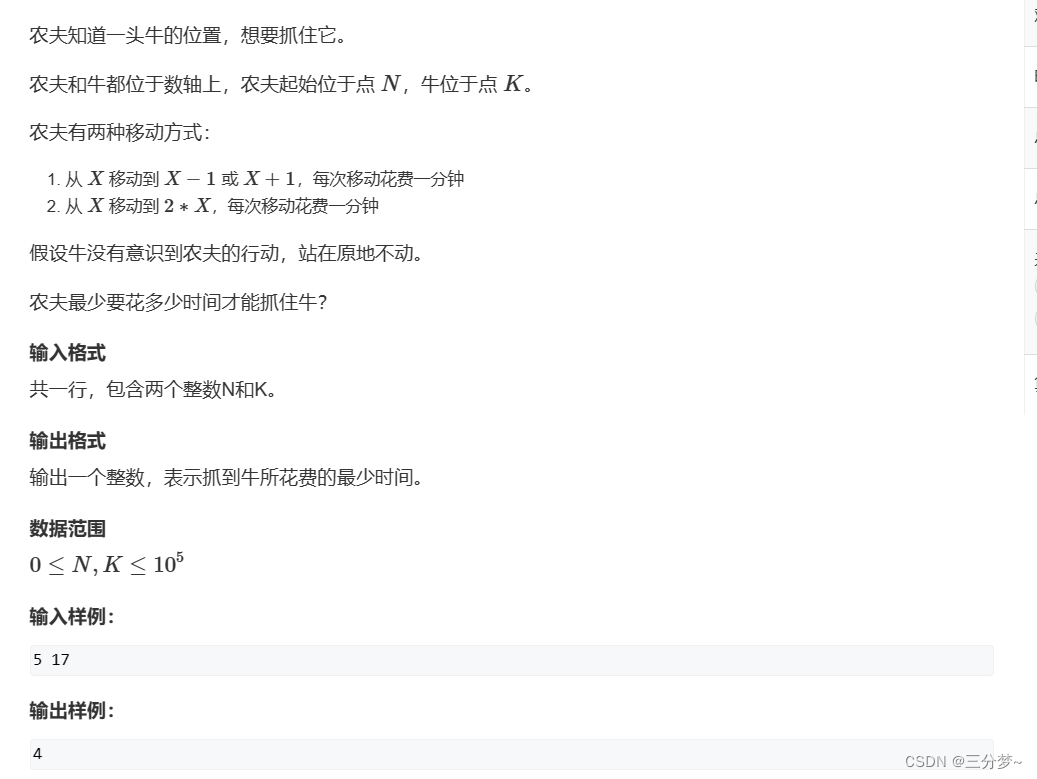
【AC代码】

#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e5 + 10;
int dist[N];
int q[N];
int n, k;int bfs() {memset(dist, -1, sizeof dist);int hh = 0, tt = -1;q[++ tt] = n;	//起点入队列dist[n] = 0;    //起点到起点为0while(hh <= tt) {int t = q[hh ++];if(t == k)	return dist[t];//三种走法遍历// x + 1if(t + 1 < N && dist[t + 1] == -1) {dist[t + 1] = dist[t] + 1;q[++ tt] = t + 1;} //x - 1if(t - 1 >= 0 && dist[t - 1] == -1) {dist[t - 1] = dist[t] + 1;q[++ tt] = t - 1;}//x * 2if(t * 2 < N && dist[t * 2] == -1) {dist[t * 2] = dist[t] + 1;q[++ tt] = t * 2;}} return -1;
}int main() {cin >> n >> k;cout << bfs() << endl;return 0;
}

---

魔板

【题目描述】

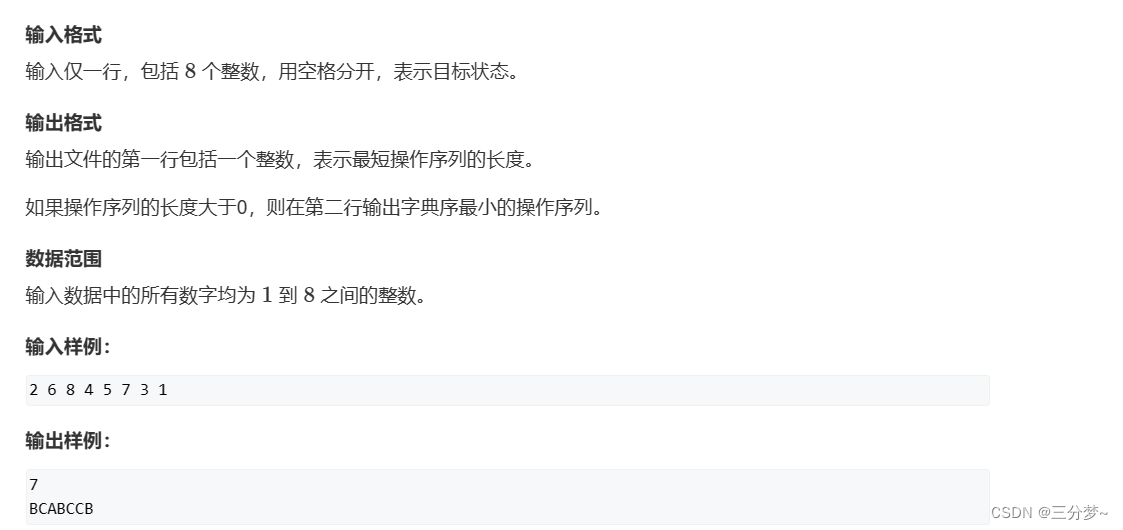
【AC代码】

#include <cstring> // 引入cstring头文件，用于字符串操作
#include <iostream> // 引入iostream头文件，用于输入输出流操作
#include <algorithm> // 引入algorithm头文件，用于算法操作
#include <unordered_map> // 引入unordered_map头文件，用于哈希映射操作
#include <queue> // 引入queue头文件，用于队列操作using namespace std;char g[2][4]; // 定义一个二维字符数组g，表示状态
unordered_map<string, pair<char, string>> pre; // 定义一个哈希映射pre，存储状态的前驱和移动方式
unordered_map<string, int> dist; // 定义一个哈希映射dist，存储状态的最短距离void set(string state)
{for (int i = 0; i < 4; i ++ ) g[0][i] = state[i]; // 将状态的前四个字符赋值给g的第一行for (int i = 7, j = 0; j < 4; i --, j ++ ) g[1][j] = state[i]; // 将状态的后四个字符赋值给g的第二行
}string get()
{string res;for (int i = 0; i < 4; i ++ ) res += g[0][i]; // 将g的第一行字符拼接成字符串for (int i = 3; i >= 0; i -- ) res += g[1][i]; // 将g的第二行字符逆序拼接成字符串return res;
}string move0(string state)
{set(state);for (int i = 0; i < 4; i ++ ) swap(g[0][i], g[1][i]); // 交换g的第一行和第二行的字符return get();
}string move1(string state)
{set(state);int v0 = g[0][3], v1 = g[1][3]; // 保存g的第一行和第二行的最后一个字符for (int i = 3; i > 0; i -- ){g[0][i] = g[0][i - 1]; // 将g的第一行字符向右移动一位g[1][i] = g[1][i - 1]; // 将g的第二行字符向右移动一位}g[0][0] = v0, g[1][0] = v1; // 将保存的字符放到g的第一行和第二行的第一个位置return get();
}string move2(string state)
{set(state);int v = g[0][1]; // 保存g的第一行的第二个字符g[0][1] = g[1][1]; // 将g的第二行的第二个字符赋值给g的第一行的第二个字符g[1][1] = g[1][2]; // 将g的第二行的第三个字符赋值给g的第二行的第二个字符g[1][2] = g[0][2]; // 将g的第一行的第三个字符赋值给g的第二行的第三个字符g[0][2] = v; // 将保存的字符放到g的第一行的第三个位置return get();
}int bfs(string start, string end)
{if (start == end) return 0; // 如果起始状态和目标状态相同，返回0queue<string> q; // 定义一个队列q，用于广度优先搜索q.push(start); // 将起始状态加入队列dist[start] = 0; // 起始状态的最短距离为0while (!q.empty()){auto t = q.front(); // 取出队列的第一个元素q.pop(); // 弹出队列的第一个元素string m[3]; // 定义一个字符串数组m，存储移动后的状态m[0] = move0(t); // 将t进行move0操作得到移动后的状态m[0]m[1] = move1(t); // 将t进行move1操作得到移动后的状态m[1]m[2] = move2(t); // 将t进行move2操作得到移动后的状态m[2]for (int i = 0; i < 3; i ++ )if (!dist.count(m[i])) // 如果状态m[i]不在dist中{dist[m[i]] = dist[t] + 1; // 更新状态m[i]的最短距离pre[m[i]] = {'A' + i, t}; // 更新状态m[i]的前驱和移动方式q.push(m[i]); // 将状态m[i]加入队列if (m[i] == end) return dist[end]; // 如果状态m[i]等于目标状态，返回最短距离}}return -1; // 如果无法到达目标状态，返回-1
}int main()
{int x;string start, end;for (int i = 0; i < 8; i ++ ){cin >> x; // 输入一个整数xend += char(x + '0'); // 将x转换为字符并添加到end字符串末尾}for (int i = 1; i <= 8; i ++ ) start += char('0' + i); // 初始化start字符串为"12345678"int step = bfs(start, end); // 进行广度优先搜索，得到最短步数cout << step << endl; // 输出最短步数// 有pre反推出变换序列string res;while (end != start){res += pre[end].first; // 将当前状态的移动方式添加到res字符串末尾end = pre[end].second; // 更新当前状态为前驱状态}reverse(res.begin(), res.end()); // 将res字符串逆序if (step > 0) cout << res << endl; // 如果存在最短路径，输出移动方式return 0;
}

这篇关于搜索最短路/最小步数问题的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---